Круговые процессы. Цикл Карно
Круговым является тепловой процесс, при котором термодинамическая система, пройдя ряд состояний, возвращается в исходное. Графически круговой процесс изображается замкнутой кривой 1-а-2-в-1 (рис. 6.1.).
 Если круговой процесс может протекать сначала в прямом (1-а-2-в-1), а потом в обратном направлении (1-в-2-а-1), то он является обратимым. При этом в окружающей среде и в самой системе не происходит никаких изменений. В противоположном случае процесс является необратимым.
Если круговой процесс может протекать сначала в прямом (1-а-2-в-1), а потом в обратном направлении (1-в-2-а-1), то он является обратимым. При этом в окружающей среде и в самой системе не происходит никаких изменений. В противоположном случае процесс является необратимым.
Работа кругового цикла 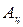 определяется площадью, заштрихованной на рис. (6.1) фигуры, причем:
определяется площадью, заштрихованной на рис. (6.1) фигуры, причем:
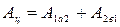 .
.
При круговом процессе изменение внутренней энергии 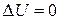 . Поэтому
. Поэтому
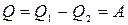 ;
;
где: 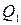 - количество теплоты, полученное термодинамической системой;
- количество теплоты, полученное термодинамической системой; 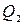 - количество теплоты, отданное системой в процессе.
- количество теплоты, отданное системой в процессе.
Коэффициент полезного действия кругового процесса:
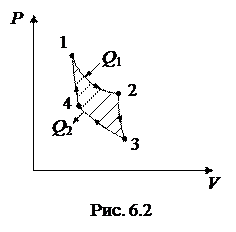
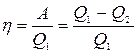 (6.1)
(6.1)
Наиболее экономичным является круговой цикл, состоящий из 2-х изотерм (расширения 1-2 при Т1 и сжатия 3-4 при Т2) и 2-х адиабат (расширения 2-3 и сжатия 4-1). Такой цикл называется циклом Карно (рис. 6.2).
Для такого цикла к.п.д. не зависит от химической природы рабочего тела, а определяется только температурами Т1 и Т2, т.е.
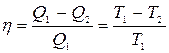 (6.2)
(6.2)
Прямой и обратный циклы Карно лежат в основе действия тепловых и холодильных машин.
ЭНТРОПИЯ. II И III НАЧАЛА ТЕРМОДИНАМИКИ
Если термодинамическая система получает количество теплоты, то меняется ее состояние, которое можно характеризовать некоторой функцией. Такой функцией является энтропия S. Энтропия не зависит от того, каким образом система пришла в данное состояние и является мерой неупорядоченности системы. Любой тепловой процесс в замкнутой термодинамической системе происходит так, что энтропия не уменьшается, т.е
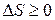 . (7.1)
. (7.1)
Количественно величина изменения энтропии на малом участке процесса определяется отношением количества теплоты dQ, полученного системой, к температуре теплоотдающего тела T:
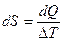 . (7.2)
. (7.2)
При переходе системы из состояния 1 в состояние 2 изменение энтропии равно:
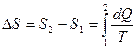 . (7.3)
. (7.3)
Используя первый закон термодинамики (5.4); выражения для ∆U (5.1а) и работы А (5.3), выражение (7.3) можно привести к виду:
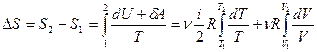 . (7.4)
. (7.4)
Для изопроцессов:
1) 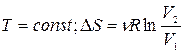 - изотермический;
- изотермический;
2) 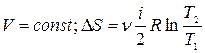 - изохорический
- изохорический
3) 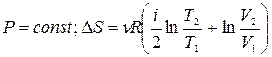 - изобарический
- изобарический
4) 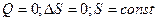 - адиабатический или изоэнтропийный.
- адиабатический или изоэнтропийный.
С помощью понятия энтропии формулируются II и III законы термодинамики:
"Любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает".
"Энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к нулю Кельвина":
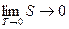 (7.5)
(7.5)
