Задание 1. Определение момента инерции маятника Обербека

Вывод расчетной формулы

Рассмотрим маховик (рис.7), состоящий из диска, шкива и вала. Предположим, что они обладают общей массой М. Диск и шкив насажены на общий вал, закрепленный в подшипниках. Маховик может вращаться относительно оси z, совпадающей с осью вала (на рис. 7 ось z перпендикулярна плоскости чертежа и направлена «от нас»).

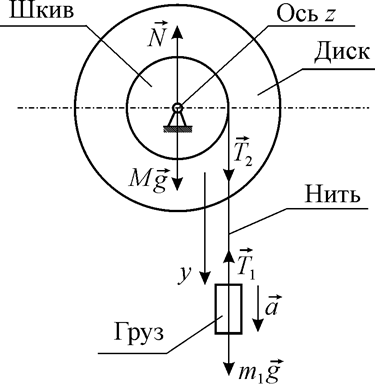
Рис.7.

Схема системы маховик-груз (вал на схеме не показан)

Вращение маховика осуществляется под действием груза массой m₁, укрепленного на нити, намотанной на шкив, и описывается относительно неподвижной оси z уравнением:

,

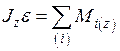(20)

где 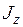- момент инерции маховика, 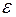– его угловое ускорение, – сумма моментов сил, действующих на маховик. включает момент силы натяжения нити М(Т₂) и момент силы трения М(F_тр) в подшипниках вала. Моменты сил N и Мg относительно оси z равны нулю. Таким образом,

.

(21)

Поступательное движение груза массой m₁ описывается вторым законом Ньютона:

,

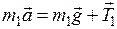(22)

где а - ускорение центра масс груза, Т₁ – сила натяжения нити, приложенной к грузу. В проекции на ось у уравнение (22) принимает вид:

(23)

Так как предполагается, что нить нерастяжима и невесома, то ускорение всех точек нити и груза одинаковы, причем в отсутствии проскальзывания нити линейное (тангенциальное) ускорение обода диска равно ускорению груза. Силы натяжения нити Т₁ и Т₂ равны между собой (Т₁ = Т₂ = Т).

Предположим, что груз в процессе движения всей системы опускается до некоторого нулевого уровня с высоты h₁. Тогда с учетом, что

,

(24)

где t - время движения груза, а

;

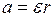(25)

имеем

.

(26)

где x = r = R.

Из уравнения (21), находим

.

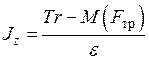(27)

Силу натяжения Т выражаем из уравнения (23), а угловое ускорение e – из (26). Затем полученные формулы для Т и e подставляем в (27). В итоге получаем,

.

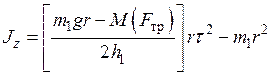(28)

Для расчета 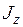нужно знать все величины, входящие в формулу (28). Они определяются экспериментально: 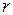– с помощью штангенциркуля, 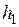– с помощью линейки, t – с помощью секундомера. Масса груза m₁ изначально задана. Момент силы трения 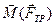определяется экспериментальным путем путем.

Пусть I – момент инерции маятника Обербека без грузов. Из (26) следует, что

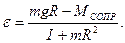(29)

В условиях эксперимента mR² << I , что позволяет считать зависимость ε(m) линейной.

Эту зависимость можно использовать для экспериментальной оценки величины М_СОПР. Действительно, если полученную экспериментально зависимость ε(m) экстраполировать² до пересечения с осью абсцисс, то есть до точки m₀ на этой оси, для которой выполняется равенство , то это позволяет определить М_СОПР как

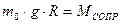(30)

Для определения момента инерции маятника I воспользуемся формулой (28), где величина М_СОПР предварительно определена из измерений ε(m) и формулы (30). Подставив выражение ε из (26) и М_СОПР из (30) в (28), получаем рабочую формулу для определения момента инерции маятника

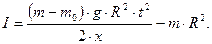(31)

Для используемого в работе маятника Обербека справедливо неравенство 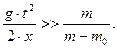Учитывая это, получаем:

Для расчетов удобно представить момент инерции в виде:

(32)

где

Таким образом, для определения момента инерции маятника необходимо измерить время t опускания груза массой m на расстояние x .

Зависимость момента инерции маятника от расстояния грузов до оси вращения предполагается проверить, используя результаты, полученные по формуле (32). Значение т₀ можно взять из данных эксперимента для определения момента инерции маятника Обербека без грузов, считая, что момент сил сопротивления остается постоянным.

²экстраполировать - статистические данные или результаты серии экспериментов. Отмечаем их в виде точек на графике, как значения от какого-то аргумента. Если теперь попытаться вычислить такую функцию, которая бы описывала этот график, это мы будем апроксимировать его. Функция может точно через эти точки не пройти, потому что всегда есть погрешности. Если мы будем вычислять точное значение ещё не отмеченной точки (например, при данном аргументе измерение не проводилось) по уже имеющимся - это мы интерполируем (от латинского "интер" - между). А если мы примемся расширять область аргумента - вот это и будет экстраполяция (от латинского "экстра" - вне).