Статика. Статика жидкостей и газов
1. Условием равновесия тел является равенство нулю суммы всех сил, действующих на тело, т.е.

2. Тело, имеющее ось вращения, находится в равновесии, если сумма моментов внешних сил относительно этой оси равна нулю:
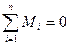
Момент силы  , где l - кратчайшее расстояние от оси вращения до линии действия силы (плечо). Момент силы, стремящийся повернуть тело относительно оси, против часовой стрелки считается положительным, по часовой стрелке – отрицательным.
, где l - кратчайшее расстояние от оси вращения до линии действия силы (плечо). Момент силы, стремящийся повернуть тело относительно оси, против часовой стрелки считается положительным, по часовой стрелке – отрицательным.
3. Давлением называется величина силы, действующей на единицу площади поверхности перпендикулярно к ней:

Давление столба жидкости высотой h:
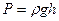
где 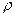 - плотность жидкости.
- плотность жидкости.
- По закону Архимеда, выталкивающая сила, действующая на тело, погруженное в жидкость или газ:

где 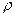 - плотность жидкости, V- объем, погруженной части тела.
- плотность жидкости, V- объем, погруженной части тела.
Пример 18.
Труба массой 50 кг лежит на земле. Какую минимальную силу нужно приложить, чтобы приподнять трубу за один конец?
Решение.
Ось вращения трубы находится в точке О, на конце трубы. Неизвестная сила приложена к другому концу, сила тяжести к центру. По правилу моментов получаем:
Момент силы тяжести должен быть равен моменту приложенной силы, т.е.

Откуда следует:

Пример 19.
Однородное тело плавает на поверхности керосина так, что объем погруженной части составляет 0,92 всего объема тела. Определить объем погруженной части при плавании тела на поверхности воды.
Решение.
На тело, плавающее в керосине, действует сила тяжести и выталкивающая сила керосина. Тогда, из условия плавания:
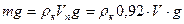 , где
, где 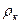 - плотность керосина.
- плотность керосина.
Аналогично, запишем условие плавания тел в воде:
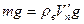 , где
, где  - плотность воды.
- плотность воды.
Тогда, из этих уравнений получим:

Откуда
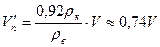
 Молекулярная физика и термодинамика
Молекулярная физика и термодинамика
- Идеальные газы подчиняются уравнению Клапейрона-Менделеева:

где 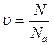 - количество вещества однородного газа (в молях) или
- количество вещества однородного газа (в молях) или 
R – универсальная газовая постоянная;
Т – термодинамическая температура Кельвина;
N- число молекул газа;
Na – число Авогадро;
m – масса газа;
m - молярная масса газа.
Если система представляет смесь нескольких газов, то количество вещества системы:
 или
или 
Молярная масса смеси газов: 
где ui, Ni, mi, mi - соответственно количество вещества, число молекул, масса, молярная масса i–й компоненты смеси.
2. Газовые законы для изопроцессов:
Закон Бойля-Мариотта для изотермического процесса (Т = const; m = const):
pV = const, или P1V1 = P2V2,
Закон Гей-Люссака для изобарического процесса (р = const, m = const):
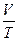 = const, или
= const, или 
Закон Шарля для изохорического процесса (V = const, m = const):
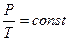 или
или 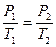
Уравнение Пуассона, связывающие параметры идеального газа при адиабатическом процессе:
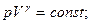
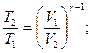
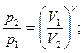

Объединенный газовый закон (m = const):
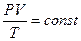 или
или 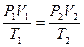
3. Закон Дальтона, определяющий давление смеси газов:
P = P1 + P2 + …Pn,
где Рi – парциальные давления компонент смеси; n – число компонентов смеси.
4. Основное уравнение кинетической теории газов:

где Wк – средняя кинетическая энергия поступательного движения молекулы:

n- концентрация молекул:

N - число молекул, содержащихся в данной системе;
r - плотность вещества.
k =1,38∙1023 Дж/К – постоянная Больцмана.
5. Средняя полная кинетическая энергия молекулы: 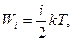
где i – число степеней свободы молекулы.
Скорость молекул (mi - масса одной молекулы)
| Скорость молекул | формула |
| средняя квадратичная | 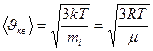 |
| средняя арифметическая | 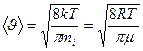 |
| наиболее вероятная |  |
6. Первое начало термодинамики:
Q = DU + A,
где Q – теплота, сообщенная системе (газу);
DU - изменение внутренней энергии системы;
А – работа, совершенная системой против внешних сил.
Работа расширения газа
| Процесс | Формула работы расширения газа |
| в общем случае |  |
| при изобарическом процессе | A = P(V2 – V1) |
| при изотермическом процессе | 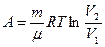 |
| при адиабатическом процессе | 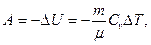 или или  где g = Cp/Cv – показатель адиабаты. где g = Cp/Cv – показатель адиабаты. |
| при изохорическом процессе |
7. Внутренняя энергия идеального газа:

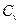 -удельная теплоемкость газа при постоянном объеме:
-удельная теплоемкость газа при постоянном объеме:
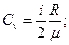
и при постоянном давлении 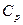 :
:
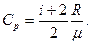
Уравнение Майера:
Ср – Сv = R.
8. Связь между удельной с и молярной С теплоемкостями
с = С/m или С = сm
9. КПД цикла:
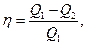
где Q1 – теплота, полученная рабочим телом от нагревателя;
Q2 - теплота, переданная рабочим телом охладителю.
КПД цикла Карно:
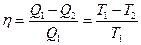 ,
,
где Т1 и Т2 – температуры нагревателя и охладителя.
10. Коэффициент поверхностного натяжения:
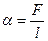 , или
, или 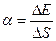
где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости;
DЕ – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади DS
11. Добавочное давление р, вызванное кривизной жидкостивыражается
формулой Лапласа:

где R1 и R2 – радиусы двух любых взаимно перпендикулярных сечений поверхности;
Давление, создаваемое сферической поверхностью жидкости:
p = 2a/R,
где R – радиус сферической поверхности.
12. Высота подъема жидкости в капиллярной трубке:
 ,
,
где q – краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном несмачивании);
R- радиус канала трубки;
r - плотность жидкости;
g - ускорение свободного падения.
Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями:
 ,
,
где d – расстояние между плоскостями.
Пример 20.
В баллоне находилось m1=2кг газа при давлении 10МПа. Какое количество газа израсходовано, если давление стало 2МПа. Температура газа постоянна.
Решение.
По уравнению Менделеева-Клапейрона для начального и конечного состояний можно написать:
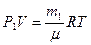

Разделив одно уравнение на другое, получим:
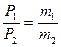
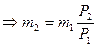
Масса израсходованного газа:
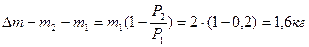
Пример 21.
В сосуде находится 14г азота и 19г водорода при давлении 100кПа и температуре 27°с. Найти объем сосуда. Молярная масса азота 0,028 кг/моль, водорода 0,002кг/моль.
Решение.
Давление газа в сосуде создается азотом и водородом. По закону Дальтона:
P=P1+P2
Из уравнения состояния давление каждого газа:


Тогда 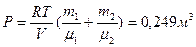
Пример 22.
Два моля одноатомного газа нагреваются при постоянном объеме до температуры 450К. На сколько изменилась внутренняя энергия газа, если давление увеличилось в 3 раза?
Решение.
Для изохорического процесса
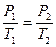
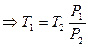
Изменение внутренней энергии газа
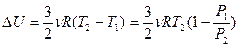
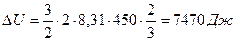
Пример 23.
Какую работу против сил поверхностного натяжения надо совершить, чтобы выдуть мыльный пузырь радиусом 0,05 м? Чему равно избыточное давление внутри мыльного пузыря?
Решение.
1) Совершаемая при выдувании пузыря работа против сил поверхностного натяжения идет на увеличение поверхностной энергии DЕ. Увеличение поверхности жидкости на DS связано с приростом поверхностной энергии DЕ:
DE = sDS
Мыльный пузырь представляет собой очень тонкую пленку мыльной воды приблизительно сферической формы. Эта пленка имеет две поверхности – наружную и внутреннюю. Пренебрегая толщиной пленки и считая поэтому радиусы обеих сфер одинаковыми, найдем их общую площадь:
S = 4pR2 + 4pR2 = 8pR2 

Тогда
A = DE = 8pR2s
2) Для определения избыточного давления внутри пузыря учтем, что каждая из двух сферических поверхностей пузыря – наружная и внутренняя – производит вследствие своей кривизны давление на воздух внутри пузыря. Это давление, производимое каждой сферой, можно найти по формуле Лапласа, имея в виду, что радиусы кривизны всех нормальных сечений для сферы равны ее радиусу, следовательно, R1 = R2 = R. Избыточное давление воздуха внутри пузыря равно:
Dp = 2 pпов = 4s/R
Взяв из таблицы значения s для мыльной воды s = 40×10-3 Н/м и выполнив вычисление получим:
А = 2,5 × 10-3 Дж = 2,5 мДж; Dр = 3,2 Па.
