Уравнение Клаузиуса — Мосотти для неполярных газов и жидкостей
Между диэлектрической проницаемостью и поляризуемостью молекул существует определенное соотношение, называемое уравнением Клаузиуса — Мосотти.
Индуцированные электрические моменты молекул неполярного газа или жидкости одинаковы у всех молекул однородного по составу диэлектрика. Индуцированный момент пропорционален напряженности действующего на молекулу поля:

где α — поляризуемость молекулы, которая считается одинаковой для всех молекул.
Поляризация, т. е. электрический момент единицы объема, равна
 ,
,
где п — число молекул в единице объема.
Локальное поле связано с напряженностью среднего поля соотношением , так что
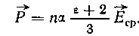 .
.
С другой стороны, между поляризацией и средним полем существует соотношение .
Исключив Р и Е из соотношений и , получим уравнение Клаузиуса — Мосотти для диэлектрической проницаемости неполярных газов и жидкостей
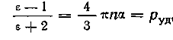 ,
,
где pуд обозначена величина, называемая удельной поляризацией.
Уравнение Клаузиуса-Мосотти можно представить и в другой форме. Для этого умножим обе части уравнения на граммолекулярный объем, который равен отношению M/ρ, где M - молекулярный вес, а ρ - плотность,
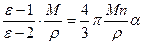 .
.
Отношение n/ρ есть 1/m, где m - масса молекулы; отношение M/m представляет собой число Авогадро N = 6,06×1023. Следовательно,
 ,
,
где РM — молекулярная поляризация.
Для неполярных газов и жидкостей величина РM близка к величине молекулярной рефракции PR
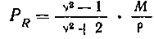 .
.
Действительно, согласно электромагнитной теории света Максвелла показатель преломления света
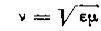 ,
,
где μ — магнитная проницаемость газов.
Магнитная проницаемость всех веществ, за исключением ферромагнетиков, как известно, близка к единице. Поэтому 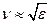 или
или  .
.
Расхождение между ε и n2 объясняется тем, что при частотах электромагнитного поля, равных частоте света, не успевает образоваться поляризация, связанная со смещением ядер. Этот вид поляризации устанавливается при частотах порядка 1012 —1013 гц и ниже, и, следовательно, ε должна быть несколько больше, чем n2 из-за присутствия ядерной поляризации. Однако величина поляризации ядерного смещения очень невелика, так что можно считать, что для неполярных газов и жидкостей ε в первом приближении равна n2 и молекулярная поляризация равна молекулярной рефракции.
Уравнение Клаузиуса—Мосотти справедливо, когда на молекулу действует локальное поле, определяемое выражением .
Уравнение для неполярных газов можно упростить. Для таких газов значение ε близко к единице. Поэтому в знаменателе формулы можно принять, что ε = 1. Тогда получим
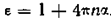 .
.
Это уравнение справедливо только в случае малых диэлектрических проницаемостей, т. е. для газов.
