Механические колебания и волны

Вариант 1	Вариант 2
1. Что называется фазой гармонического колебания?	1. Что называется длиной волны, волновым числом?
2. Какова разность фаз двух маятников (второго относительно первого) (см. рисунок)?	2. Какова разность фаз двух маятников (второго относительно первого) (см. рисунок)?
1 2 Крайнее положние	1 2
3. Точка участвует в двух взаимно перпендикулярных колебаниях. Какая фигура Лиссажу y(x) получается, если	3. Точка участвует в двух взаимно перпендикулярных колебаниях. Какая фигура Лиссажу y(х) получается, если
4. Сложите графически два гармонических одинаково направленных колебания равных периодов, но смещенных по фазе относительно друг друга на p, амплитуды соотносятся как 3 : 1. Будет ли колебание гармоническим? Чему равна частота сложного колебания?	4. Сложите графически два гармонических одинаково направленных колебания, у которых частоты соотносятся как 1 : 3, а амплитуды как 2 : 1. Будет ли колебание гармоническим? Чему равна частота сложного колебания?
5. Дано направление смещения частиц. Куда движется волна (влево, вправо)?	5. Дано направление смещения частиц. Куда движется волна (влево, вправо)
6. Написать дифференциальное уравнение затухающих колебаний и его решение. Каков смысл коэффициента затухания, добротности?	6. Написать волновое уравнение. Пояснить его смысл
7. Дано уравнение волны Y = A × sin2p(t/T-x/l), где A, T, l – положительные величины, которые описывают волну. Чему равна скорость волны?	7. Смещение частиц среды в плоской бегущей звуковой волне выражается соотношением x = xm × сos(wt – kx). Найти скорость смещения частиц в этой волне.
8. Что такое фазовая скорость, групповая скорость волн?	8. Как образуется стоячая волна? Описать её характерные особенности. Написать уравнение стоячей волны.
9. Что называется интерференцией волн?	9. Как образуются биения?
10. Период колебаний пружинного маятника равен Т. Массу маятника увеличили в 4 раза. Как изменится период колебаний?	10. Что называется механическим резонансом, резонансной частотой?

ЗАДАЧИ

1. МЕХАНИКА

Кинематика

Примеры решения задач

1. Радиус-вектор частицы изменяется со временем по закону 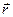= t³ +3t² (м), где, орты осей x и y. Определить для момента времени t = 1 c:

а) модуль скорости;

б) модуль ускорения.

Дано: 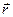= t3 +3t2 t = 1 с.	Решение Вектор скорости определяем как первую производную радиус-вектора по времени. = = 3 + 6t .
υ = ? = ?

В то же время вектор скорости, как и любой вектор можно представить через его компоненты = υ_x + υ_y + υ_z .

Сравнивая это выражение с предыдущим, получим: υ_x = 3 ; υ_y = 6t; υ_z = 0.

Модуль скорости определяется через компоненты:

м/с.

Ускорение частицы равно производной от вектора скорости

, где компоненты W_x = 6t, W_y = 6.

Модуль ускорения

= 8,48 м/c² ≈ 8,5 м/c².

Ответ: 1) = 6,7 м/c;

2) W = 8,5 м/c².

2. Точка движется в плоскости xy из положения с координатами х₁ = у₁ = 0 со скоростью = a +bx (a; b – постоянные, ; – орты осей и х и у)

Определите: 1) уравнение траектории точки у(х); 2) форму траектории.

Дано: х1 = у1 = 0 = a x+bx y	Решение: Компоненты скорости υx = а, υу = bx . Так как υx = , a υ = (х и у – компоненты радиус-вектора) = а; = bx.
1) y(x) = ? 2) форма траектории?

Из последних выражений, исключая время, получаем или . Интегрируя, получим . Траектория является параболой.

Ответ: 1) у = ; 2) парабола.

3. Частица движется по окружности радиусом м, и путь изменяется со временем по закону , где м/с³. Найти: а) момент времени , при котором нормальное ускорение будет равно тангенциальному ; б) полное ускорение в этот момент времени.

Дано: м м/с³	Решение   а) Выражения для нормального, тангенциального и полного ускорений имеют вид: Wn = ; Wr = ; Из условия задачи получим уравнение относительно t0: или . Отсюда для t0 имеем: с;
a) б)

б) для полного ускорения из условия задачи получим

м/с² м/с².

Ответ: t₀ = 0,87 с, W = 15 м/с².

4. Тело брошено с вышки в горизонтальном направлении со скоростью = 30 м/с. Найти значения следующих величин через две секунды τ = 2,0 с: а) скорости 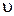, тангенциального ускорения W_τ, нормального ускорения W_n; б) радиуса кривизны траектории R.

Дано: 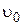= 30 м/с τ = 2,0 с	Решение Траектория движения тела показана на рисунке. Направление вектора , составляющих скорости , , а также , , через время τ также показано на рисунке.
а) , Wτ, Wn –? б) R –?

Введем систему координат XOY, как показано на рисунке, чтобы учесть независимость движений тела по горизонтали и вертикали. Проекция вектора скорости на ось OX остается всегда постоянной и равной 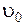. Проекция вектора скорости на ось OY растет со временем по закону = gt, так как вдоль оси OY тело движется равноускоренно с ускорением свободного падения g. Поэтому для модуля скорости тела получим

. (1)

Через две секунды значение модуля скорости будет равно:

м/с.

Из рисунка следует, что

, следовательно, значение нормального ускорения

Аналогично

отсюда тангенциальное ускорение

Радиус кривизны из выражения для нормального ускорения

Ответ: 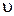= 35,8 м/с; W_τ = 5,4 м/с²; W_n = 8,2 м/с²; R = 1,6 м.

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1.1. Компоненты скорости частицы изменяются со временем по законам: , , u_z = 0, где а и w – константы. Найти модули скорости | | и ускорения , а также угол a между векторами и . По какой траектории движется частица?

(| | = а, = аw, a = p/2)

1.2. Зависимость координат движения частицы от времени имеет вид , , z = 0, где а и w – константы.

а) определить радиус-вектор 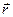, скорость и ускорение частицы, а также их модули;

б) найти уравнение траектории частицы.

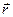( = a(coswt + sinwt ); = a;

= aw (-sinwt +coswt ); | | = aw;

= -aw² (coswt +sinwt ); = aw²;

x²/a² + y²/a² = 1)

1.3. Точка движется по окружности радиусом R = 4 м. Закон ее движения выражается уравнением S = A+Bt², где А = 8 м, В = -2 м/с^2. Определить момент времени t, когда нормальное ускорение W_n точки равно 9 м/с². Найти модули скорости u, тангенциального W_t и полного W ускорения точки в тот же момент времени t.

(t = 1,5 с, u = 6 м/с, W_t= 4 м/с², W = 9,8 м/с²)

1.4. Частица движется со скоростью = at(2 +3 +4 ) (а = 1,0 м/с²). Найти:

а) модуль скорости частицы в момент времени t = 1 с;

б) ускорение частицы и его модуль;

в) путь S, пройденный частицей с момента времени t₁ = 2 с до t₂ = 3 с;

г) какой характер имеет движение частицы? Почему?

(u = 5,4 м/с, = a(2 +3 +4 ), = 5,4 м/с², S = 14 м)

1.5. Точка движется вдоль оси Х, причем координата изменяется по закону . Найти:

а) выражение для проекции на ось Х скорости и ускорения точки;

б) путь S, пройденный точкой за промежуток времени от t = T/8 до t = T/4.

(uх = -(2p/ T) a sin(2p /T) t, Wx = -(2p /T)² a cos (2p/T) t, S = 0,707 a)

1.6. Радиус-вектор частицы изменяется со временем по закону

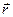= 3t² +2t +1 . Найти:

a) скорость и ускорение частицы;

б) модуль скорости в момент времени t = 1 с;

в) приближенное значение пути S, пройденное частицей за 11-ю секунду движения.

(а) = 6t +2 (м/с); б) = 6 (м/с²); в) | | = 6,3 м/с, S = 63 м).

1.7. Тело брошено под углом a к горизонту и в начальный момент времени имеет скорость . Построить качественные зависимости и как функции от времени движения тела до момента падения. Определить радиус кривизны траектории в момент времени t = t/4, где t – время движения до падения. Сопротивления движению нет.

(R = )

1.8. Тело в течение времени t движется с постоянной скоростью u₀. Затем скорость его линейно нарастает со временем так, что в момент времени 2t она равна 2u₀. Определить путь, пройденный телом за время t. Cчитать что t<t<2t.

(S = + )

1.9. Тoчка движется по криволинейной траектории с постоянным тангенциальным ускорением w_t = 0,5 м/с². Определить полное ускорение точки в момент времени t = 5 с от начала движения, если радиус кривизны траектории в этот момент времени R = 2 м.

(W = 3,2 м/с²)

1.10. Начальное значение скорости = 1 +3 +5 _, (м/с), конечное = 2 +4 +6 _, (м/с). Найти:

а) приращение скорости Δ ; б) модуль приращения скорости | Δ |;

в) приращение модуля скорости u.

(а) Δ = 1 +1 +1 м/с; б) | Δ | = 1,73 м/с, в) u = 1,57 м/с).

1.11. По дуге окружности радиусом R = 10 м движется точка. В некоторый момент времени от начала движения ускорение точки W_n = 5,0 м/с²; вектор полного ускорения образует в этот момент с вектором тангенциального ускорения угол a = 30 . Считая W_t = const, найти закон изменения W_n = f(t).

(W_n = 7,5 t² м/с²).

1.12. Точка движется по дуге окружности радиусом R. Ее скорость зависит от пройденного пути S по закону , где k – постоянная. Найти угол между вектором полного ускорения и вектором скорости в зависимости от S.

( )

1.13. Тело брошено под углом a = 45° к горизонту с начальной скоростью u = 30 м/с. Определить радиус кривизны траектории R в максимальной точке подъема тела и в точке его касания с землей. Качественно постройте зависимости кинетической W_k, потенциальной W_p, и полной W энергии тела как функции времени. Сопротивления движению не учитывать.

(R₁ = 46 м, R₂ = 130 м)

1.14. Материальная точка движется по окружности радиусом R. Ее тангенциальное ускорение изменяется по закону Wt = kt, где k>0. В какой момент времени t с начала движения модули нормального и тангенциального ускорения будут равны? Чему равно полное ускорение материальной точки в этот момент времени? Какой угловой путь j пройдет точка к этому моменту времени? Качественно изобразите закон изменения угловой скорости w как функцию времени.

( ; ; j = 0,67 рад)

1.15. Точка движется по окружности радиусом R = 30 см с постоянным угловым ускорением. Определить тангенциальное ускорение точки, если известно, что с некоторого момента за интервал времени t = 4 с она совершила три оборота и в конце третьего оборота ее нормальное ускорение W_n = 2,7 м/с². Определить угловую w₀ и линейную ₀ скорости в начале указанного интервала времени. Построить графики зависимости модулей ускорения и угловой скорости от времени на интервале движения:

=f(t); W_t = f(t); w = f(t).

(w₀ = 6,4 рад/с; 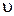₀ = 1,9 м/c)

Динамика

Примеры решения задач

5. Система состоит из частицы 1 массой 1,0 г, расположенной в точке с координатами (1, 1, 1) м, частицы 2 массой 2,0 г, расположенной в точке с координатами (-2, 2, 2) м, частицы 3 массой 3,0 г, расположенной в точке с координатами (-1, 3, -2) м, частицы 4 массой 4,0 г, расположенной в точке с координатами (3, -3, 3) м. Найти радиус – вектор центра масс системы и его модуль.

Дано: m1 = 1,0г m2 = 2,0г m3 = 3,0г m4 = 4,0г = 1 +1 +1 ,м = -2 +2 +2 ,м = -1 + -3 +3 ,м = 3 - 3 +3 ,м	Решение Положение центра масс определяется выражением где mi – масса i-й частицы системы; – радиус-вектор i-й частицы системы. Отсюда для радиус-вектора центра масс рассматриваемой системы, получим
а) – ? б) | | – ?

= , м.

Модуль радиус-вектора центра масс системы

| | = = = 1,27 м.

Ответ: = 0,6 +0,2 +1,1 м; | | = 1,27 м

6. На горизонтальной плоскости лежит доска массой m₁ = 1 кг, а на доске – брусок массой m₂ = 2кг. Коэффициент трения между бруском и доской μ₁ = 0,25, между доской и горизонтальной плоскостью μ₂ = 0,5. С каким ускорением должна двигаться доска, чтобы брусок начал с нее соскальзывать? Какую горизонтальную силу F₀ следует при этом приложить к доске?

Дано: m1 = 1,0 кг m2 = 2,0 кг μ1 = 0,25 μ2 = 0,50	Решение
а) am –? б) F0 –?

Движения доски и бруска одномерные и происходят вдоль оси OX, как показано на рисунке. Поэтому для решения задачи достаточно воспользоваться проекцией уравнения 2-го закона Ньютона на ось OX (как для бруска, так и для доски). Брусок в горизонтальном направлении вынуждает двигаться с ускорением без проскальзования сила трения покоя со стороны поверхности доски. По мере роста ускорения доски растет и величина силы трения покоя. Когда она достигает предельной величины, равной силе трения скольжения F_тр2, брусок начинает соскальзывать с доски. В этом случае из 2-го закона Ньютона получим

m₂W_m = F_тр2 = μ₁F_n2 (1)

где F_n2 – сила нормального давления бруска на поверхность доски.

F_n2 = m₂g. (2)

Из выражений (1) и (2) следует:

W_m = μ₁∙g = 0,25∙9,81 = 2,45 м/с².

На доску действуют в горизонтальной плоскости силы , и , как показано на рисунке. Уравнение движения доски в этом случае имеет вид:

m₁W_m = F_{0 –} F_тр1 – F_тр2, (3)

где F_тр1 = μ₂F_n1 – сила трения скольжения между доской и горизонтальной плоскостью; F_n1 – сила нормального давления доски с брусом на горизонтальную плоскость.

F_n1 = (m₁+m₂)g. (4)

Из выражений (3) и (4) получим:

F₀ = m₁μ₁g + m₂μ₁g +μ₂(m₁ + m₂)g = (m₁ + m₂) (μ₁ +μ₂)g = 22 Н.

Ответ: W_m = 2,5 м/с²; F₀ = 22 Н.