Лекция 16. Атом водорода

Для атома водорода 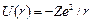, где r –расстояние между ядром и электроном. В сферической системе координат уравнение Шредингера:

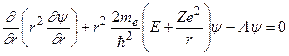, (3.3)

где 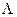– оператор Лежандра. Ядро считается неподвижным. Чтобы учесть его движение, нужно заменить массу электрона на приведенную массу.

Уравнение (3.3) решается по методу разделения переменных:

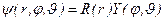. (3.3а)

Из (3.3) следует:

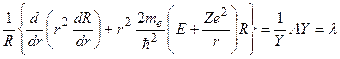, (3.4)

где 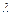– постоянная разделения. Приходим к независимым уравнениям для угловой части Y и радиальной части R волновой функции:

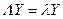, (3.5)

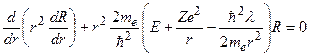. (3.6)

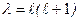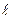Постоянная разделения , где – орбитальное квантовое число. В уравнении (3.6) сумма электростатической и центробежной энергий играет роль эффективной потенциальной энергии (рис.3.1): 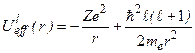. (3.7)

Потенциальная энергия имеет «яму» с минимальным значением на расстоянии

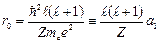, (3.7a)

где 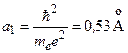– радиус первой боровской орбиты. Глубина «ямы»:

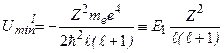,(3.7б) 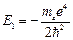энергия основного состояния водорода.

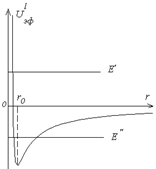Если энергия частицы положительна ( 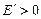), то ее движение инфинитно. Если энергия отрицательна ( 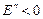), то частица находится в потенциальной яме (финитно). Рассмотрим далее решение уравнения (3.6) при отрицательных значениях энергии. Введем безразмерные переменные:

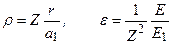. (3.8)

Решение ищется в виде:

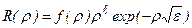, (3.9)

Рис.3.1 Функция 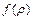удовлетворяет уравнению:

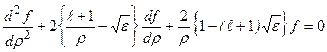. (3.10)

Решение ищется в виде бесконечного ряда

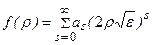. (3.11)

Можно получить рекуррентное соотношение

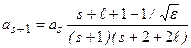. (3.11а)

Ряд (3.11) с коэффициентами (3.11а) расходится быстрее, чем 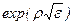. Естественное условие будет удовлетворяться, если функцию 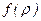рассматривать в виде полинома некоторой степени 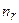. Ряд (3.11) становится полиномом степени 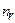при условии :

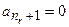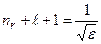. (3.12)

Это условие определяет собственные значения энергии водородоподобного атома:

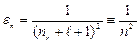. (3.12а)

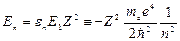. (3.13)

Это – в точности формула Бора.

Число 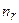- радиальное квантовое число, главное квантовое число:

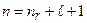. (3.13a)

При фиксированном числе n орбитальное квантовое число принимает n значений от 0 до n – 1:

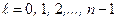. (3.14)

Радиальная волновая функция (3.9) зависит от квантовых чисел 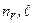. Удобнее пользоваться набором n, 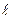. Стационарные состояния водородоподобного атома описываются волновыми функциями (3.3а):

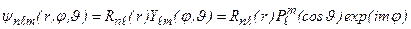. (3.15)

Функция 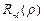выражается через обобщенные полиномы Лягерра:

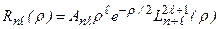. (3.15а)

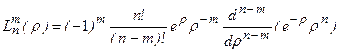. При m=0 полиномы 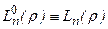- полиномы Лягерра.

Состояние водородоподобного атома характеризуется набором чисел 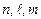. Значение энергии каждого состояния (3.13) определяется только главным квантовым числом. Ситуация, при которой различным волновым функциям отвечает одно и то же значение энергии, характерна для вырожденных состояний. Для водородоподобного атома каждое значение энергии вырождено по магнитному квантовому числу и по орбитальному квантовому числу. Кратность вырождения уровней - это количество различных волновых функций, отвечающих одному и тому же значению энергии. Для водородоподобного атома кратность вырождения определяется суммой:

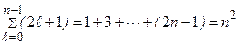. (3.16)

Каждый уровень энергии водородоподобного атома является 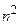– кратно вырожденным.

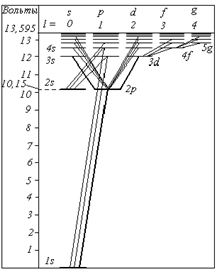
Состояния электрона в атоме обозначают с помощью буквы, которая соответствует численному значению орбитального квантового числа, а также с помощью цифры, стоящей перед этой буквой и соответствующей значению главного квантового числа: 1s; 2s, 2p; 3s, 3p, 3d; 4s, 4p, 4d, 4f;... Диаграмма уровней энергии атома водорода - диаграмма Гротриана .

Состояние 1s –основное состояние. Остальные состояния возбужденные. Некоторые волновые функции для водородоподобного атома:

n = 1 – состояние 1s:

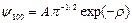(3.17)

n = 2 – состояние 2s:

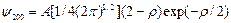
состояние 2p:

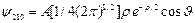
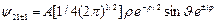(3.17а)

Постоянная .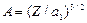

Переходы между различными состояниями возможны при выполнении правил отбора: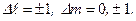

Квадрат модуля волновой функции (3.15) - плотность вероятности того, что электрон находится в элементе объема 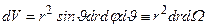, где 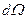– элемент телесного угла:

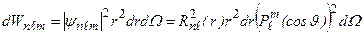. (3.18)

Распределения по углам и по радиусу - независимы. Вероятность углового распределения совпадает с вероятностью состояний ротатора. Распределение электронного заряда по радиусу:

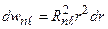. (3.19)

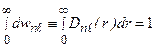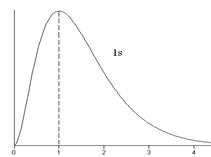
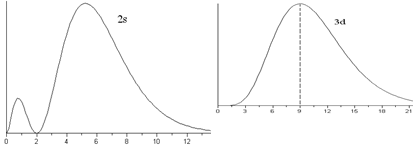
Условие нормировки . Величина 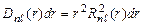- вероятность того, что электрон находится на расстоянии от r до r + dr от ядра атома. Графики функции 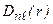для некоторых состояний изображены на рис.3.3.

Функция 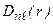в состояниях с максимальным значением орбитального квантового числа 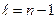. Число 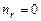. Из (3.11): 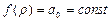. Так что 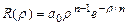. Плотность вероятностей в этих состояниях: 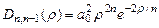. Это «одногорбая» функция, имеет максимум при 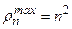, т.е. на расстояниях 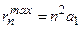– радиусов боровских орбит. В состояниях 1s, 2p, 3d, 4f ,... наиболее вероятно найти электрон на расстояниях, равных боровским радиусам. . С возрастанием числа n ширина кривой 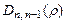вблизи 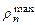становится более узкой, при 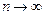функция 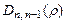стремится к дельта–функции 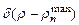. В этом проявляется принцип соответствия. Для получения полной картины распределения электронной плотности в

пространстве необходимо учесть угловую зависимость по формуле (3.18).

Волновые функции (3.17)–(3.17в) описывают состояния с центрально–симметричным распределением заряда вокруг ядра, так что в этих состояниях электрический дипольный момент отсутствует. Из-за вырождения уровней энергии в атоме водорода существуют состояния с несимметричным распределением электронного заряда относительно плоскости z = 0. Например, суперпозиция волновых функци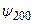й и 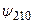, отвечающих уровню энергии с n = 2:

.

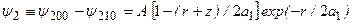Эта волновая функция имеет узловую поверхность 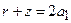- параболоид вращения с осью z и фокус в начале координат. Распределение электронной плотности несимметрично относительно плоскости 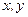: среднее положение электрона вдоль оси z отлично от нуля: 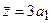. В этом состоянии атом водорода обладает электрическим дипольным моментом.