Проверка основного уравнения динамики вращательного движения

Лабораторная работа №5.

1. Теоретическое введение.

Основное уравнение динамики вращательного движения тела устанавливает связь между вращающим моментом М, действующим на тело, моментом инерции J и его угловым ускорением e.

Записывается оно так:

M=J× e (1) Если момент инерции тела постоянен, то разные вращающие моменты М₁ и М₂ сообщат телу разные угловые ускорения e₁ и e₂, т.е. будем иметь:

M₁=J×e₁;

M₂=J×e₂

Сравнивая эти выражения, получаем:

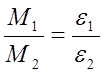(2)

С другой стороны, один и тот же вращающий момент сообщит телам с разными моментами инерции различные угловые ускорения.

Действительно, M=J₁×e₁;

M=J₂×e₂,

т.е. J₁×e₁=J₂×e₂,

или 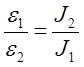(3)

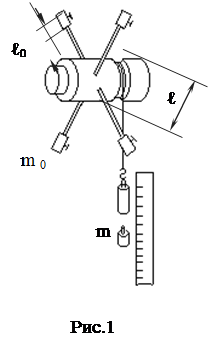Для проверки основного уравнения вращательного движения (1), или, что-то же самое, соотношений (2) и (3) может быть использован маятник Обербека, который представляет собой маховик крестообразной формы (рис.1). Вдоль стержней маховика могут перемещаться грузы m₀. На оси маховика находится валик, на который наматывается нить с привязанным к ней грузом m. Когда груз, привязанный к нити, падает, нить разматывается и приводит маховик в равноускоренное вращательное движение.

Сила, вызывающая вращение вала – есть сила натяжения нити. Ее можно определить из следующих соображений. По второму закону Ньютона произведение массы движущегося тела на его ускорение равно сумме сил, действующих на тело

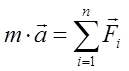
На падающее равноускоренно тело массой m действуют две силы – вес тела P=m×g, направленный вниз, и сила натяжения нити, направленная вверх.

Поэтому m×a=m×g – F_н

откуда F_н=m×g – m×a (4)

Следовательно, вращающий момент будет равен:

M=F_н×r=(m×g – m×a)×r, (5)

где r – радиус валика.

Цель работы: проверка соотношений (3) и (4), а следовательно, и основного уравнения вращательного движения (1), из которого были получены эти соотношения.

2. Приборы и принадлежности.

1) Маятник Обербека.

2) Набор грузов.

3) Секундомер.

4) Штангенциркуль.

5) Миллиметровая линейка.

3. Порядок выполнения работы.

Задача 1. Проверка зависимости углового ускорения от величины вращающего момента при неизменном моменте инерции (соотношение (2)).

1. Снять подвижные грузы m₀ с маховика.

2. Измерить штангенциркулем диаметр валика в трех разных направлениях и найти его радиус.

3. Подвесить к концу шнура груз m. Груз начнет опускаться с ускорением a, а маховик – вращаться с угловым ускорением e.

4. Одновременно с началом опускания груза пустить в ход секундомер и отметить по масштабной линейке высоту падения груза h, а по секундомеру – время ее движения t (время падения груза с одной высоты h определяют три раза и берут среднее значение).

5. По формуле 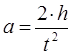определить линейное ускорение груза. С таким же ускорением движутся точки на поверхности валика.

6. Зная радиус валика, найти угловое ускорение валика .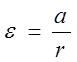

7. Найти вращающий момент по формуле (5) M=F_н∙r, где F_н – сила натяжения нити, равная как указано выше m∙g - m∙a.

8. Повторить опыт, изменив массу падающего груза (т.е. изменив вращающий момент).

9. Проверить правильность соотношения (2).

10. Вычислить момент инерции маховика J₀ без грузов на стержнях по формуле J₀ = 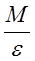и взять среднее значение из двух результатов, т.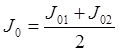е. , где ; .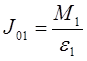

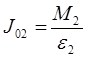Данные измерений и вычислений занести в таблицу 1.

Таблица 1

№ опыта

№ измер.

m, кг

h, м

t, c

r, м

a, м/с2

e, 1/с2

Fн, Н

M, Н∙м

J0, кг∙м2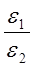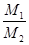

I

tср

II

tср

J0ср

Задача 2. Проверка зависимости углового ускорения от величины момента инерции при неизменном вращающем моменте (соотношение (3)).

1. Определить массу подвижного груза m₀ (масса указана на приборе).

2. Закрепить подвижные грузы на стержнях и привести валик во вращение, измеряя, как и в прежнем опыте, высоту и время падения груза m.

3. Определить расстояние R от оси до центров масс грузов m₀. Оно определяется по формуле: ,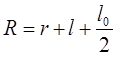

где r – радиус валика,

l – расстояние от груза m₀ до валика,

l₀ – длина груза m₀ (определяется штангенциркулем).

4. Оставляя массу падающего груза неизменной, передвинуть грузы m₀ на расстояние R₂>R₁, и приведя маховик во вращение, снова определить h и t. Можно изменить момент инерции маховика, сняв с него два (противоположно расположенных) груза m₀.

5. Посчитать момент инерции маховика с грузами как сумму момента инерции маховика без грузов (берется среднее значение J₀ из опыта I) и момента инерции грузов J′, которые принимают за материальные точки, т.е.

J=J₀+J′,

где J′=2∙m₀∙R² или J′=4∙m₀∙R², в зависимости от того, два или четыре груза с массой m₀ надеты на стержни.

6. Посчитать линейное и угловое ускорения.

7. Проверить правильность соотношений (3).

Данные измерений и вычислений занести в таблицу 2.

Таблица 2

№ измер

№ опыта

m, кг

h, м

t, с

r, м

m0, кг

l, м

l0, м

R, м

a, м/с2

e, 1/с2

J0, кг∙м2

J′, кг∙м2

J, кг∙м2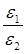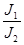

I

tср

II

tср

8. Подсчитать относительную и абсолютную погрешности углового ускорения, используя формулу 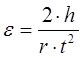(как для косвенных измерений).

4. Вопросы, предлагаемые для защиты работы:

1. Что называется моментом инерции материальной точки?

2. Что называется моментом инерции тела? Каков его физический смысл? В каких единицах измеряется момент инерции?

3. Что называется вращающим моментом? В каких единицах он измеряется?

4. Угловое ускорение, его связь с линейным ускорением.

5. Записать основное уравнение вращающего движения.

6. Какое соотношение связывает угловое ускорение вращающегося тела с вращающим моментом, действующим на тело при неизменном моменте инерции? Объяснить, как проверялось его соотношение в данной работе.

7. Как связано угловое ускорение вращающегося тела с его моментом инерции при постоянном вращающем моменте?

8. Как определить момент инерции маятника Обербека?

9. При любом ли расположении масс на крестовине их можно считать точечными?

10. Вывести формулу (5) для маятника Обербека.

11. Вывести формулу относительной погрешности углового ускорения 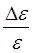и абсолютной погрешности .

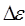Литература.

1. Введение к работам №№3,4,5.

2. Г.А.Зисман и О.М.Тодес «Курс общей физики» т.1, гл.III, §II

3. А.А.Летлаф и др. «Курс физики» т.I, гл.IV,§ I.

4. И.В.Савельев «Курс общей физики» т.I, гл.V, §§34-40.

5. Т.И.Трофимова «Курс физики», М: Высшая школа, 1985г.