Конвекция и массоотдача

Под конвективным массопереносом понимают процесс переноса вещества при движении жидкости иди газа. Этот процесс происхо­дит как бы механически -макрообъемными частицами жидкостного или газового потока.

Рассмотрим некоторые вопросы переноса массы внутри одной фазы, т.е. от ядра потока к границе раздела фаз или наоборот -от границы раздела фаз в ядро потока. Полагаем, что в нашем случае процесс массопереноса происходит между газом и жид­костью (процесс абсорбции, т.е. массоперенос идет из фазы Ф_у в фазу Ф_х), режим движения турбулентный.

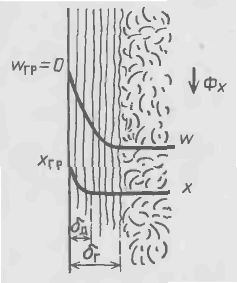
Гидродинамические особенности турбулентного потока в канале были рассмотрены в гл. 3. Здесь же следует отметить влияние гидродинамических условий на перенос вещества. В пограничном слое толщиной δ_r (рис. 15-2) происходит резкое, близкое к линей­ному изменение концентраций; поскольку в этой области потока скорость процесса определяется молекулярной диффузией, роль конвективной диффузии мала. Это объясняется тем, что на границе раздела фаз усиливается тормозящее действие сил трения между фазами и сил поверхностного натяжения на границе жидкой фазы. Образование гидродинамического пограничного слоя вблизи по­верхности раздела фаз ведет к возникновению в нем диффузионного пограничного слоя толщиной δ_Д, обычно не совпадающей с δ_r. В ядре потока массоперенос осуществляется в основном турбу­лентными пульсациями, поэтому концентрация распределяемого вещества в ядре потока практически постоянна. Как отмечалось выше, перенос вещества движущимися частицами, участвующими в турбулентных пульсациях, называют турбулентной диффузией. Перенос вещества турбулентной диффузией описывается уравне­нием, аналогичным уравнению (15.14а):

М = -(D + Ul)Fдc/дn = -(D + ɛ_д)Fдc/дn, (15.17)

где U -средняя пульсационная скорость движения частицы жилкости в поперечном направлении; l-расстояние, на которое перемещаются частицы в поперечном на­правлении; ɛ_д = Ul -коэффициент турбулентной диффузии.

Рис. 15-2. Профили изменения скорости потока жид­кой фазы (w) и концентрации растворенного вещест­ва (х) в турбулентном потоке

Очевидно, что пограничный слой со­здает основное сопротивление процессу переноса.

Перенос по рассмотренной схеме на­зывают массоотдачей. По мере прибли­жения к ламинарному режиму погранич­ный слой сильно разрастается, как бы заполняя все сечение потока. В этих условиях конвективный перенос идет в направлении, параллельном движению потока. При этом перенос массы к границе раздела определяется в основном молекулярной диффузией. Очевидно, что скорость конвективного переноса существенно выше скорости мо­лекулярной диффузии. Поэтому развитие турбулентности способст­вует ускорению конвективного переноса массы.

Теоретическим путем толщину пограничного диффузионного слоя можно определить для самых простых случаев массопереноса. Поэтому использование первого закона Фика

М= -DFτдc/дn

для описания процесса затруднительно, так как закон распреде­ления концентраций в пограничном слое (дс/дп) неизвестен.

Maccooтдачу, так же как и конвекцию, подразделяют на естест­венную и вынужденную, или принудительную. При естественной массоотдаче движение жидкости происходит вследствие разности плотностей в разных точках жидкости, а при вынужденной -вслед­ствие затраты энергии на движение потока извне с помощью насоса, мешалки и т.п. Очевидно, что естественная массоотдача процесс медленный и в технике встречается редко, но часто является сопутствующим процессом вынужденной массоотдачи.

По аналогии с эмпирическим законом охлаждения Ньютона (или уравнением теплоотдачи) уравнение массоотдачи имеет сле­дующий вид:

d²M=b_x(x_гр-x)dFdτ, (I5.18)

где b_x -коэффициент пропорциональности коэффициент массоотдачи.

При установившемся процессе для всей поверхности F массо­отдачи при τ = 1 с уравнение (15.18) принимает вид

М =b_yF(y - y_гр) (15.18a)

Для фазы Ф уравнение массоотдачи будет аналогично урав­нению (15.18а), но с соответствующей заменой концентраций:

М =b_xF(x_гр - x) (15.19)

Из уравнений (15.18) и (15.19) найдем размерность коэффи­циентов массоотдачи:

.

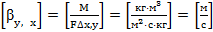Коэффициент массоотдачи показывает, какое количество ве­щества переходит от единицы поверхности раздела фаз в ядро потока (или наоборот) в единицу времени при движущей силе, равной единице.

Коэффициент массоотдачи, в отличие от коэффициента массопередачи, характеризует скорость переноса вещества внутри фазы конвекцией и молекулярной диффузией одновременно. Коэффи­циент массоотдачи зависит от многих факторов (физических свойств фазы, скорости потока, определяющих геометрических размеров и т.д.) и является аналогом коэффициента теплоотдачи. Ввиду сложной зависимости коэффициента массоотдачи от этих факторов получение обобщенной зависимости для определения величины b_y или b_x крайне затруднительно.

При разработке моделей массопереноса обычно принимают допущение о том, что на поверхности раздела фазы находятся в со­стоянии равновесия, а общее сопротивление процессу переноса складывается из суммы сопротивлений двух фаз. Из этих допуще­ний следует, что на границе раздела фаз отсутствует сопротивление процессу (т. с. равновесие на границе устанавливается очень быстро -во всяком случае, быстрее изменения средней концентрации в ядре фазы, что для ряда процессов массопереноса доказано эксперимен­тально) и что процесс массопереноса подчиняется правилу адди­тивности фазовых сопротивлений.

Вследствие взаимного влияния движения фаз, участвующих в процессе массопереноса, математическое описание скорости про­цесса чрезвычайно сложно. Поэтому решение дифференциальных уравнений переноса (см. гл. 3) оказывается возможным лишь в простейших случаях, когда точно известна поверхность контакта фаз и, как правило, при их ламинарном движении. В этом случае скорость процесса определяют совместным решением уравнений переноса в каждой из фаз.

Пленочная (двухпленочная) модель Льюиса и Уит­мена основана на предпосылках, ранее рассмотренных Нернстом при изучении им растворения твердых тел в жидкостях. По этой модели с обеих сторон поверхности контакта фаз образуются неподвижные или ламинарно движущиеся пленки, в которых пере­нос вещества осуществляется только молекулярной диффузией. Эти пленки отделяют поверхность контакта фаз от ядра потока, в ко­тором концентрация практически постоянна; все изменения кон­центрации вещества происходят в пленке.

В соответствии с пленочной моделью интегрирование уравнении (15.14а) приводит к выражению

М = (D/δ_пл)F(c_о-c_гp), (15.20)

где δ_пл -толщина пленки; с₀ и с_гр -средняя концентрация в ядре фазы и концентрация на границе раздела фаз соответственно.

Сравнивая последнее уравнение с уравнениями (15.18) и (15.19), получим

b = D/ δ_пл (15.21)

Из уравнения (15.21) следует, что величина Р обратно пропор­циональна толщине пленки, которая определяется гидродинами­ческими условиями: чем более турбулентны фазы, тем меньше δ_пл и, следовательно, тем выше b.

Уравнение (15.21) также показывает, что по пленочной модели коэффициент массоотдачи линейно зависит от коэффициента диффузии, что часто не подтверждается экспериментально. Кроме того, эта теория не учитывает деформации поверхности контакта фаз и переноса вещества турбулентными пульсациями.

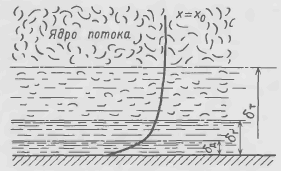
Рис. 15-3. К пояснению медали пограничного диффузионного слоя.

В модели пограничного диффузионного слоя, которую можно считать дальнейшим развитием пленочной модели, отра­жено влияние гидродинамических условий на процесс массопереноса. По этой модели (рис. 15-3) кончен фация вещества, постоян­ная в ядре потока, в турбулентном подслое толщиной δ_г, постепенно снижается при приближении к тираничному слою (т.е. в буферном подслое), в котором соизмеримы молекулярные и турбулентные силы вязкости, т.е. v ≈ v_т. С уменьшением масштаба пульсаций в вязком подслое толщиной 6, концентрация снижается сущест­венно быстрее. В глубине вязкого подслоя, внутри тонкого диффу­зионного подслоя толщиной δ_д молекулярный перенос становится основным, при этом v » v_т. Толщина пограничного диффузионного слоя δ_д меньше толщины вязкого пограничного слоя δ_г , причем

δ_д = δ_г (D/v)^1/m , (15.22)

где m - показатель степени, отражающий закон затухания турбулентного переноса вблизи границы раздела фаз.

Для систем жидкость -твердое тело m = 3, а для систем газ(пар) -жидкость и жидкость-жидкость m = 2. Поэтому [из уравнений (15.20) и (15.22)] для систем твердое тело-жидкость М ~ D^0,66 , а для систем газ(нар)-жидкость и жидкость-жидкость М ~ D^0,5.

Модель обновления поверхности фазового контакта часто называют моделью проницания, или пенетрационной. По этой модели предполагается, что турбулентные пульсации по­стоянно подводят к поверхности раздела фаз свежую жидкость и смывают порции жидкости, уже прореагировавшей с газом (паром), т.е. каждый элемент поверхности жидкости взаимодействует с газом (паром) в течение некоторого времени τ (время контакта или обновления), после чего данный элемент обновляется. На основе этой модели, принимая время т контакта постоянным для всех элементов поверхности, Хигби получил уравнение для определения коэффициента массоотдачи: