ТОК В МЕТАЛЛАХ, Основные ЖИДКОСТЯХ И ГАЗАХ ФОРМУЛЫ 5 страница

I = 0,8 А, Iк.з. = 2 А

h = ?

Iк.з = e. (1)

По закону Ома для полной цепи:

I= Re r . (2)

Используя закон Джоуля–Ленца, найдем количество тепла, выделившегося за время t на сопротивле-нии R

Q = I 2Rt = × R ×t,

R r а во всей цепи

Q = I 2 (R + r)×t = I ×e×t = R+ r. Коэффициент полезного действия:

h = Q= R+r, или с учетом (1) и (2)

h = I= 0,4 = 40%. к.з

ЗАДАЧА 18. Определить какой ток создает электрон, вращающийся вокруг ядра в атоме водорода, ес-ли радиус его орбиты принять равным 5,3×10−9см.

Дано:

r = 5,3×10−11 м е =1,6×10−19 Кл m = 9,1×10−31 кг

I = ?

Решение

Сила тока:

I = t= etN= e×n = e×v ,

где N – число оборотов электрона за время t; n – частота.

При движении электрона по круговой орбите роль центростремительной силы играет кулоновская сила взаимодействия электрона с ядром:

mv2 e2

r 4pe0r2откуда

v =

следовательно

e

4pe0rm

I = 2p×r4pe0rm=1,05×10−3 A.

ЗАДАЧА 19. N – одинаковых аккумуляторов соединены последовательно, причем k из них включены навстречу другим. ЭДС каждого элемента равна 1, внутреннее сопротивление – r1. Какой ток установится в цепи, если батарею замкнуть на сопротивление R?

e

e

e

e

.

=

I

.

Q

=

R

R

R

R

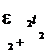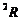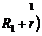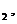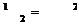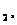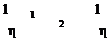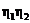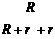Дано: e , k,

R, N, r1

I = ?

Решение

Запишем закон Ома для полной цепи

I = R+r.

Так как элементы соединены последовательно, то r = Nr1. ЭДС батареи равна алгебраической сумме ЭДС элементов:

e=(N −k)× 1−k× 1= 1×(N −2k)

Следовательно, ток в цепи

e (N −2k) R + N ×r

ЗАДАЧА 20. При поочередном замыкании аккумулятора на резисторы R1 и R2 в последних выделились равные количества теплоты. Найти внутреннее сопротивление аккумулятора.

Дано: Решение

R1, R2 СогласнозаконуДжоуля–Ленца:

r=? Q=I1R×t=(e2Rt2, 2 = I2 2 ×t= (R 2Rr) .

ТаккакQ1 =Q2,то e2R t e2R t ( 1+ r) (R2+ r)

R R

( 1 + r) (R2 + r)

откуда r = R R2 .

ЗАДАЧА 21. Первый аккумулятор имеет КПД h1, второй, замкнутый на такое же сопротивление, – h2. Каким будет КПД, если замкнуть на это сопротивление оба аккумулятора, соединенные последовательно?

Решение

КПД аккумуляторов:

h = R+r, h2= R+r,

где R – внешнее сопротивление; r1, r2 – внутренние сопротивления первого и второго аккумуляторов соот-ветственно, получаем

r=R( −h ),r=R( −h2),1 2

тогда h= 1 2=h +h2−h h2.

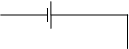
ЗАДАЧА 22. В схеме e = 2,1 В, e2= 1,9 В, R1 = 45 Ом, R2 = 10 Ом и R3 = 10 Ом. Найти силу тока во всех участках цепи. Внутренним сопротивлением элементов пренебречь.

R

e

R

R

R

R

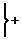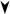
Дано:

e = 2,1 В

e2= 1,9 В

Решение

e1

R1 = 45 Ом R2 = 10 Ом

R3 = 10 Ом

e2 обход

1 R3

I1 = ?

I2 = ?

обход I1 I3

I3 =? R2 I2

По первому закону Кирхгофа:

I2 + I3 = I1.

Запишем уравнения для замкнутых контуров по второму закону Кирхгофа: I11+ I33= 1,

I11+ I22=e2, или

45I1+10I3= 2,1, 4,5I1+ I3= 0,21, 45I1+10I2=1,9, 4,5I1+ I2= 0,19,

4,5I1 + I1 – I2 = 0,21.

5,5I1− I2= 0,21, ü4,5I1+ I2= 0,19, þ

10 I1 = 0,4.

I1 = 0,04 A, I2 = 0,19 – 4,5 · 0,04 = 0,01 A, I3 = 0,03 A.

КОНТРОЛЬНАЯ РАБОТА 3

Студент заочник должен решить семь задач того варианта, номер которого совпадает с цифрой спра-ва его шифра.

Пример. Номер зачетной книжки 13701. Студент решает седьмой вариант.

Вариант Номера задач

0 3 16 23 39 43 55 62 1 6 20 26 37 50 58 70 2 5 13 28 40 46 52 64 3 10 18 24 31 48 56 61 4 7 14 21 35 44 59 68 5 2 11 29 34 49 54 67 6 8 17 25 32 41 60 65 7 9 12 27 36 47 53 69 8 1 15 22 38 42 57 63 9 4 19 30 33 45 51 66

1. На двух одинаковых каплях масла радиусами r =8,22×10−5м находятся одноименные равные по ве-личине заряды. Определить величину этих зарядов, если сила кулоновского отталкивания уравновешивает силу гравитационного притяжения капель. Плотность масла r = 0,9×103кг/м3.

2. В центре квадрата, в вершинах которого находятся одинаковые заряды q, помещен отрицательный заряд Q. Какова должна быть величина этого заряда, чтобы система находилась в равновесии?

3. Два шарика, одинаковые по радиусу и весу, подвешенные на нитях одинаковой длины, опускаются в жидкий диэлектрик, плотность которого r1 и диэлектрическая проницаемость – e1. Какова должна быть плотность материала шариков, чтобы углы их расхождения в воздухе и диэлектрике были одинаковы?

4. Два одинаковых заряженных шарика, находящихся на расстоянии 0,2 м, притягиваются с силой 1= 4×10−3H. После того как шарики были приведены в соприкосновение и затем разведены на прежнее

расстояние, они стали отталкиваться с силой 2= 2,25×10−3H. Определить первоначальные заряды шаров?

5. На двух одинаковых капельках воды находится по одному лишнему электрону, причем сила элек-трического отталкивания капелек уравновешивает силу их взаимного тяготения. Каковы радиусы капелек?

6. Заряды +Q, –Q и +q расположены в углах правильного треугольника со стороной а. Каково на-правление силы, действующей на заряд +q?

7. Три маленьких шарика массой m = 10 г каждый подвешены на шелковых нитях длиной по 1 м, сходящихся наверху в одном узле. Шарики одинаково заряжены и висят в вершинах равностороннего тре-угольника со стороной 0,1 м. Каков заряд каждого шарика?

8. Тонкий длинный стержень равномерно заряжен с линейной плотностью t =10нКл/м. На расстоя-нии а = 10 см от нити, против ее середины находится точечный заряд Q = 1 нКл. Вычислить силу F, действующую на этот заряд со стороны заряженной нити.

9. Тонкая бесконечная нить согнута под углом 90º. Нить несет заряд, равномерно распределенный с линейной плотностью t =1мКл/м. Определить силу F, действующую на точечный заряд Q = 0,1 мкКл, расположенный на продолжении одной из сторон и удаленный от вершины угла на а = 50 см.

10. Три одинаковых заряда Q = 1 нКл каждый расположены по вершинам равностороннего треуголь-ника. Какой отрицательный заряд Q1 нужно поместить в центре треугольника, чтобы его притяжение урав-новесило силы взаимного отталкивания зарядов? Будет ли это равновесие устойчивым?

11. Электрическое поле создано двумя точечными зарядами q1 = 10 нКл и q2= −20нКл, находящи-мися на расстоянии d = 20 см друг от друга. Определить напряженность Е поля, в точке удаленной от пер-вого заряда на r1 = 30 см и от второго на r2 = 50 см.

12. Три одинаковых заряда q =10−9Кл каждый, расположены в вершинах прямоугольного треуголь-

26

F

F

ника с катетами а = 40 см и b = 30 см. Найти напряженность электрического поля, создаваемого всеми за-рядами в точке пересечения гипотенузы с перпендикуляром, опущенным на неё из вершины прямого угла.