Теплопроводность. Закон Фурье. Коэффициент теплопроводности

Теплопроводность возникает при наличии разности температур, вызванной какими-либо внешними причинами. При этом молекулы газа в разных местах имеют разные средние кинетические энергии (скорости хаотического теплового движения молекул), что приводит к направленному переносу молекулами газа внутренней энергии.

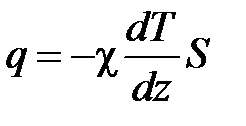Опытным путем установлено, что в случае, если в какой-либо среде вдоль некоторого направления z температура не остается постоянной, то вдоль этого направления устанавливается поток тепла, величина которого определяется формулой.

Закон Фурье:

где q – количество теплоты, протекающее за единицу времени через площадку S, расположенную перпендикулярно к оси z, c – коэффициент теплопроводности;

Градиент температуры:

Знак «минус» в законе Фурье отражает то обстоятельство, что направление, в котором возрастает температура, и направление, в котором течет тепло, противоположны, т.е. что тепло течет в направлении убывания температуры. Поток тепла в уравнении Фурье – величина алгебраическая: если тепло течет в положительном направлении оси z, q положительно, если же тепло течет в отрицательном направлении оси z, то q отрицательно.

Чтобы вычислить количество теплоты Q, протекающее через площадку S за время t, нужно q умножить на t:

Вычислим поток тепла в газе, основываясь на молекулярно-кинетических представлениях.

Если температура газа в разных местах различна, то и средняя энергия молекул также будет различной. Перемещаясь вследствие теплового движения из одних мест в другие, молекулы переносят запасенную ими энергию, что обуславливает процесс теплопроводности.

Кроме факторов, определяющих скорость диффузии, т.е. средней скорости молекул , <υ> и длины свободного пробега λ, количество переносимой молекулами энергии должно зависеть от способности молекул запасать энергию, т.е. От теплоемкости газа. Поскольку поток молекул определяется их числом в единице объема, то и теплоемкость должна относиться к единице объема.

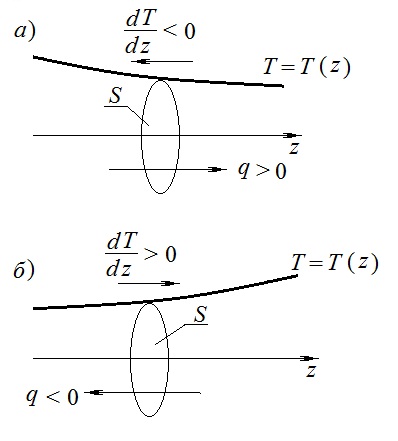
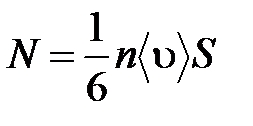Пусть в газе поддерживается градиент температуры вдоль направления z. Представим мысленно поверхность S, перпендикулярно к этому направлению. Количество молекул, пролетающих в единицу времени через поверхность S в каждом направлений (слева направо и справа на лево), будем считать равным:

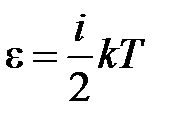Вычислим тепловой поток.

Каждая молекула имеет энергию , соответствующую температуре в том месте, где

произошло ее столкновение с другой молекулой. В среднем это столкновение происходит на расстоянии от S, равном длине свободного пробега λ. Поэтому молекулам, летящим слева на право, надо приписывать среднюю энергию <ε₁>, соответствующую температуре Т₁=Т(z–λ), т.е. температуре в плоскости z–λ, молекулам же, летящим справа налево – среднюю энергию <ε₂>, соответствующей температуре Т₂=Т(z+λ).

Величины n и <υ> зависят от температуры. Число частиц, летящих через площадку S во встречных направлениях, не могут быть различными. Если бы они оказались неодинаковыми, то кроме потока тепла через площадку S наблюдался бы поток вещества (диффузия) – происходило бы перемещение газа из одной части пространства в другую. В самом начале сделали предположение, что движение газа, как целого, отсутствует.

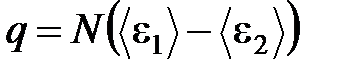Таким образом, для теплового потока q через поверхность S получается выражение:

где N определяется формулой .

Подстановка значений N, <ε₁> и <ε₂> приводит к формуле:

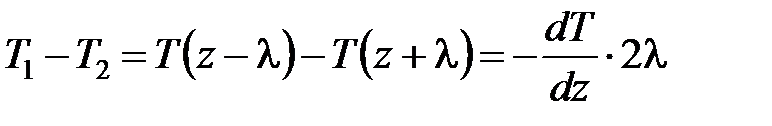Вследствие малости λ разность Т₁–Т₂ можно представить в виде:

где - производная Т по z в том месте, где расположена поверхность S. Подстановка выражения для разности температур приводит к формуле Фурье:

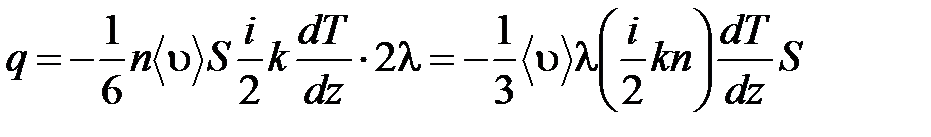
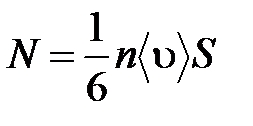
Полученная формула совпадает с эмпирическим уравнением Фурье, если положить теплоемкость равной:

Величина молярная теплоемкость газа при постоянном объеме.

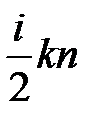
Следовательно выражение представляет собой теплоемкость при постоянном.

объеме количества газа, содержащего n молекул, т.е. теплоемкость единицы объема газа. Эту теплоемкость можно получить, умножив удельную теплоемкость газа с_V при постоянном объеме на плотность газа ρ. Следовательно

Учитывая это значение, получим для теплопроводности газа следующее выражение:

31. Первое начало термодинамики (ПНТ).