Законы Стефана-Больцмана и смещения Вина

Лекции 1,2

КВАНТОВЫЕ СВОЙСТВА ИЗЛУЧЕНИЯ

Тепловое излучение

Свечение тел, обусловленное нагреванием, называется тепловым излучением. Тепловое излучение совершается за счет энергии теплового движения атомов и молекул вещества (т.е., за счет внутренней энергии) и свойственно всем телам при температурах выше абсолютного нуля Кельвина. При высоких температурах излучаются короткие (видимые и ультрафиолетовые) электромагнитные волны, при низких – преимущественно длинные (инфракрасные).

Тепловое излучение – практически единственный вид излучения, который может быть равновесным. Предположим, что нагретое (излучающее) тело помещено в полость, ограниченную идеально отражающей оболочкой. С течением времени, в результате непрерывного обмена энергией наступит равновесие. Допустим, что равновесие нарушилось и тело излучает энергии больше, чем поглощает. Тогда температура тела должна понижаться. В результате будет уменьшаться количество излучаемой телом энергии, пока не наступит равновесие. Все другие виды излучения являются неравновесными.

Количественной характеристикой теплового излучения служит излучательность тела – мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины, т.е.:

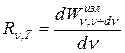
где 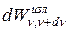- энергия электромагнитного излучения, испускаемого за единицу времени (мощность излучения) с единицы площади поверхности тела в интервале частот от ν до ν +dν. Единица измерения излучательности .

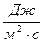Излучательность может быть представлена в виде функции длины волны:

,

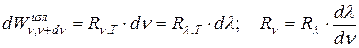так как 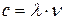, то

,

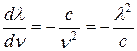где знак «минус» указывает на то, что с возрастанием одной из величин (частоты или длины волны) другая величина убывает. Поэтому в дальнейшем этот знак будем опускать. То есть:

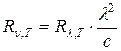. (1.1)

Можно также вычислить интегральную излучательность (ее называют просто излучательностью):

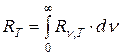(1.2)

Способность тел поглощать падающее на них излучение характеризуется поглощательной способностью:

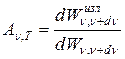
показывающей, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами от ν до ν +dν, поглощается телами. Поглощательная способность тела является безразмерной величиной. Величины 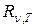и 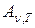зависят от природы тела, его термодинамической температуры и при этом различаются для излучений различных частот. Поэтому эти величины относятся к определенным температуре и частоте (вернее, узкому интервалу частот от ν до ν +dν) и называются спектральной плотностью излучательности 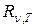и спектральной поглощательной способностью .

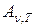Тело, способное поглощать полностью при любой температуре все падающее на него излучение называется абсолютно черным телом. Следовательно, для любых частот и температур для абсолютно черного тела справедливо:

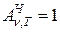
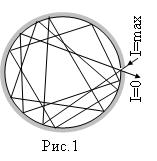Абсолютно черных тел в природе не существует. Идеальной моделью абсолютно черного тела является замкнутая полость с небольшим отверстием, внутренняя поверхность которой зачернена, рис.1. Луч света, попадающий внутрь такой полости, испытывает многократное отражение от стенок, в результате чего интенсивность вышедшего излучения оказывается практически равной нулю. Из-за подобного многократного отражения кажутся абсолютно черными окна домов.

Наряду с понятием абсолютно черного тела используется понятие серого тела – такого тела, поглощательная способность которого меньше единицы, но постоянна для всех частот и зависит только от температуры, материала и состояния поверхности тела. Таким образом, из определения серого тела следует, что:

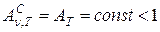
Аналогичным образом можно ввести понятие абсолютно белого тела (тела отражающего все падающее на него излучение):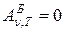

Закон Кирхгофа

Кирхгоф, исходя из второго закона термодинамики и анализируя условия равновесного излучения в изолированной системе тел, установил количественную связь между спектральной плотностью излучательности и спектральной поглощательной способностью тела, получившую название закона Кирхгофа: Отношение спектральной плотности излучательности к спектральной поглощательной способности не зависит от природы тела; оно является для всех тел универсальной функцией частоты (длины волны) и температуры:

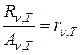(1.3)

для абсолютно черного тела 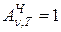, поэтому из закона Кирхгофа вытекает, что в этом случае: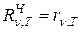

Таким образом, универсальная функция Кирхгофа 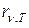представляет собой спектральную плотность излучательности абсолютно черного тела. Следовательно, для всех тел отношение 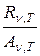равно спектральной плотности излучательности абсолютно черного тела.

Из закона Кирхгофа следует, что спектральная плотность излучательности любого тела всегда меньше универсальной функции Кирхгофа (при тех же значениях частоты и температуры), т.к. 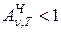. Кроме того, из (1.3) вытекает, что если тело не поглощает электромагнитной волны какой-то определенной частоты, то оно и не излучает электромагнитных волн такой длины волны, т.к. при 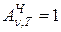и .

И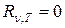спользуя закон Кирхгофа выражению для излучательности тела можно придать вид:

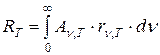
Для серого тела это выражение принимает вид:

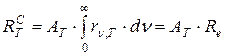(1.4)

где

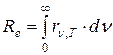(1.5)

излучательность абсолютно черного тела, которая зависит только от температуры.

Закон Кирхгофа описывает только тепловое излучение, являясь настолько характерным для него, что может служить надежным критерием для определения природы излучения. Излучение, которое не подчиняется закону Кирхгофа, не является равновесным (т.е. тепловым).

Законы Стефана-Больцмана и смещения Вина

Английские физики Стефан, анализируя экспериментальные данные в 1879 году, и Больцман, применяя термодинамический метод в 1884 году, решили задачу о зависимости универсальной функции Кирхгофа от частоты, однако лишь частично, установив зависимость излучательности 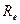от температуры. Согласно полученному ими закону Стефана-Больцмана, можно записать:

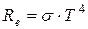(1.6)

то есть излучательность абсолютно черного тела пропорциональна четвертой степени его термодинамической температуры. 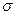-постоянная Стефана-Больцмана – ее экспериментальное значение .

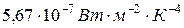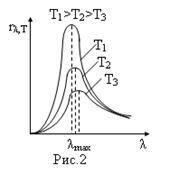
Закон Стефана-Больцмана, определяя зависимость 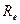от температуры, не дает ответа относительно спектрального состава излучения абсолютно черного тела. Из экспериментальных кривых зависимости универсальной функции Кирхгофа 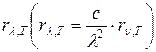от длины волны при различных температурах, рис.2, следует, что распределение энергии в спектре абсолютно черного тела является неравномерным. Все кривые имеют ярко выраженным максимум, который по мере повышения температуры смещается в сторону более коротких волн. Площадь, ограниченная кривой 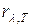и осью абсцисс, пропорциональна излучательности абсолютно черного тела 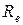и, следовательно, по закону Стефана-Больцмана, четвертой степени температур. Немецкий физик Вин, опираясь на законы термо- и электродинамики, установил зависимость длины волны 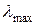, соответствующей максимуму функции Кирхгофа 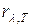, от температуры. Согласно закону смещения Вина:

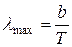, (1.7)

то есть длина волны, соответствующая максимальному значению спектральной плотности излучательности абсолютно черного тела, обратно пропорциональна его термодинамической температуре. 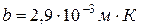- постоянная Вина. Выражение (1.7) называется законом смещения потому, что оно показывает смещение положения максимума 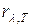по мере возрастания температуры в область коротких длин волн. Закон Вина объясняет, почему при понижении температуры нагретых тел в их спектре все сильнее преобладает длинноволновое излучение (например, переход белого каления в красное свечение при остывании расплавленного металла). Законы Стефана-Больцмана и Вина являются все - таки частными законами, так как не дают общей картины распределения энергии по частотам при различных температурах.

Формула Релея-Джинса

Следующая попытка теоретического вывода зависимости 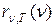принадлежит английским ученым Релею и Джинсу, которые применили при рассмотрении теплового излучения методы статистической физики, воспользовавшись классическим законом равномерного распределения энергии по степеням свободы.

Формула Релея-Джинса для спектральной плотности излучательности абсолютно черного тела имеет вид:

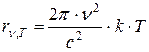, (1.8)

где 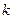- постоянная Больцмана.

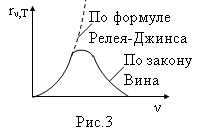Как показал эксперимент, выражение (1.8) согласуется с экспериментом только в области малых частот и больших температур. В области больших частот, рис.3, формула Релея-Джинса резко расходится с экспериментом. Кроме того, оказалось, что попытка получить закон Стефана-Больцмана из формулы Релея-Джинса приводит к абсурду. Действительно:

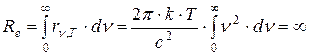
в то время как по закону Стефана-Больцмана 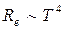. Этот результат получил название «ультрафиолетовой катастрофы» – в рамках классической физики не удалось объяснить законы распределения энергии в спектре абсолютно черного тела.

Формула Планка

Правильное, согласующееся с экспериментальными данными выражение для универсальной функции Кирхгофа (спектральной плотности излучательности абсолютно черного тела) было предложено Максом Планком (14.12.1900 г.). Согласно выдвинутой Планком квантовой гипотезе, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями – квантами, причем энергия кванта пропорциональна частоте колебаний:

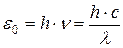(1.9)

где 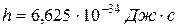- постоянная Планка. Так как излучение испускается порциями, то энергия 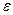осциллятора может принимать лишь определенные дискретные значения, кратные целому числу элементарных порций энергии :

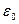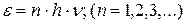
Используя статистические методы и представления о квантовом характере излучения, Планк получил для универсальной функции Кирхгофа следующее выражение:

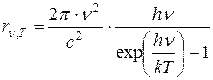, (1.10)

где .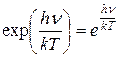

Полученная Планком формула блестяще согласуется с экспериментальными данными по распределению энергии в спектрах излучения абсолютно черного тела во всем интервале частот нуля до бесконечности и при различных температурах.

Из формулы Планка можно вывести частные законы, описывающие тепловое излучение.

В области малых частот, то есть при 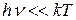(энергия кванта очень мала по сравнению с энергией теплового движения), из формулы Планка (10) можно получить формулу Релея-Джинса. Для доказательства этого разложим экспоненциальную функцию в ряд, ограничившись для рассматриваемого случая двумя первыми членами:

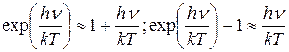
Подставляя последнее выражение в формулу Планка (14.10), находим, что:

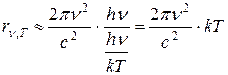
т.е. получили формулу Релея-Джинса (1.8).

В области больших частот, т.е. при 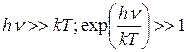(энергия фотона много больше энергии теплового движения) из формулы Планка (1.10) получается закон излучения Вина:

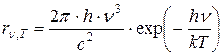
являющийся, таким образом, предельным случаем формулы Планка.

Из формулы Планка можно также получить закон Стефана-Больцмана. Согласно определению излучательности абсолютно черного тела:

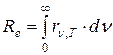
подставим значение универсальной функции Кирхгофа, полученное Планком:

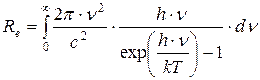(1.11)

Введем безразмерную переменную 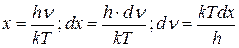, тогда формула (1.11) преобразуется к виду:

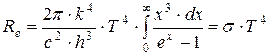(1.12)

где 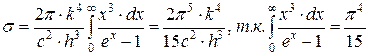, таким образом, формула Планка позволяет получить закон Стефана-Больцмана. Кроме того, подстановка числовых значения констант дает для постоянной Стефана-Больцмана величину, хорошо согласующуюся с экспериментальными данными.

Аналогичным образом можно получить при помощи формулы Планка закон смещения Вина.

Оптическая пирометрия

Совокупность методов измерения высоких температур, использующие зависимость спектральной плотности излучательности или интегральной излучательности тел от температуры называется оптической пирометрией. Приборы для измерения температуры нагретых тел по интенсивности их теплового излучения в оптическом диапазоне спектра называются пирометрами. В зависимости от того, какой закон теплового излучения используется при измерении температуры тел, различают: радиационную, цветовую и яркостную температуры.

Радиационная температура. Это такая температура абсолютно черного тела, при которой его излучательность равна излучательности исследуемого тела . В этом случае регистрируется излучательность исследуемого тела и по закону Стефана-Больцмана вычисляется его радиационная температура:

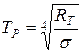
Радиационная температура всегда меньше истинной температуры тела Т. Предположим, что исследуемое тело является серым. Тогда можно записать:

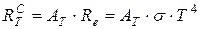
С другой стороны:

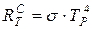
Тогда:

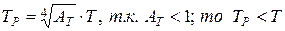
Цветовая температура. Для серых тел (или тел, близких к ним по свойствам) спектральная плотность излучательности равна:

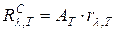
где 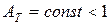. Следовательно, распределение энергии в спектре излучения серого тела такое же, как и в спектре абсолютно черного тела, имеющего такую же температуру. Поэтому к серым телам применим закон Вина, то есть, зная длину волны 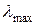, соответствующую максимальной спектральной плотности излучательности 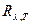исследуемого тела, можно определить его температуру:

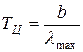
которая называется цветовой температурой.

Для серых тел цветовая температура совпадает с истинной температурой. Для тел, которые сильно отличаются от серых (например, обладающие селективным поглощением), понятие цветовой температурой теряет смысл. Измерением цветовой температуры осуществляется оценка температуры Солнца и звезд.

Яркостная температура. Яркостная температура – температура абсолютно черного тела, при которой для определенной длины волны его спектральная плотность излучательности равна спектральной плотности излучательности исследуемого тела, то есть:

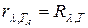(1.13)

где Т – истинная температура тела. По закону Кирхгофа, для исследуемого тела при данной длине волны излучения справедливо:

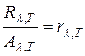
или, учитывая (1.13), получаем:

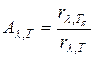
Так как для тел, свойства которых далеки от свойств абсолютно черного тела, 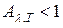, то 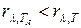, следовательно, 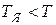, то есть истинная температура всегда выше яркостной.

Несмотря на некоторую неточность в измерении температуры, пирометрические методы имеют значительные преимущества перед прочими методами измерения. Прежде всего, эти методы являются бесконтактными. И, наконец, позволяют производить измерения температуры тел, удаленных от нас на значительные (космические) расстояния.

Фотоэффект

Наряду с законами теплового излучения в конце XIX века было открыто и изучено оптическое явление, не укладывающееся в рамки законов классической физики. Это – явление фотоэлектрического эффекта, или, короче, фотоэффекта. Различают фотоэффект внешний, внутренний и вентильный. Внешним фотоэффектом называют испускание электронов веществом (металлом, полупроводником, диэлектриком) под действием электромагнитного излучения.

В 1887 г. Герц заметил, что ультрафиолетовое излучение в области ис

крового промежутка облегчает разряд. В 1888 г. Гальвакс установил, что причиной этого является появление при облучении свободных зарядов. Первые фундаментальные исследования фотоэффекта выполнены русским ученым А.Г. Столетовым. Принципиальная схема для исследования фотоэффекта приведена на рис.4. Два электрода (катод К из исследуемого материала и анод А – в схеме Столетова применялась металлическая сетка) в вакуумной трубке подключены к батарее так, чтобы с помощью потенциометра R можно изменять не только значение, но и знак подаваемого на них напряжения. Ток, возникающий при освещении катода монохроматическим светом (через кварцевое окошко), измеряется включенным в цепь миллиамперметром. Облучая катод светом различных длин волн, Столетов установил следующие закономерности, не утратившие своего значения до нашего времени:

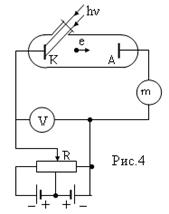-наиболее эффективное действие оказывает ультрафиолетовое излучение;

-под действием света вещество теряет только отрицательные заряды;

-сила тока, возникающего под действием света, прямо пропорциональна его интенсивности.

Томсон (1898 г.) измерил удельный заряд частиц, испускаемых под действием света (по отклонению в электрическом и магнитном полях). Эти измерения показали, что под действием света вырываются электроны.

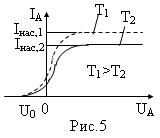На рис.5 приведена вольт-амперная характеристика фотоэффекта – зависимость фототока I_A от напряжения U_A между электродами. Приведенные кривые соответствуют двум разным освещенностям катода (двум различным температурам катода), но одинаковой частоте падающего на катод света. С увеличением напряжения фототок постепенно возрастает, т.е. все большее число фотоэлектронов достигает анода. Из пологого характера кривых следует, что электроны вылетают из катода с разными скоростями. Максимальное значение 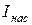– фототок насыщения – определяется таким значением напряжения, при котором все электроны, испускаемые катодом, достигают анода.

Из вольтамперной характеристики следует, что при нулевом значении напряжения фототок не исчезает. Это означает, что электроны, выбитые светом из катода, обладают некоторой начальной скоростью, а значит, и отличной от нуля кинетической энергией и могут достигнуть анода без внешнего поля. Чтобы фототок стал равным нулю, необходимо приложить задерживающее напряжение U₀. При U=U₀ ни один из электронов, даже обладающий при вылете из катода максимальной скоростью V_max,, не может преодолеть задерживающего поля и достигнуть анода. Следовательно,

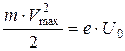(1.14)

Измерив задерживающее напряжение, можно определить максимальные значения скорости и кинетической энергии фотоэлектронов.

Внешний фотоэффект подчиняется следующим трем законам, полученным из обобщения опытных данных: