Физические модели: материальная точка (частица), система материальных точек, абсолютно твердое тело, сплошная среда. Пространство и время

Все окружающие нас тела состоят из ограниченного числа атомов или молекул, то есть представляют собой макроскопические системы.

Механические свойства тел (макросистем) определяются их химическим составом, состоянием, внутренним строением и так далее - это выходит за рамки механики.

В механике для описания движения тел в зависимости от условий конкретных задач используются различные физические модели. Простейшей из них является материальная точка.

Материальной точкой (м.т.)иличастицей называется тело, форма и размеры которого несущественны в данной задаче.

Понятие материальной точки относительно.

Пример. При изучении движения планет вокруг Солнца, их можно принять за материальные точки.

Любое протяженное тело можно разбить на столь большое число частей, что размеры каждой части будут пренебрежимо малы по сравнению с размерами самого тела, т.е. мы имеем еще одну модель - систему материальных точек.

Абсолютным твердым теломназывается тело, расстояние между любыми двумя точками которого всегда остается неизменным, т.е. это система материальных точек, жестко связанных между собой.

Под сплошной средой будем понимать среду с непрерывным распределением массы по объему (в рамках данной задачи).

Все тела существуют и движутся в пространствеи времени. Это основополагающие понятия - наиболее общие формы существования материи.

1.2. Кинематическое описание движения. Система отсчета, радиус-вектор, траектория, радиус кривизны траектории. Поступательное и вращательное движения. Связь линейного и углового перемещений.

Для однозначного определения положения исследуемого тела, в произвольный момент времени, необходимо выбрать систему отсчета.

Системой отсчета называется система координат, снабженная часами и жестко связанная с абсолютно твердым телом (телом отсчета), по отношению к которому определяются положения других тел в различные моменты времени.

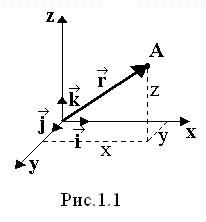В механике наиболее часто используют декартову систему координат. В ней 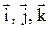- единичные векторы (орты), образующие ортонормированный базис.

Положение материальной точки А, в данный момент времени, задается радиус -

вектором 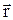(рис. 1.1).

Радиус-вектор материальной точки – вектор, проведенный из начала координат в данную точку: 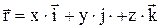, где x,y,z-координаты.

Координаты – расстояния от материальной точки до координатных плоскостей.

Из рисунка 1.1 легко видеть, что модуль радиус-вектора

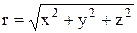
Число независимых координат, полностью определяющих положение тела в пространстве, называется числом степеней свободы.

При движении некоторой материальной точки М, ее координаты и радиус-вектор изменяются с течением времени. Отсюда следует, что для задания закона движения необходимо указать вид функциональных зависимостей от времени всех ее координат.

Зависимости х=х(t), y=y(t), z=z(t) называются скалярными кинематическими уравнениями движения.

Зависимости называются векторными кинематическими уравнениями движения.

Любое произвольное движение тела можно рассматривать как комбинацию поступательного и вращательного движений.

Движение тела называется поступательным, если любая прямая, жестко связанная с телом, остается параллельной своему первоначальному положению.

При вращательном движении точки тела движутся по дугам окружностей, центры которых лежат на одной прямой, называемой осью вращения.

Рассмотрим поступательное движение.

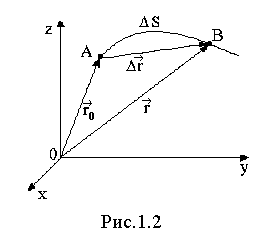Пусть за время t материальная точка из положения А переместилась в положение В (см.рис.1.2).

Траекторией движения точки называется линия, описываемая этой точкой при движении в пространстве, относительно выбранной системы отсчета.

В зависимости от формы траектории различают прямолинейное и криволинейное движения точки.

Длиной путиS ( 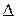S) называется скалярная величина, равная расстоянию, пройденному точкой за рассматриваемый промежуток времени 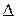t вдоль траектории.

В СИ: длина пути измеряется в метрах.

Вектором перемещения (перемещением) точки за промежуток времени 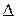t =t - t₀ называется вектор, соединяющий начальное и конечное положения материальной точки (тела).

.

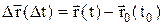Если движение криволинейное, всегда можно выбрать такой минимальный участок траектории, который будет частью какой - то правильной окружности.

Радиус R этой окружности называется радиусом кривизны данного малого участка криволинейной траектории.

Частным случаем криволинейного движения является движение точки по окружности. Радиус кривизны при этом R = const.

Так как при вращательном движении твердого тела все его точки также движутся по дугам окружностей, то для описания вращательного движения твердых тел, также как движения материальной точки по окружности, можно ввести вектор углового перемещения.

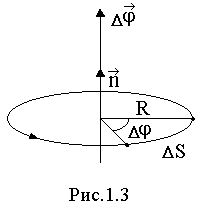Пусть за время 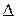t точка перемещается по окружности так, что радиус R поворачивается на угол 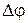.(см.рис.1.3)

Припишем величине 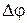направление. Будем считать, что 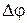направлено вдоль оси вращения точки по правилу правого винта, т.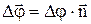е. , где 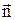- единичный вектор.

Угловое перемещение - вектор, численно равный углу поворота тела, и направленный вдоль оси вращения так, что с его конца поворот виден против часовой стрелки.

В системе СИ угловое перемещение измеряется в радианах [рад].

1.3. Скорость как производная по времени: радиуса-вектора - для поступательного и углового перемещения - для вращательного движений. Связь линейной и угловой скоростей.

Для характеристики направления и быстроты движения в механике вводится векторная физическая величина, называемая скоростью.

а) Поступательное движение

Скорость - векторная физическая величина, характеризующая процесс изменения пространственного положения движущейся материальной точки и равная перемещению, совершаемому точкой за единицу времени.

Различают среднюю и мгновенную скорости.

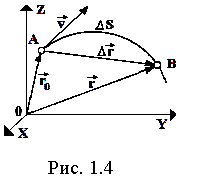
Отношение перемещения 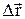(см.рис.1.4), совершенного точкой за промежуток времени 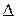t, к этому промежутку времени называется средней скоростью материальной точки за время 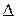t.

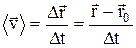. (1.3.1)

Переходя от перемещения к длине пути 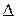S, получим численное значение <v>:

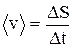. (1.3.2)

Устремим 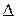t к нулю. Тогда 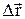, а также и 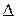S тоже будут стремиться к нулю. При этом оба выше приведенные отношения будут стремиться к определенному пределу.

Мгновенная скорость материальной точки (скорость)– векторная физическая величина, равная первой производной радиус-вектора материальной точки по времени.

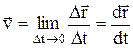. (1.3.3)

Вектор скорости направлен по касательной к траектории движения точки.

В системе СИ скорость измеряется в м/с.

По мере уменьшения t путь S все больше будет приближаться к 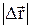, поэтому модуль мгновенной скорости

.

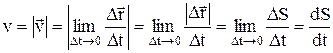Таким образом, модуль мгновенной скорости материальной точки равен первой производной пути по времени:

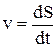(1.3.4)

б) Вращательное движение.

При вращательном движении тела изменяется со временем угловое перемещение. Следовательно, аналогично поступательному движению можно ввести угловую скорость как характеристику быстроты изменения углового перемещения тела.

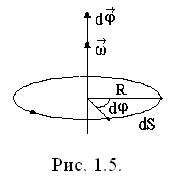
Угловой скоростью называется векторная величина 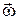, равная первой производной углового перемещения по времени:

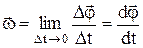(1.3.5).

Очевидно, что 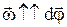. В системе единиц СИ угловая скорость измеряется в рад/с.

Несложно, исходя из введенных ранее определений, получить связь линейной и угловой скоростей:

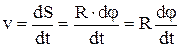
Используя соотношение (1.3.5), получим:

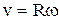. (1.3.6)

При постоянной угловой скорости 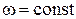, можно ввести период и частоту вращения.

Время Т, за которое тело совершает полный оборот, называется периодом вращения.

Число полных оборотов за единицу времени называетсячастотой вращения.

Частоту и период можно связать с угловой скоростью вращения.

Пусть 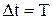, тогда 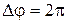и, следовательно, по определению .

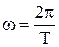Тогда 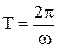, , 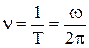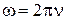(1.3.7).