Истинная и средняя теплоемкости
Теплоемкость является функцией параметров состояния – давления и температуры, поэтому в технической термодинамике различают истинную и среднюю теплоемкости.
Теплоемкость идеального газа зависит только от температуры и по определению может быть найдена лишь в интервале температур 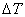 . Однако всегда можно предположить, что этот интервал очень мал вблизи какого-либо значения температуры. Тогда можно сказать, что теплоемкость определена при данной температуре. Такая теплоемкость называется истинной.
. Однако всегда можно предположить, что этот интервал очень мал вблизи какого-либо значения температуры. Тогда можно сказать, что теплоемкость определена при данной температуре. Такая теплоемкость называется истинной.
В справочной литературе зависимость истинных теплоемкостей ср и сv от температуры задают в виде таблиц и аналитических зависимостей. Аналитическую зависимость (например, для массовой теплоемкости) обычно представляют в виде полинома:

Тогда количество подведенной в процессе теплоты в интервале температур [t1,t2] определяется интегралом:
 . (2)
. (2)
При исследовании термодинамических процессов часто определяют среднее в интервале температур значение теплоемкости. Она представляет собой отношение количества подведенной в процессе теплоты Q12 к конечной разности температур:
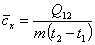 . (3)
. (3)
Тогда, если задана зависимость истинной теплоемкости от температуры, в соответствии с (2):
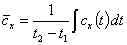 .
.
Часто в справочной литературе приводят значения средних теплоемкостей ср и сv для интервала температур от 0 доtоС. Как и истинные, их представляют в виде таблиц и функций:
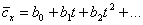 (4)
(4)
При подстановке значения температуры t в эту формулу будет найдена средняя теплоемкость в интервале температур [0,t]. Чтобы найти среднее значение теплоемкости в произвольном интервале [t1,t2], пользуясь зависимостью (4), нужно найти количество теплоты Q12, подведенной к системе в этом интервале температур. На основании известного из математики правила интеграл в уравнении (2) может быть разбит на следующие интегралы:
 .
.
Но
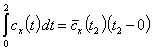 , а
, а  .
.
Тогда
 .
.
После этого искомое значение средней теплоемкости находят по формуле (3).
Газовые смеси
В технике в качестве рабочих тел чаще используются не чистые вещества, а смеси различных газов. Под газовой смесью в данном случае понимают механическую смесь чистых веществ, называемых компонентами смеси, не вступающих друг с другом в химические реакции. Примером газовой смеси является воздух, основными компоненты которого являются кислород и азот. Если компонентами смеси являются идеальные газы, то и смесь в целом также будем считать идеальным газом.
При рассмотрении смесей предполагается, что:
- каждый газ, входящий в состав смеси, равномерно распределён по всему объёму, то есть его объём равен объёму всей смеси;
- каждый из компонентов смеси имеет температуру, равную температуре смеси;
- каждый газ создаёт своё давление на стенки сосуда, называемое парциальным давлением.
Парциальное давление, таким образом, это давление, которое имел бы компонент смеси, если бы он один занимал весь объем смеси при той же температуре. Сумма парциальных давлений каждого компонента равна давлению смеси (закон Дальтона):
 .
.
Парциальным объёмом компонента V 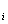 называется такой объём, который занимал бы данный компонент при давлении, равном давлению смеси, и температуре, равной температуре смеси. Очевидно, что сумма парциальных объемов равна объему смеси (закон Амага):
называется такой объём, который занимал бы данный компонент при давлении, равном давлению смеси, и температуре, равной температуре смеси. Очевидно, что сумма парциальных объемов равна объему смеси (закон Амага):
 .
.
При исследовании термодинамических процессов с газовыми смесями необходимо знать ряд характеризующих их величин: газовую постоянную, молярную массу, плотность, теплоемкость и т.д. Для их нахождения должен быть задан состав смеси, определяющий количественное содержание каждого компонента, входящего в смесь. Состав газовой смеси обычно задают массовыми, объёмными или мольными долями.
Массовой долей компонента смеси g 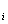 называется величина, равная отношению массы компонента к массе всей смеси:
называется величина, равная отношению массы компонента к массе всей смеси:
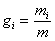 .
.
Очевидно, что масса смеси m равна сумме масс всех компонентов:
 ,
,
а сумма массовых долей:
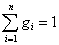 .
.
Объемной долей компонента смеси ri называется величина, равная отношению парциального объема компонента к объему смеси:
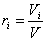 .
.
Уравнение объёмного состава смеси имеет вид:




и сумма объемных долей:
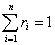 .
.
 Мольной долей компонента смеси хi называется величина, равная отношению числа молей этого компонента к общему числу молей смеси:
Мольной долей компонента смеси хi называется величина, равная отношению числа молей этого компонента к общему числу молей смеси:
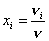 .
.
Очевидно, что:
 .
.
Состав смеси задают долями единицы или в процентах. Связь между мольными и объемными долями можно установить, записывая уравнение Клапейрона – Менделеева для компонента смеси и всей смеси:
 ,
,
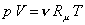 .
.
Поделив почленно первое уравнение на второе, получим:
 .
.
Таким образом, для идеальных газов объемные и мольные доли оказываются равными.
Связь между массовыми и объёмными долями устанавливается соотношениями:
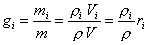 . (5)
. (5)
Из закона Авогадро следует:
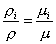 , (6)
, (6)
где μ – молярная масса смеси, которую называют кажущейся. Она может быть найдена, в частности, через объемный состав смеси. Записывая уравнение Клапейрона – Менделеева для i-го компонента смеси в виде

и суммируя по всем компонентам, получим:
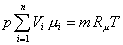 .
.
Сравнивая его с уравнением состояния для смеси в целом
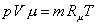 ,
,
приходим к очевидному соотношению:
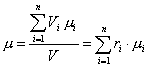 .
.
Если найдена молярная масса смеси, газовая постоянная смеси может быть определена обычным способом:
 . (7)
. (7)
Газовую постоянную смеси можно рассчитать и через массовые доли и газовые постоянные компонентов. Запишем для каждого компонента смеси уравнение Клапейрона:
 .
.
Суммируя по всем компонентам, получим:
 .
.
Сумма в левой части уравнения равна объему смеси. Поделив обе части уравнения на массу смеси m
 ,
,
замечаем, что сумма в правой части уравнения представляет собой газовую постоянную смеси:
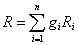 .
.
С учетом (6) и (7) соотношение (5) можно дополнить:
 .
.
Используя последнее соотношение

и производя суммирование по компонентам
 ,
,
получим расчетную формулу для газовой постоянной смеси через объемные доли:
 .
.
Удельный объем и плотность смеси и компонентов можно найти из уравнений состояния:
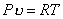 и
и 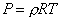 ,
,
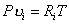 и
и 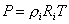 .
.
В соответствии с определениями парциального давления и парциального объема можно записать:
 .
.
Тогда парциальное давление компонента смеси:
 .
.
Расчет теплоёмкости газовой смеси выполняют на основе данных о составе смеси и теплоёмкости каждого компонента. Массовая, объемная и мольная теплоемкости смеси рассчитываются через соответствующие доли:
- массовая теплоемкость
 ;
;
- объемная теплоемкость
 ;
;
- мольная теплоемкость
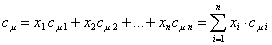 .
.
Этими формулами пользуются при определении истинных и средних теплоемкостей смеси.
