Первый закон Ньютона. Масса. Сила

Динамика является основным разделом механики, в ее основе лежат три закона Ньютона, сформулированные им в 1687 г. Законы Ньютона играют исклю­чительную роль в механике и являются (как и все физические законы) обобщени­ем результатов огромного человеческого опыта. Их рассматривают как систему взаимосвязанных законов и опытной про­верке подвергают не каждый отдельный закон, а всю систему в целом.

Первый закон Ньютона:всякая мате­риальная точка (тело) сохраняет состоя­ние покоя или равномерного прямолиней­ного движения до тех пор, пока воздейст­вие со стороны других тел не заставит ее изменить это состояние.

Стремление тела сохранять состояние покоя или равномерного прямолинейного движения называется инертностью.По­этому первый закон Ньютона называют также законом инерции.

Механическое движение относительно, и его характер зависит от системы отсче­та. Первый закон Ньютона выполняется не во всякой системе отсчета, а те системы, по отношению к которым он выполняется, называются инерциальными системами от­счета.Инерциальной системой отсчета яв­ляется такая система, которая либо по­коится, либо движется равномерно и прямолинейно относительно какой-то другой инерциальной системы. Первый закон Ньютона утверждает существование инерциальных систем отсчета.

Опытным путем установлено, что инерциальной можно считать гелиоцентрическую (звездную) систему отсчета (начало координат находится в центре Солнца, а оси проведены в направлении определенных звезд). Система отсчета, связанная с Землей, строго говоря, неинерциальна, однако эффекты, обусловлен­ные ее неинерциальностью (Земля враща­ется вокруг собственной оси и вокруг Со­лнца), при решении многих задач прене­брежимо малы, и в этих случаях ее можно считать инерциальной.

Из опыта известно, что при одинако­вых воздействиях различные тела неоди­наково изменяют скорость своего движе­ния, т. е., иными словами, приобретают различные ускорения. Ускорение зависит не только от величины воздействия, но и от свойств самого тела (от его мас­сы).

Масса тела - физическая величина, являющаяся одной из основных характе­ристик материи, определяющая ее инерци­онные (инертная масса) и гравитацион­ные (гравитационная масса)свойства. В настоящее время можно считать дока­занным, что инертная и гравитационная массы равны друг другу (с точностью, не меньшей 10^-12 их значения).

Для описания воздействия одного тела на другое вводится понятие силы. Сила – это векторная величина, которая является мерой воздействия на тело других тел или полей, в результате которого тело приобретают ускорения или изменяют форму и размеры (т.е. деформируется). Обозначается сила буквой .

2.2. Основной за­кон динамики поступательного движе­ния.

Основной за­кон динамики поступательного движе­ния отвечает на вопрос, как изменяет­ся механическое движение материальной точки (тела) под действием приложен­ных к ней сил.

Если рассмотреть действие различных сил на одно и то же тело, то оказывается, что ускорение, приобретаемое телом, всег­да прямо пропорционально равнодейст­вующей приложенных сил:

a ~ F (m = const). (2.1)

При действии одной и той же силы на тела с разными массами их ускорения оказываются различными, а именно:

a ~ 1/m (F = const). (2.2)

Используя выражения (2.1) и (2.2) и учи­тывая, что сила и ускорение — величины векторные, можем записать

. (2.3)

Соотношение (2.3) выражает второй закон Ньютона:ускорение, приобретаемое материальной точкой (телом), пропорцио­нально вызывающей его силе, совпадает с нею по направлению и обратно пропорционально массе материальной точ­ки (тела).

В СИ коэффициент пропорциональности k = 1. Тогда

,

или

. (2.4)

Учитывая, что масса материальной точки (тела) в классической механике есть величина постоянная, в выражении (2.4) ее можно внести под знак производной:

. (2.5)

При переменной массе из (2.5) имеем

. (2.5')

Векторная величина

, (2.6)

численно равная произведению массы ма­териальной точки на ее скорость и име­ющая направление скорости, называется импульсом (количеством движения)этой материальной точки.

Подставляя (2.6) в (2.5), получим

. (2.7)

Эта формула выражает основной за­кон динамики поступательного движе­ния:скорость изменения импульса материальной точки равна действующей на нее силе.

Единица силы в СИ - Ньютон (Н):1 Н - сила, которая массе в 1 кг сообща­ет ускорение 1 м/с² в направлении дейст­вия силы:

1 Н = 1 кг·м/с².

Второй закон Ньютона справедлив только в инерциальных системах отсчета. Первый закон Ньютона можно получить из второго. Действительно, в случае ра­венства нулю равнодействующей сил (при отсутствии воздействия на тело со стороны других тел) ускорение (см. (2.3)) также равно нулю. Однако первый закон Ньюто­на рассматривается как самостоятельный закон (а не как следствие второго зако­на), так как именно он утверждает существование инерциальных систем отсче­та, в которых только и выполняется урав­нение (2.7).

В механике большое значение имеет принцип независимости действия сил: если на материальную точку действует одно­временно несколько сил, то каждая из этих сил сообщает материальной точке ускорение согласно второму закону Ньютона, как будто других сил не было. Согласно этому принципу, силы и ускоре­ния можно разлагать на составляющие, использование которых приводит к су­щественному упрощению решения задач. Например, на рис. 2.1 действующая сила разложена на два компонента: тангенциальную силу (направлена по касательной к траектории) и нормальную силу 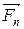(направлена по нормали к центру кривизны). Используя выражения а_τ = и a_n = , а также υ= Rω, можно записать:

F_τ = mа_τ = m , (2.8)

F_n = ma_n = mυ²/R = mω² R. (2.9)

Если на материальную точку действует одновременно несколько сил, то, согласно принципу независимости действия сил, под во втором законе Ньютона понимают результирующую силу: .

Третий закон Ньютона

Взаимодействие между материальными точками (телами) определяется третьим законом Ньютона: всякое действие мате­риальных точек (тел) друг на друга носит характер взаимодействия силы, с которы­ми действуют друг на друга материальные точки, всегда равны по модулю, противо­положно направлены и действуют вдоль прямой, соединяющей эти точки:

, (2.10)

где - сила, действующая на первую материальную точку со стороны второй; - сила, действующая на вторую мате­риальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

Третий закон Ньютона позволяет осу­ществить переход от динамики отдельной материальной точки к динамике системы материальных точек. Это следует из того, что и для системы материальных точек взаимодействие сводится к силам парного взаимодействия между материальными точками.

Силы в механике

Обсуждая до сих пор силы, мы не интере­совались их происхождением. Однако в механике мы будем рассматривать раз­личные силы: трения, упругости, тяготе­ния.

а) Силы трения. Из опыта известно, что всякое тело, движущееся по горизонтальной поверхно­сти другого тела, при отсутствии действия на него других сил с течением времени замедляет свое движение и в конце концов останавливается. Это можно объяснить существованием силы трения, которая препятствует скольжению соприкасаю­щихся тел друг относительно друга. Различают внешнее (сухое) и внутрен­нее (жидкое или вязкое) трение. Внешним трением называется трение, возникающее в плоскости касания двух соприкасающих­ся тел при их относительном перемещении. Если соприкасающиеся тела неподвижны друг относительно друга, говорят о трении покоя, если же происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения говорят о трении скольжения, качения или верчения.

Обсудим некоторые закономерности внешнего трения. Это трение обусловлено шероховатостью соприкасающихся повер­хностей; в случае же очень гладких по­верхностей трение обусловлено силами межмолекулярного притяжения.

Рассмотрим лежащее на плоскости те­ло (рис. 2.2), к которому приложена горизонтальная сила . Тело придет в движе­ние лишь тогда, когда приложенная сила будет больше силы трения . Француз­ские физики Г. Амонтон и Ш. Кулон опытным путем установили следующий закон: сила трения скольжения F_тр пропорциональна силе F_N нормального давления, с которой одно тело действует на другое:

F_тр = μ F_N , (2.11)

где μ - коэффициент трения скольжения, зависящий от свойств соприкасающихся поверхностей.

Для гладких поверхностей определенную роль играет межмолекулярное притяжение. В этом случае закон трения скольжения имеет вид

F_тр = μ_ист(F_N +Sp₀),

где p₀- добавочное давление, обус­ловленное силами межмолекулярного при­тяжения, которые быстро уменьшаются с увеличением расстояния между частица­ми; S - площадь контакта между телами; μ_ист - истинный коэффициент трения скольжения.

Трение играет большую роль в при­роде и технике. Благодаря трению движет­ся транспорт, удерживается забитый в стену гвоздь и т. д.

В некоторых случаях силы трения ока­зывают вредное действие, и поэтому их надо уменьшать. Для этого на трущиеся поверхности наносят смазку (сила трения уменьшается примерно в 10 раз), которая заполняет неровности между этими повер­хностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости. Таким образом, внешнее трение твердых тел заменяется значительно мень­шим внутренним трением жидкости.

Радикальным способом уменьшения силы трения является замена трения скольжения трением качения (шариковые и роликовые подшипники и т.д.).

б) Упругие силы. Под действием внешних сил возникают деформации (т. е. изменения размеров и формы) тел. Если после прекращения действия внешних сил восстанав­ливаются прежние форма и размеры тела, то дефор­мация называется упругой. Деформация имеет упругий характер в случае, если внешняя сила не превосходит определенного значения, которое назы­вается пределом упругости. При превышении этого предела деформация становится пластиче­ской. В этом случае после устранения внешних сил первоначальные форма и размеры тела полностью не восстанавливаются. В дальнейшем мы будем рассматривать только упругие деформации.

В деформированном теле возникают упругие силы, которые уравновешивают внешние силы, вызвавшие деформацию. Поясним это на примере деформации пружины. Под действием внешней силы пружина получает удлинение х, в результате чего в ней возникает упругая сила , уравновешивающая силу .

Упругие силы возникают во всей деформированной пружине. Любая часть пружины действует на другую часть с силой, равной .

Установленный экспериментально закон Гука утверждает, что при упругой деформации удлинение пружины пропорционально внешней силе. Аналитически эту закономерность принято записывать следующим образом:

.

Величина k называется жест­костью пружины. Из этого выражения следует, что чем больше k, тем меньшее удлинение получает пружина под действием данной силы.

Упругая сила отличается от внешней только знаком. Поэтому F_упр,x = - F_внеш,x и, следовательно,

.

Опустим для краткости индекс «упр» и напишем это соотношение в виде
F_x = - kx , (2.12)

где F_x - проекция упругой силы на ось х, k - жест­кость пружины, х - удлинение пружины.

в) Силы тяжести и всемирного тяготения. И. Ньютон, изучая дви­жение небесных тел, на основании законов Кеплера и основных законов динамики открыл всеобщий закон всемирного тя­готения: между любыми двумя материаль­ными точками действует сила взаимного притяжения, прямо пропорциональная произведению масс этих точек (m₁ и m₂) и обратно пропорциональная квадрату расстояния между ними (r²):

F = G m₁m₂ /r². (2.13)

Эта сила называется гравитационной (или силой всемирного тяготения). Силы тяго­тения всегда являются силами притяже­ния и направлены вдоль прямой, проходя­щей через взаимодействующие тела. Ко­эффициент пропорциональности G на­зывается гравитационной постоянной.

Закон всемирного тяготения установ­лен для тел, принимаемых за материальные точки, т. е. для таких тел, размеры кото­рых малы по сравнению с расстоянием между ними. Если же размеры взаимодей­ствующих тел сравнимы с расстоянием между ними, то эти тела надо разбить на точечные элементы, подсчитать силы притяжения между всеми попарно взятыми элементами, а затем гео­метрически их сложить (проинтегрировать), что является довольно сложной ма­тематической задачей.

На любое тело, расположенное вблизи Земли, действует сила тяготения F, под влиянием которой, согласно второму за­кону Ньютона, тело начнет двигаться с ускорением свободного падения g. Та­ким образом, в системе отсчета, связанной с Землей, на всякое тело массой m дей­ствует сила

, (2.14)

называемая силой тяжести.

Согласно фундаментальному физиче­скому закону - обобщенному закону Га­лилея, все тела в одном и том же поле тяготения падают с одинаковым ускорени­ем. Следовательно, в данном месте Земли ускорение свободного падения одинаково для всех тел.

Если пренебречь суточным вращением Земли вокруг своей оси, то сила тяжести и сила гравитационного тяготения равны между собой:

F_Т = mg = G mM /R², (2.15)

где М - масса Земли; R - расстояние между телом и центром Земли. Эта форму­ла дана для случая, когда тело находилось вблизи поверхности Земли.

Если тело расположено на высоте h от поверхности Земли, R₀ - радиус Зем­ли, тогда

F_Т = G mM /(R₀ + h)², (2.16)

т. е. сила тяжести с удалением от повер­хности Земли уменьшается.

В физике применяется также понятие веса тела. Весом тела называют силу, с которой тело вследствие тяготения к Земле действует на опору (или подвес), удерживающую тело от свободного паде­ния. Вес тела проявляется только в том случае, если тело движется с ускорением, отличным от , т. е. когда на тело кроме силы тяжести действуют другие силы. Со­стояние тела, при котором оно движется только под действием силы тяжести, на­зывается состоянием невесомости.

Таким образом, сила тяжести действует всегда, а вес появляется только в том случае, когда на тело кроме силы тяжести действуют еще другие силы, вследствие чего тело движется с ускорением , отлич­ным от . Если тело движется в поле тяготения Земли с ускорением ≠ ,то к этому телу приложена дополнительная сила , удовлетворяющая условию

.

Тогда вес тела
, (2.17)

т. е. если тело покоится или движется прямолинейно и равномерно, то = 0 и . Если тело свободно дви­жется в поле тяготения по любой траекто­рии и в любом направлении, то = и = 0, т. е. тело будет невесомым. Например, невесомыми являются тела, находящиеся в космических кораблях, сво­бодно движущихся в космосе.