Задания для практической части занятия. Практическое занятие № 7

Практическое занятие № 7

Первое и второе начала термодинамики

Цель: Обобщение и закрепление теоретического материала по теме «Первое и второе начала термодинамики. Термодинамика изопроцессов» и рассмотрение решения задач по данной теме.

Требования к исходному уровню знаний и умений

Знать определения следующих физических понятий:

Ø Внутренняя энергия;

Ø Степени свободы молекулы;

Ø Равновесные и неравновесные процессы;

Ø Адиабатный процесс;

Ø Обратимый и необратимый термодинамические процессы;

Ø Круговой процесс (или цикл);

Ø Прямой и обратный цикл;

Ø Термодинамическая вероятность состояния системы;

Ø Тепловой двигатель;

Ø Холодильная машина

Знать определения следующих физических величин, уметь записать формулы, которыми они определяются, указать единицы измерения и значения.

Ø Внутренняя энергия для произвольной массы т газа;

Ø Теплоемкость;

Ø Удельная теплоемкость вещества;

Ø Молярная теплоемкость;

Ø Теплоемкость при постоянном объеме;

Ø Теплоемкость при постоянном давлении;

Ø Показатель адиабаты (или коэффициент Пуассона);

Ø Термический коэффициент полезного действия для кругового процесса;

Ø Энтропия;

Ø Изменение энтропии идеального газа;

Ø Изменение энтропии в изопроцессах.

Знать формулировку, уметь записать формулы, определяющие следующие физические законы:

Ø Закон равномерного распределения энергии по степеням свободы молекулы;

Ø Первое начало термодинамики;

Ø Применение первого начала термодинамики к изопроцессам (изохорному, изотермическому, изобарному, адиабатному);

Ø Второе начало термодинамики (закон возрастания энтропии);

Ø Третье начало термодинамики (теорема Нернста — Планка);

Ø Статистическое истолкование третьего начала термодинамики.

Уметь записать формулу полной работы, совершаемую газом при изменении его объема, и изобразить ее графически.

Уметь записать уравнение Майера и знать его физический смысл.

Уметь записать уравнение адиабатного процесса (уравнение Пуассона).

Уметь изобразить графически прямой или обратный цикл и записать, чему равна работа, совершаемая за этот цикл.

Уметь изобразить графически цикл Карно и назвать процессы, входящие в этот цикл.

Уметь записать и пояснить неравенство Клаузиуса.

Сведения из теории

Средняя полная кинетическая энергия молекулы

,

где i – число степеней свободы молекулы.

Молярная теплоёмкость газа при постоянном объёме и постоянном давлении соответственно

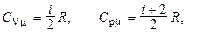
где i – число степеней свободы; R – универсальная газовая постоянная.

Связь между удельной (с) и молярной (С_m) теплоёмкостями

С_m = сm

где m – молярная масса.

Уравнение Майера

С_рm – С_Vm = R.

Внутренняя энергия идеального газа

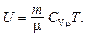
Уравнение адиабатного процесса (уравнение Пуассона)

pV ^g = const, TV ^g-1 = const, T^gp^1-g = const,

где g – показатель адиабаты,

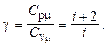
Работа, совершаемая газом при изменении его объёма, в общем случае вычисляется по формуле

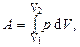
где V₁ и V₂ – начальный и конечный объемы газа.

Работа при изобарном процессе (р = const)

A = p (V₂ – V₁),

при изотермическом (Т = const) –

при адиабатном (Q = const) –

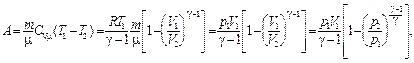
где Т₁, Т₂, V₁, V₂, p₁, p₂ – соответственно, начальные и конечные температура, объём и давление газа.

Первое начало термодинамики

Q = DU + A,

где Q – количество теплоты, сообщённое газу; DU – изменение его внутренней энергии; А – работа, совершённая газом против внешних сил.

Первое начало термодинамики при изобарном процессе

при изохорном (А = 0 ) –

при изотермическом (DU = 0) –

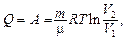
при адиабатическом (Q = 0) –

Термический коэффициент полезного действия для кругового процесса (цикла)

где Q₁ – количество теплоты, полученное системой; Q₂ – количество теплоты, отданное системой; А – работа, совершаемая за цикл.

КПД цикла Карно

где Т₁ – температура нагревателя; Т₂ – температура холодильника.

Холодильный коэффициент машины, работающей по обратному циклу Карно,

где Q₂ – количество теплоты, отведённое из холодильной камеры; А – совершённая работа; Т₂ – температура более холодного тела (холодильной камеры); Т₁ – температура более горячего тела (окружающей среды).

Изменение энтропии при равновесном переходе системы из состояния 1 в состояние 2

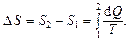
Изменение энтропии идеального газа

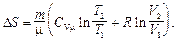
Неравенство Клаузиуса:

.

Согласно Больцману, энтропия системы и термодинамическая вероятность связаны между собой следующим образом:

,

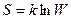где k — постоянная Больцмана.

Теорема Нернста — Планка:

.

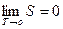Задания для практической части занятия

1. Найти среднюю кинетическую энергию <ε_вр> вращательного движения одной молекулы кислорода при температуре Т = 286 К, а также кинетическую энергию W_вр вращательного движения всех молекул этого газа, если его масса 4 г.

2. Определите кинетическую энергию <ε₁>, приходящуюся в среднем на одну степень свободы молекулы азота, при температуре Т = 1000К, а также <ε_п> среднюю кинетическую энергию поступательного движения, <ε_вр> вращательного движения и <ε> среднее значение полной кинетической энергии молекулы.

3. Определить количество теплоты, поглощаемой водородом массой m = 0,2 кг при нагревании его от температуры t₁ = 0 ºC до температуры t₂ = 100 ºC при постоянном давлении. Найти также изменение внутренней энергии газа и совершаемую им работу.

4. Кислород объемом 1 л находится под давлением 1 МПа. Определите, какое количество теплоты необходимо сообщить газу, чтобы 1) увеличить его объем вдвое в результате изобарного процесса; 2) увеличить его давление вдвое в результате изохорного процесса.

5. Некоторый газ массой 1 кг находится при температуре Т = 300 К и под давлением р₁ = 0,5 МПа. В результате изотермического сжатия давление газа увеличилось в два раза. Работа, затраченная на сжатие, А = 432 кДж. Определите: 1) какой это газ; 2) первоначальный удельный объем газа.

6. Работа расширения некоторого двухатомного идеального газа составляет А = 1 кДж. Определите количество подведенной к газу теплоты, если процесс протекал: 1) изотермически; 2) изобарно.

7. При адиабатном расширении кислорода (ν = 2 моль), находящегося при нормальных условиях, его объем увеличился в n = 3 раза. Определите: 1) изменение внутренней энергии газа; 2) работу расширения газа.

8. Азот массой m = 1 кг занимает при температуре Т₁ = 300 К объем V₁ = 0,5 м³. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определите: 1) конечный объем газа; 2) его конечную температуру; 3) изменение внутренней энергии газа.

9. Идеальный двухатомный газ, содержащий количество вещества ν = 1 моль, находится под давлением р₁ = 250 кПа и занимает объем V₁ = 10 л. Сначала газ изохорически нагревают до Т₂ = 400К. Далее изотермически расширяя, доводят его до первоначального давления. После этого путем изобарического сжатия возвращают газ в начальное состояние. Определить термический КПД цикла.

10. Нагреватель тепловой машины, работающий по обратному циклу Карно, имеет температуру t₁ = 200ºС. Определить температуру Т₂ охладителя, если при получении от нагревателя количества теплоты Q₁= 1 Дж машина совершает работу А = 0,4 Дж? Потери на трение и теплоотдачу не учитывать.

11. Определить изменение ΔS энтропии при изотермическом расширении кислорода массой m = 10 г от объема V₁ = 25 л до объема V₂ = 100 л.

12. Найти изменение ΔS энтропии при нагревании воды массой m = 100 г от температуры t₁ = 0ºС до температуры t₂ = 100ºС и последующем превращении воды в пар той же температуры (удельная теплоемкость с = 4,18·10³ Дж/(кг·К), удельная теплота парообразования λ = 22,6·10⁵ Дж/кг)

13. Считая азот идеальным газом, определить его удельную теплоемкость 1) для изохорного процесса; 2) для изобарного процесса.

14. Некоторый газ при нормальных условиях имеет удельный объем 0,7 м³/кг. Определите удельные теплоемкости с_v и с_р этого газа.

15. Определите удельные теплоемкости с_v и с_р смеси углекислого газа массой m₁ = 3 г и азота массой m₂ = 4 г.

16. Определите показатель адиабаты для смеси газов, содержащей гелий массой m₁ = 8 г и водород массой m₂ = 2 г.

17. Кислород объемом 1л находится под давлением 1МПа Определите какое количество теплоты необходимо сообщить газу, чтобы: 1) увеличить его объем вдвое в результате изобарного процесса; 2) увеличить его давление вдвое в результате изохорного процесса.

18. Некоторый газ массой 1кг находится при температуре Т = 300К и под давлением р₁ = 0,5 МПа. В результате изотермического сжатия давление газа увеличилось в два раза. Работа, затраченная на сжатие, А = - 432кДж. Определите: 1) какой это газ; 2) первоначальный удельный объем газа.

19. При нагревании двухатомного идеального газа ( v = 2 моль) его термодинамическая температура увеличилась в 2 раза. Определите изменение энтропии, если нагревание происходит: 1) изохорно; 2) изобарно.

20. Идеальный газ совершает цикл Карно, термический КПД которого равен 0,4. Определите работу изотермического сжатия, если работа изотермического расширения составляет 400Дж.

ОТВЕТЫ:

№1. <ε_вр> = 3,94·10^-21 Дж; W_вр = 296 Дж.

№2 1) <ε₁> = 6,9·10^-21Дж; 2) <ε_п> = 20,7·10^-21Дж; 3) <ε_вр> = 13,8·10^-21Дж; 4) <ε> = 34,5·10^-21Дж

№3. Q = 291 кДж; ΔU = 208 кДж; А = 83 кДж.

№4. 1) Q₁ = 3,5 кДж; 2) Q₂ = 2,5 кДж.

№5. 1) гелий; 2) v₁ = 1,25 м³/кг.

№6. 1) Q₁ = 1 кДж; 2) Q₂ = 3,5 кДж.

№7. 1) ΔU = -4,03 кДж; 2) А = 4,03 кДж.

№8. 1) V₂ = 0,228 м³; 2) Т₂ = 411 К; 3) ΔU = 82,4 кДж.

№9. η = 0,041.

№10. Т₂ = 284 К.

№11. ΔS = 3,6 Дж/К.

№12 ΔS = 737 Дж/К.

№13. 1) с_v = 742 Дж/(кг·К); 2) с_р = 1,04 кДж/(кг·К).

№14. 1) с_v = 649 Дж/(кг·К); 2) с_р = 909 Дж/(кг·К); кислород.

№15. 1) с_v = 667 Дж/(кг·К); 2) с_р = 917 Дж/(кг·К);

№16.γ = 1,55

№17. 1) Q₁ = 3,5 кДж; 2) Q₂ = 2,5 кДж.

№18 1) гелий; 2) v₁ = 1, 25 м³/ кг.

№19 1) ΔS₁ = 28,8 Дж/К; 2) ΔS₂= 40,3 Дж/К

№20 А ₃₄= -240 кДж.