Потенциальный баpьеp. Туннельный эффект

Различие в поведении квантовых и классических частиц проявляется в том случае, если на пути частицы встречается потенциальный барьер (при 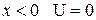, при )

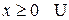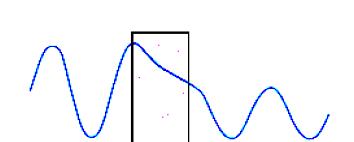
При 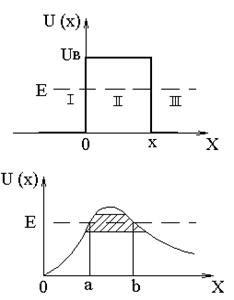данных условиях задачи классическая частица, обладая Е (полная энергия частицы), либо беспрепятственно пройдет над барьером (при E > U), либо отразится от него (при E < U) и будет двигаться в обратную сторону. Для микрочастицы же, даже при 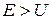, имеется отличная от нуля вероятность, что она отразится от барьера. При 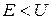имеется также отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Подобные выводы следуют из решения уравнения Шредингера для стационарных состояний. Рассмотрим случай 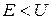, тогда для областей 1 и 3 имеем

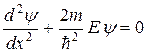
для области 2

.

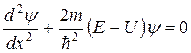Общие решения этих дифференциальных уравнений:

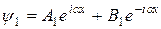(для области 1)

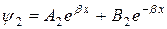(для области 2)

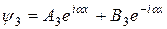(для области 3)

где , .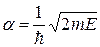

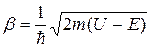Решение вида 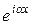соответствует волне, распространяющейся в положительном направлении оси х, а решение вида - волне, распространяющейся в противоположном направлении. В области 3 имеется только волна, прошедшая сквозь барьер и распространяющаяся слева направо. Поэтому коэффициент 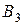следует принять равным нулю. Для нахождения остальных коэффициентов воспользуемся условиями, которым должна удовлетворять функция y. Для того чтобы y была непрерывна во всей области изменений х от - ¥ до + ¥, должны выполняться условия: 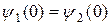и . Для того чтобы y была гладкой, т.е. 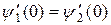не имела изломов, должны выполняться условия: и .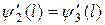

Отношение квадратов модулей амплитуд отраженной и падающей волны

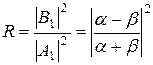(7.11)

определяет вероятность отражения частицы от потенциального барьера и называется коэффициентом отражения.

Отношение квадратов модулей амплитуд прошедшей и падающей волны

определяет вероятность прохождения частицы через барьер и называется коэффициентом прохождения (прозрачности). Для барьера конечной ширины

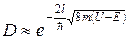(7.12)

В случае барьера произвольной формы

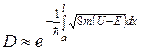
При преодолении потенциального барьера частица как бы проходит через «туннель» в нем, в связи с чем данное явление называется туннельным эффектом. С классической точки зрения туннельный эффект представляется абсурдным, так как частица в туннеле должна была бы обладать отрицательной кинетической энергией 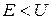. Однако туннельный эффект – явление специфически квантовое. В квантовой же механике деление полной энергии на кинетическую и потенциальную не имеет смысла, так как противоречит соотношению неопределенностей.

Различие в поведении квантовых и классические частиц проявляется в том случае если на пути частицы встречается потенциальная ступень 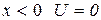(при , при )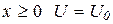

Для классической частицы: если Е – полная энергия частицы меньше U₀ то она не преодолеет и, потеряв часть скорости, будет двигаться вдоль Х.

Для квантовой частицы: если 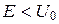,она проникнет на некоторую глубину, а затем начнет двигаться обратно.

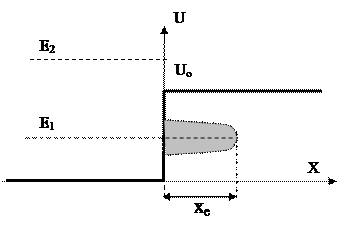Глубиной проникновения . при которой вероятность нахождения частицы уменьшается в е раз

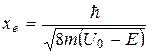
Например, металлическое тело для свободных электронов является потенциальной ямой с U₀, которая выше Е электрона на 1 эВ. Тогда 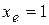Å.

Поверхность металла является потенциальным барьером, который электроны преодолевают на глубину 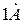и возвращаются обратно. Следовательно, поверхность металла окружена облаком электронов

В 1922 г. было открыто явление холодной электронной эмиссии (автоэмиссия) из ме 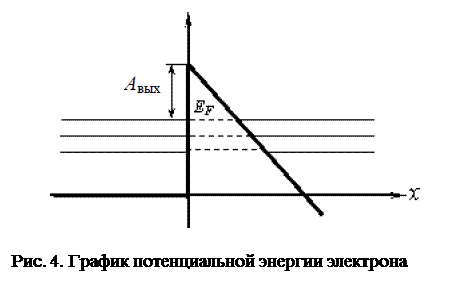таллов под действием сильного внешнего электрического поля. Отрицательные значения координаты х (рис. 4) – это область металла,в котором электроны могут двигаться почти свободно. Здесь потенциальную энергию можно считать постоянной. На границе металла возникает потенциальная стена, не позволяющая электрону покинуть металл. Он может это сделать, лишь приобретя добавочную энергию, равную работе выхода А_вых. При низкой температуре такую энергию может получить только ничтожная доля электронов. Если сделать металл отрицательной пластиной конденсатора, приложив к нему достаточно мощное электрическое поле, то потенциальная энергия электрона из-за его отрицательного заряда вне металла начнет уменьшаться.

Классическая частица не проникнет через такой потенциальный барьер. Сразу после появления квантовой механики Фаулер и Нордгейм объяснили явление холодной эмиссии с помощью туннельного эффекта для электронов. Электроны внутри металла имеют самые разные энергии даже при температуре абсолютного нуля, так как согласно принципу Паули в каждом квантовом состоянии может быть не больше одного электрона (с учетом спина). Поэтому число заполненных состояний равно числу электронов, а энергия самого верхнего заполненного состояния E_F – энергия Ферми – в обычных металлах составляет величину порядка нескольких электронвольт так же, как и работа выхода.

Легче всего будут туннелировать электроны с энергией E_F, с уменьшением энергии вероятность туннелирования резко падает. Все экспериментальные особенности, а также полная величина эффекта описываются формулой Фаулера – Нордгейма. Холодная электронная эмиссия – первое явление, успешно объясненное туннелированием частиц.

Туннельный эффект играет большую роль в электронных приборах.

Он обусловливает протекание таких явлений, как эмиссия электронов под

действием сильного поля, прохождение тока через диэлектрические плёнки,

пробой p–n-перехода; на его основе созданы туннельные диоды, разрабаты-

ваются активные плёночные элементы.

Сканирующие туннельные микроскопы созданы на основе туннельного эффекта.