Розділ 2. Принципи спеціальної теорії відносності. 5 страница

1) ПВЕ справедливий для усіх фізичних теорій (крім теорій гравітації) у той час як справедливість ПВГ обмежена нерелятивістською механікою (як класичної так і квантової);

2) хоча й у ПВЕ й у ПВГ однаково фундаментальну роль грає поняття ІСВ, однак зв'язок між різними ІСВ здійснюється з допомогою принципу різних перетворень - перетворень Лоренца (утримуючих фундаментальну постійну "с"; безліч таких перетворень в математичному відношенні утворять групу Лоренца) і перетворень Галілея (вони утворять групу Галілея), відповідно.

Зауваження 2. В другому постулаті СТВ найбільш важливим є його перша частина, тобто твердження про незалежність швидкості світла у вакуумі від руху джерела в одній заданій (фіксованої) ИСВ. Саме це твердження суперечить "здоровому глузду", тому що в механіці ми прийшли б до протилежного твердження на основі нерелятивістського закону додавання швидкостей (див. частина I, §…). Друга ж частина постулату, що затверджує однаковість швидкості світла у всіх ІСВ, є простий наслідок ПВЕ і рівнянь Максвела: дійсно, з рівнянь Максвела випливає, що в деякої ІСВ швидкість світла у вакуумі дорівнює "с"; тоді в силу ПВЕ вона повинна дорівнювати "с" і у всіх інших ІСВ (тому що всі ІСВ рівноправні).

Зауваження 3. У СТВ фундаментальну роль грає поняття інерціальної системи відліку. При цьому мається на увазі, що ІСВ завжди можна вводити і використовувати глобально, тобто для вивчення фізичних явищ у будь-яких просторових і часових масштабах. При цьому завжди явно чи неявно ми користаємося еквівалентністю різних точок простору і часу, тобто однорідністю часу й однорідністю і ізотропністю простору. Таким чином, використання у фізичній теорії поняття ІСВ має на увазі використання двох постулатів:

1) час однорідний;

2) простір однорідний і ізотропний.

Помітимо, що тільки спільне використання цих постулатів СТВ дозволяє побудувати СТВ як логічно замкнуту фізичну теорію. У частині III цього курсу ми побачимо, що при врахуванні гравітаційного поля простір утрачає властивості однорідності і ізотропності, а час - властивість однорідності. Це означає, що при вивченні гравітаційних явищ уже неможливо використовувати звичне поняття глобальної ІСВ й отже потрібно істотно змінити (узагальнити) спеціальний ПВЕ (у теорії гравітації відповідний принцип відносності ми будемо називати загальним принципом відносності на противагу спеціальному принципу відносності СТВ; відповідно до цього і Ейнштейнівска теорія гравітації одержала назву загальної теорії відносності на противагу спеціальної теорії відносності, досліджуваної в цій главі).

Виберемо тепер дві ІСВ- 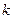і , що рухаються відносно один одного з деякою постійною швидкістю 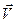так, як зазначено на малюнку (8.1) (див також частина I, §…).

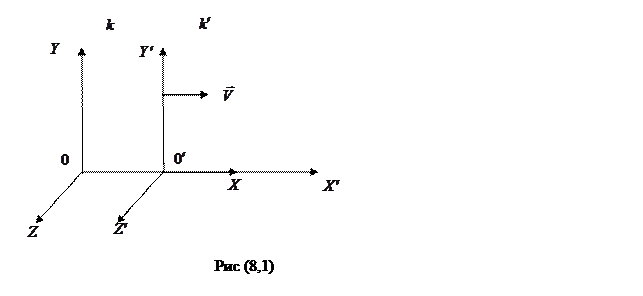
Розглянемо довільне точкове миттєве фізичне явище (наприклад, миттєвий спалах точкового джерела світла), що надалі ми будемо називати фізичною подією чи просто подією, з погляду систем відліку 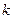і . Нехай 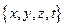- позначення координат і часу цієї події в системі 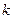, а 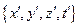– у системі . Установимо зв'язок між цими часовими-тимчасовими-просторово-тимчасовими характеристиками події - це й означає знайти правила переходу від системи 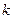до системи (і навпаки), тобто установити перетворення Лоренца.

Послідовне використання постулатів СТВ і постулатів про однорідність часу й однорідності ізотропності простору дозволяє вивести (довести) перетворення Лоренца (так як цей доказ приводиться в багатьох посібниках, то ми його тут опускаємо):

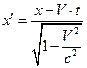
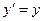
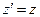(8.1)

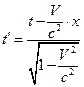
Ці перетворення іноді називають умовно "прямими" перетвореннями Лоренца. Іноді для застосувань необхідно знати зворотну залежність 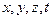від 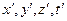. Вона легко одержується рішенням системи (8.1) відносно :

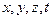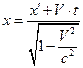
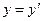(8.2)

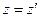
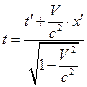
Перетворення (8.2) умовно можна назвати "зворотними" перетвореннями Лоренца.

При 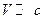, тобто при малих відноснихшвидкостях двох ІСВ перетворення Лоренца (8.1) чи (8.2) переходить у відповідні перетворення Галілея. Таким чином, перетворення Галілея - це граничний випадок перетворень Лоренца. Це означає, перетворення Галілея тільки приблизно відбивають реальні часово-просторові відносини фізичного світу, для більш точного опису яких необхідно використовувати перетворення Лоренца і наслідки з них.