Система аксіом і правил виведення
Класична математична логіка
Розділ 4
Аксіоматичні системи логік
Аналогічно числення висловлювань в аксіоматичній системі логік існує формальна система – числення предикатів, що займається конструюванням формул і доведенням їх загальнозначущості. Числення предикатів, тобто формальна теорія предикатів, будується за вищенаведеною класичною схемою побудови формальних теорій.
Аксіоматична система логік має ідентичну численню висловлювань структуру: мову, систему аксіом і правила виведення. Мова аксіоматичної системи логік складається з правильно побудованих формул логіки предикатів першого порядку, а опис аксіом і правил виведення наведений у наступному параграфі.
Система аксіом і правил виведення
Числення предикатів першого порядку визначають аксіоматичним шляхом. Аксіоми поділяють на два класи: логічніаксіоми і власні аксіоми, абонелогічні аксіоми. До логічних аксіом відносять аксіоми, що визначаються для будь-яких А, В, С схемами:
АП1) А→ (В → А);
АП2) (А → (В → С)) → ((А → В) → (А → С));
АП3) ( 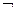 В → А) → ((
В → А) → (( 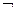 В → А) → В);
В → А) → В);
АП4) 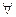 х1А(х1) → А(t), де t – терм, вільний для змінної х1 у формулі А(х1);
х1А(х1) → А(t), де t – терм, вільний для змінної х1 у формулі А(х1);
АП5) 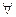 х1 (А → В) → (А →
х1 (А → В) → (А → 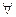 х1В), якщо формула А не містить вільних входжень змінної х1.
х1В), якщо формула А не містить вільних входжень змінної х1.
Власні аксіоми, будучи визначеними, фіксують деяку конкретну теорію першого порядку, тому для спільного описання всіх теорій першого порядку вони не можуть бути сформульованими. Якщо власних аксіом немає, то таку теорію називають численням предикатів першого порядкуі позначають ПL.
У численні предикатів першого порядку визначено два основні правила виведення:
П1) modus ponens(МР): із А і А→В випливає В;
П2) правило узагальнення: із А випливає 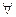 хі А.
хі А.
Поняття виведення із множини формул у теорії ПLвизначають аналогічно численню висловлювань, але при цьому необхідно внести додаткове уточнення. Воно полягає в тому, що у виведенні формули В із множини формул Г змінна xi є фіксованою, якщо в цьому виведенні жодного разу не застосовувалося правило П2 узагальнення за змінною 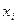 . У протилежному разі кажуть, що змінна
. У протилежному разі кажуть, що змінна 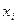 у даному виведенні варіюється.
у даному виведенні варіюється.
Для позначення факту наявності виведення формули В із множини формул Г, в якому всі змінні, xj,…xjz фіксовані, використовують запис Г ├ 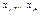 В. Інакше кажучи, у цьому записі указують, що правило узагальнення використовують тільки за змінними xj,…, xjz.
В. Інакше кажучи, у цьому записі указують, що правило узагальнення використовують тільки за змінними xj,…, xjz.
Приклад 4.1.1.Вивести формулу А( а0, х2) із формули А(х1, х2).
Розв’язання.Для виведення формули застосуємо правило узагальнення й із А(х1, х2) одержимо 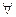 х1 А(х1, х2). Згідно з аксіомою АП4 запишемо аксіому
х1 А(х1, х2). Згідно з аксіомою АП4 запишемо аксіому
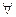 x1 А(х1, х2)→А(х0, х2). (4.1.1)
x1 А(х1, х2)→А(х0, х2). (4.1.1)
Одержана формула 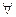 х1 А(х1, х2) разом із 4.1.1 за МР дозволяє вивести А( а0,х). У побудованому виведенні змінна х1 варіюється. Тоді виведення формули можна записати у такому вигляді: А(х1, х2) ├
х1 А(х1, х2) разом із 4.1.1 за МР дозволяє вивести А( а0,х). У побудованому виведенні змінна х1 варіюється. Тоді виведення формули можна записати у такому вигляді: А(х1, х2) ├ 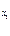 А1 (
А1 ( 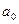 ,
, 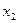 ).
).
Як зазначалося вище, в логіці предикатів першого порядку визначені два основні правила виведення: П1), П2), але з розділів 1 і 2 можна зробити висновок, що для можливості скорочення довжини виведення необхідно роз-ширити множину правил виведення. Розглянемо деякі з них, які можуть бути застосовані при виведенні формул у логіці предикатів першого порядку.
Їх можна розділити на дві групи. До першої відносять такі структурні правила виведення.
1. Закон тотожності
А ├ А
2. Правило введення, що формулюється так: якщо Г ├ А, то Г, В ├ А. Для наочності його, а в подальшому й усі інші, будемо записувати у вигляді
 Г ├ А
Г ├ А
Г, В├ А
3. Правило перестановки
Г, В, С, ∆├ А
 Г, С, В ,∆ ├ А
Г, С, В ,∆ ├ А
4. Правило скорочення
Г, В, В, ∆├ А
 Г, В, ∆├ А
Г, В, ∆├ А
5. Правило перетину
 Г├ ∆, А├ В
Г├ ∆, А├ В
Г, ∆├ С
До другої групи відносять логічні правила виведення, які, у свою чергу, можна розбити на групи, для яких є логічні зв’язки і квантори зі своєю групою правил. Крім того, всередині кожної групи правила ділять на два види: правила введення, що показують доведення формули з даним логічним символом, і правила вилучення, що показують використання формули з даним логічним символом для доведення інших формул.
1. Правило диз’юнкції:
введення вилучення


 Г├ А . Г├ В . Г, А ├ С; Г, В ├ С
Г├ А . Г├ В . Г, А ├ С; Г, В ├ С
Г├ А 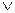 В ’ Г├А
В ’ Г├А 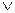 В Г, А
В Г, А 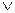 В ├ С ˙
В ├ С ˙
2. Правило кон’юкції:
введення вилучення
Г ├ А; Г ├ В Г, А, В ├ С

 Г ├ А
Г ├ А 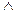 В ’ Г, А
В ’ Г, А 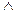 В ├ С ˙
В ├ С ˙
3. Правило імплікації:
введення вилучення

 Г,А├В Г├ А; Г ├ А → В Г ├ А → В Г ├ В
Г,А├В Г├ А; Г ├ А → В Г ├ А → В Г ├ В
4. Правило еквівалентності:
введення вилучення
Г, А ├ В; Г, В ├ А Г ├; Г ├ А ~ В

 Г ├ А ~ В
Г ├ А ~ В  Г ├ В
Г ├ В
Г ├ В; Г ├ А ~ В
 Г├А ˙ 5. Правило заперечення:
Г├А ˙ 5. Правило заперечення:
введення вилучення
 Г, А ├ В; Г, А ├
Г, А ├ В; Г, А ├ 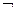 В Г ├
В Г ├ 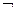
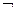 А
А
 Г ├
Г ├ 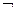 А Г ├ А ˙ 6. Правило узагальнення:
А Г ├ А ˙ 6. Правило узагальнення:
введення вилучення

 Г ├ А (у) Г ├
Г ├ А (у) Г ├ 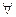 хА(х)
хА(х)
Г ├ 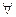 х А (х) Г ├ А (у)
х А (х) Г ├ А (у)
У формулі введення квантора загальності А (у) означає для довільного у 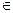 F, а саме правило стверджує істинність
F, а саме правило стверджує істинність 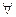 х А (х), якщо доведена істинність А (у) для будь-якого у, тобто для всіх елементів у з розглянутої пред-метності області F.
х А (х), якщо доведена істинність А (у) для будь-якого у, тобто для всіх елементів у з розглянутої пред-метності області F.
У формулі видалення квантора загальності А (у) означає для довільного у 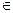 F, а саме правило використовується для доведення істинності А (у), де у – довільно обраний елемент предметної області F, у якій справедливе
F, а саме правило використовується для доведення істинності А (у), де у – довільно обраний елемент предметної області F, у якій справедливе
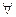 х А (х).
х А (х).
7. Правило існування:
введення вилучення

 Г├ А (у) . Г,
Г├ А (у) . Г, 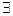 х А (х) ├ С
х А (х) ├ С
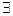 х А (х) Г, А (у) ├ С ˙ У формулі вилучення квантора існування А (у) означає для деякого у
х А (х) Г, А (у) ├ С ˙ У формулі вилучення квантора існування А (у) означає для деякого у 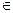 F, а саме правило дозволяє вирішити, що
F, а саме правило дозволяє вирішити, що 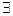 х А (х) єістинним тоді і тільки тоді, коливідомий деякий елемент у, для якого істинне А (у).
х А (х) єістинним тоді і тільки тоді, коливідомий деякий елемент у, для якого істинне А (у).
У формулі вилучення квантора існування А (у) означає для деякого у 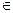 F, а саме правило полягає в позначенні імені елемента у, для якого А (у) є істинне.
F, а саме правило полягає в позначенні імені елемента у, для якого А (у) є істинне.
Усі розглянуті вище правила відповідають звичайним прийомам математичного міркування. Наприклад, у правилі існування вилучення квантора 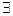 відповідає правилу одиничного вибору. Припустимо, що є
відповідає правилу одиничного вибору. Припустимо, що є 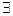 х А (х) і необхідно вивести С. Оскільки є х таке, що А (х), то можна розглянути (вибрати) одне із таких х. Позначимо його через у. Це означає, що для цього у дійсне А (у). Таким чином, достатньо вивести формулу С із А (у). Аналогічно можна розглянути й інші правила.
х А (х) і необхідно вивести С. Оскільки є х таке, що А (х), то можна розглянути (вибрати) одне із таких х. Позначимо його через у. Це означає, що для цього у дійсне А (у). Таким чином, достатньо вивести формулу С із А (у). Аналогічно можна розглянути й інші правила.
