Знаходження ймовірностей випадкових подій. Умова нормування

Поняття випадкової події “А” і ймовірність W”А” появи цієї події

У фізиці взагалі, та в молекулярній фізиці зокрема, доводиться постійно мати справу з випадковими подіями. Випадковими подіями (випадковими значеннями x_i фізичної величини x) називають такі події, факт появи яких наперед з достовірністю передбачити неможливо. На питання, чи буде мати місце дана подія чи ні, неможливо дати визначену відповідь.

Приклад:

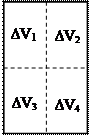У посудині знаходиться газ. Подумки розіб’ємо даний об’єм на 4 рівні частини: DV₁, DV₂, DV₃, DV₄. Вкинемо до посудини “мічену” (радіоактивну) молекулу, знаходження якої можливо визначити приладами, і будемо слідкувати за її місцезнаходженням у об’ємі посудини. Будемо фіксувати, наприклад, таку подію “А”, як знаходження молекули в об’ємі DV₂ через кожні 5 хвилин. Чи можливо заздалегідь дати точну відповідь на питання, чи буде через 15 хвилин після початку спостереження знайдена молекула в об’ємі DV₂? Певної відповіді на це питання дати неможливо. Бо молекули в газі рухаються хаотично. Тому знаходження молекули в даному об’ємі – подія випадкова. Іншими словам: координати x, y, z окремої молекули – величини випадкові. Теж саме можливо сказати і стосовно швидкостей u_x, u_y, u_z. Передбачити їхнє точне значення неможливо.

Крім того що координати і швидкості окремих молекул x_i, u_i є величинами випадковими (приймають випадкові значення), вони ще несуттєві для усієї сукупності молекул в цілому, бо ніяк не характеризують властивостей всієї системи молекул.

Знаходження ймовірностей випадкових подій. Умова нормування

Разом з тим, випадкові події (значення випадкових величин) підкоряються статистичним закономірностям, які відображають властивості усієї системи молекул в цілому і тому носять об’єктивний характер. Як нам вже відомо, якщо подія “А” випадкова, то це означає, що неможливо достовірно наперед визначити – здійсниться ця подія чи ні. Однак є можливість наперед визначити наскільки велика ймовірність! появи тієї чи іншої події “А”.

Нехай при проведенні N дослідів (спостережень) випадкова подія “А” була зафіксована при N_А дослідах. Збільшення числа проведених експериментів до нескінченності призводить до прагнення відносної частоти 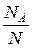спостереження випадкової події “А” до границі:

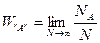(1)

де W_”А” - імовірність появи випадкової події “А”. Це частотне визначення імовірності. Вважається, що кількість дослідів складає достатньо велике число і знак lim опускають:

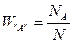(1*)

Імовірність W_”А” може приймати значення в інтервалі 0£ W_”А”£1. Значення W_”А”=0 відповідає випадкові, коли при жодному досліді не спостерігається подія “А” – неможлива подія. Відповідно імовірність W_”А” = 1 можлива тільки тоді, коли при усіх дослідах спостерігалася тільки подія “А” – достовірна подія.

Приклад:

Повернемося до спостереження за “міченою” молекулою в об’ємі V. Фіксуємо подію “А”, яка полягає в тому, що “мічена” молекула потрапляє в об’єм DV₂. Для цього протягом тривалого періоду часу t будемо знаходити положення частинки через проміжки часу Dt. Тоді число вимірювань дорівнює 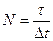. Нехай за час t частинка проводить усередині малого об'єму DV₂ час t_А, тоді число "позитивних вимірювань" буде рівним:

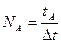
Ймовірність того, що частинка знаходиться в об’ємі DV₂, визначається:

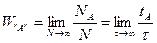
Якщо час спостереження досить великий, то час перебування t_А ~ DV₂, тоді ймовірність буде рівною:

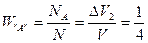
Такі ж ймовірності будемо фіксувати і для знаходження “міченої” молекули в об’ємі DV₁ – подія “В”, DV₃ – подія “С”, DV₄ – подія “D”.

; ;

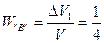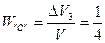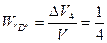
Сума ж усіх цих ймовірностей дорівнює:

W = W_”А”+W_”В”+W_”С”+W_”D” =1 (2)

Формула (2) і є умовою нормування ймовірності випадкових подій. По-суті, це ймовірність виявити “мічену” молекулу в якій-небудь частині об’єму V, який займає газ.

В загальному випадку виконується умова:

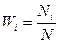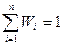Þ (3)

Словами умову нормування ймовірностей W_i взаємно виключаючих подій (і =1, 2,…, n) можна виразити наступним чином: сума ймовірностей усіх можливих (для досліджуваної системи) взаємно виключаючих подій дорівнює одиниці. Взаємно виключаючи події – це такі події, коли поява однієї з них, виключає появу усіх інших.