Частица в одномерной яме с абсолютно непроницаемыми стенками

Рассмотрим одно из проявлений чисто квантовой природы электрона. Известно, что волны различной физической природы, возбуждаемые в ограниченном объеме, имеют строго определенную длину волны и частоту. В том случае, когда движение электрона происходит в ограниченной области, егоэнергия имеет строго определенные, дискретные значения. Говорят, что спектр энергий квантован. Если электрон заперт в атоме, молекуле или любой потенциальной яме, то волновая функция Ψ представляет стоячую волну. Если речь идет о прямоугольной потенциальной яме, которая изображена на рис. 2, то по своей форме волна будет такой же, как и в случае натянутой струны. Однако, во-первых, природа волны здесь иная, а во-вторых, дискретным в этом случае будет не спектр частот, а спектр энергий.

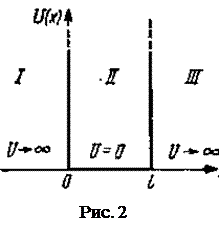
Рассмотрим частицу в одномерной прямоугольной потенциальной яме с бесконечно высокими непроницаемыми стенками. Потенциальная энергия в этом случае удовлетворяет условиям

,

,

.

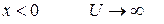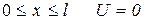Поскольку частица может двигаться только вдоль оси х уравнение Шредингера для стационарных состояний примет вид

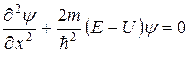
За пределами ямы вероятность обнаружить частицу равна нулю. Следовательно, и 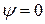. Из условий непрерывности на границах ямы

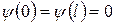
Для частицы в яме уравнение Шредингера имеет вид

.

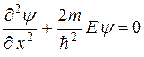Обозначим 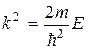. Для уравнения 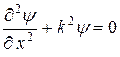общим решением является 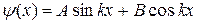. Так как 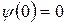, то B = 0 и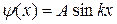

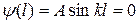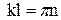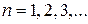Условие выполняется только при , где (при 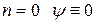получается, что частица отсутствует).

Тогда 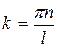. Выразив из 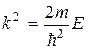энергию, получим:

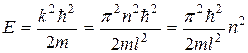
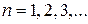(7)

Спектр энергии оказался дискретным. Квантованные значения энергии 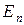называются уровнями энергии, а число n, определяющее энергетические уровни частицы, главным квантовым числом. Квантово-механическое рассмотрение данной задачи приводит к выводу, что частица в потенциальной яме не может иметь энергию меньшую чем 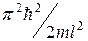при n = 1. Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей.

Если рассчитать расстояние между соседними уровнями энергии, в качестве частицы взяв электрон 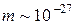г, то для ямы шириной ~ 10 см (свободные электроны в металле) получим 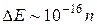эВ. То есть, чем больше m и l, тем гуще располагаются уровни энергии, так что спектр практически можно считать непрерывным и квантование энергии на характере движения частиц сказываться не будет. Если же размеры ямы l ~ 10^-9м – 10^-8м (1 нм – 10 нм), то для электрона 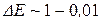эВ и получаются явно дискретные значения энергии.

Найдем собственные функции

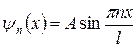
Для нахождения А воспользуемся условием нормировки

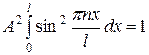
В результате интегрирования получим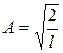

Откуда 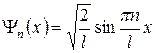( 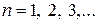) (8)

Графики собственных функций даны на рис.3

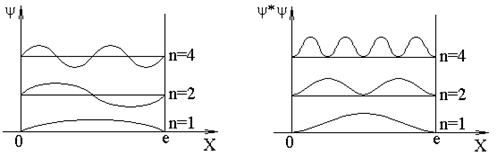
Из рис.3 следует, что, например, в квантовом состоянии n = 2 частица не может находиться в середине ямы, в то время как одинаково часто может пребывать в ее левой и правой частях. Такое поведение частицы, очевидно, несовместимо с представлением о траектории.

Видно, что электронная плотность в яме распределяется неравномерно, есть максимумы и минимумы плотности вероятности. Также следует, что длины волн Ψ-функций, описывающих электронные состояния с различными n, удовлетворяют условиям λn/2 = a/n, т. е. в яме укладывается целое число полуволн.

Примером структуры с двумерным электронным газом являются тонкие пленки. В такой структуре одно из направлений (z) очень мало, следовательно, энергетический спектр в этом направлении можно описать формулой (7), так как в данном направлении образуется потенциальная яма. В оставшихся двух направлениях электроны могу передвигаться свободно. Образованную потенциальную яму надо считать бесконечно глубокой, следовательно, E_n должны быть малы по сравнению с действительной глубиной ямы. Данное условие приводит к толщине пленки порядка нанометров, что соответствует нескольким межатомным расстояниям. Полная энергия носителей в квантово-размерной пленке носит смешанный дискретно-непрерывный спектр: E = E_n+ (p_x² + p_y²)/2m, где p_x и p_y – компоненты импульса в плоскости слоя.

Производство таких тонких пленок в явном виде весьма проблематично. Однако в настоящее время эффекты наблюдают на гетероструктурах (контакты между полупроводниками с различной шириной запрещенной зоны). На таком контакте края энергетических зон испытывают скачки, ограничивающие движение носителей и играющие роль стенок квантовой ямы.

В структуре с одномерным электронным газом два направления (y и z) очень малы, следовательно, энергетический спектр в каждом направлении можно описать формулой (7), где l – толщина пленки в данном направлении, так как в этом направлении образуется потенциальная яма. В оставшемся направлении (x) электроны могут передвигаться свободно. Образованную потенциальную яму надо считать бесконечно глубокой, следовательно, E_n должны быть малы по сравнению с действительной глубиной ямы. Данное условие приводит к толщине нити порядка нанометров. Полная энергия носителей в квантоворазмерной нити, аналогично тонким пленкам, носит смешанный дискретно-непрерывный спектр: E = E_n + E_m + p_x²/2m, где p_x – компонента импульса в направлении нити (x).

В структуре с нульмерным электронным газом все направления (x, y и z) очень малы, следовательно, энергетический спектр в каждом направлении

можно описать формулой (7), где l – толщина пленки в данном направлении, так как в этом направлении образуется потенциальная яма. Образованную потенциальную яму надо считать бесконечно глубокой, следовательно, E_n должны быть малы по сравнению с действительной глубиной ямы. Данное условие приводит к размеру точки порядка нанометров. Полная энергия носителей квантовой точки имеет дискретный спектр: E = E_n + Е_m + Е_k. Такие структуры особенно интересны тем, что их свойства аналогичны свойствам дискретного атома, поэтому их иногда называют искусственными атомами.

Эффект размерного квантования (ЭРК) – явление, связанное с квантованием энергии носителей заряда, движение которых ограничено в одном, двух или трех направлениях.

(ЭРК называют также квантовым ограничением, т.к.электронные свойства наноразмерных структур отличаются от известных объемных свойств материала, из которого они сделаны.)

При ограничении бесконечного кристалла потенциальными барьерами или при создании границ возникают дискретные уровни квантования. В принципе, дискретный спектр возникает в любом ограниченном потенциальными стенками объёме, но практически наблюдается только при достаточно малом размере тела.

Типичным примером ЭРК может служить двойная гетероструктура AlGaAs/GaAs/AlGaAs с двумерным электронным газом, где электроны, находящиеся в слое GaAs, ограничены высокими потенциальными барьерами AlGaAs, т. е. для электронов формируется потенциальная яма, описываемая дном зон проводимости двух материалов, малого размера (обычно порядка 10 нм) и возникают дискретные уровни, которые соответствуют движению электронов поперёк слоя GaAs, хотя продольное движение остаётся свободным. Эти уровни эффективно сдвигают зону проводимости вверх по энергии. В результате изменяется ширина запрещённой зоны GaAs и соответственно происходит сдвиг в синюю область края межзонного поглощения. Аналогич но, но с большим изменением запрещённой зоны ЭРК наблюдается в квантовых точках, где электрон ограничен по всем трём координатам.

Туннелирование

80 лет назад наш соотечественник Г. А. Гамов впервые получил решения уравнения Шредингера, описывающие возможность преодоления частицей энергетического барьера даже в случае, когда энергия частицы меньше высоты барьера (она как будто проходит через туннель). Новое явление, называемое туннелированием, позволило объяснить многие экспериментально наблюдавшиеся процессы. Найденное решение позволило понять большой круг явлений и было применено для описания процессов, происходящих при вылете частицы из ядра – основы атомной науки и техники.

Развитие электроники подошло к использованию процессов туннелирования лишь почти 30 лет спустя: появились туннельные диоды, открытые японским ученым Л. Есаки, удостоенным за это открытие Нобелевской премии. Еще через 5 лет Ю. С. Тиходеев, руководивший сектором физико-теоретических исследований в Московском НИИ «Пульсар», предложил первые расчеты параметров и варианты использования приборов на основе многослойных туннельных структур, позволяющих достичь рекордных по быстродействию результатов. Спустя 20 лет они были успешно реализованы.

В настоящее время процессы туннелирования легли в основу технологий, позволяющих оперировать со сверхмалыми величинами порядка нанометров.