Московский авиационный институт

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ

(национальный исследовательский университет)» (МАИ)

Факультет № 1: «Испытания летательных аппаратов»

Кафедра № Б12: «Информационные технологии испытаний и управления»

Утверждено на заседании

редакционного совета

Протокол №

от «____»________20__­_г.

Методические рекомендации по выполнению практической работы №1 по дисциплине:

«Автоматизация испытаний»

Тема: «Первичные преобразования сообщений. Теорема Котельникова»

для основной образовательной программы:

«Испытание летательных аппаратов»

по специальности 162110

Разработано:

Ассистент Мирошникова Е.Н.

Утверждено

на заседании кафедры Б12-ИТИиУ

«13» мая 2014 г.

(протокол № 13 (81) )

Введение

Переход от аналогового представления сигнала к цифровому дает значительные преимущества при хранении, передаче и обработке информации, повышается точность и надежность работы радиоканала, увеличивается объем передаваемой информации при сохранении требуемой точности. Кроме того, дискретизация по времени позволяет использовать одни и те же устройства (каналы связи, устройства обработки информации) для большого числа различных сигналов.

1 Дискретизация по времени

При дискретизации (квантовании) по времени непрерывная функция заменяется совокупностью мгновенных значений X(t_k), к=0, 1, 2, …..n,т.е преобразуется в функцию дискретного аргумента. Временной интервал 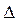t=t_k –t_k-1 между двумя соседними фиксированными моментами времени, в которых задается дискретная функция называется интервалом (шагом) квантования. Величина, обратная интервалу квантования, называется частотой квантования: f_k=1/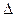t.

Методы временной дискретизации аналоговой информации делятся на методы равномерной и неравномерной дискретизации. При равномерной дискретизации X(t) на всем рассматриваемом диапазоне его изменения частота дискретизации f_k (и соответственно интервал между дискретными отчетами 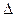t) остается постоянными.

В случае неравномерной дискретизации интервал между отчетами изменяется в зависимости от изменения характеристик измеряемых процессов. Такая дискретизация называется адаптивной.

В реальных системах сбора и передачи информации дискретный процесс всегда отражает исходный измеряемый процесс с некоторой погрешностью. В общем случае под погрешностью дискретизации понимают погрешность, с которой может быть восстановлен непрерывный процесс по его дискретным значениям. Отсюда следует, что наиболее важным при проведении дискретизации является вопрос правильного выбора шага дискретизации (или, что то, же частоты квантования). Известно несколько критериев для выбора частоты квантования. Рассмотрим основные из них.

1.1 Критерий Котельникова

В.А. Котельниковым доказана теорема для временной дискретизации функций с ограниченным спектром. Любая непрерывная функция X(t), спектр которой ограничен частотой F_c , полностью определяется последовательностью своих дискретных значений в моменты времени, отстоящие друг от друга на интервал

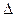t=1/(2F_c) (1)

В соответствии с теоремой непрерывную функцию можно представить в виде ряда Котельникова:

X(t)= 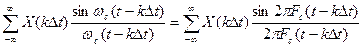, (2)

где X(k 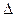t)- отсчеты функции в моменты времени t_k;

w_c- круговая частота, соответствующая граничной частоте спектра F_c ;

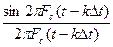- система ортогональных функций, называемых функциями отсчетов.

Sa(y)

Из формулы ряда Котельникова следует, что функция с ограниченным спектром имеет бесконечную протяженность во времени и состоит из суммы бесконечно большого числа членов, каждый из которых представляет собой одну и ту же функцию вида: , но с различными постоянными коэффициентами X(k 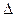t). Эти коэффициенты равны значениям исходной непрерывной функции X(t) в моменты отсчета. График функции имеет вид:

1

3Dt

2Dt

Dt

-Dt

-2Dt

-3Dt

0 t

Рисунок 1. График функции отсчетов

Таким образом, если известны значения функции X(t) в точках отсчета k 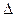t, то она может быть полностью восстановлена для всех моментов времени посредством суммирования типовых функций отсчетов с соответствующими коэффициентами.

1.2 Восстановление непрерывного сигнала по его дискретным отсчетам

Пусть k=0, тогда ряд Котельникова примет вид:

=

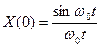для k=1

для k=2 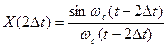и т.д.

Для восстановления непрерывного сигнала, в каждой точке отсчета, по формуле Котельникова нужно построить функцию отсчетов, и затем все эти функции сложить (рисунок 2).

В самих точках отсчета все кривые, кроме одной, равны нулю. В промежуточных точках складывается бесконечное множество ординат от всех графиков.

Функция отсчетов Sa(у) представляет собой реакцию идеального фильтра нижних частот на 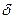-функцию. Граничная частота фильтра должна быть равна max частоте, которой ограничен спектр сигнала, т.е. F_c (или w_c). Следовательно, если в приемном устройстве поместить такой фильтр и подавать на него последовательность идеально узких импульсов с амплитудой, соответствующей значениям непрерывной функции в точках отсчета X(k 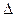t), и следующих друг за другом с периодом 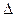t, то на выходе фильтра мы получим исходную непрерывную функцию.

-3Dt

-2Dt

4Dt

3Dt

2Dt

Dt

-Dt

Sa(y)

X(0Dt)

X(1Dt)

t

X(2Dt)

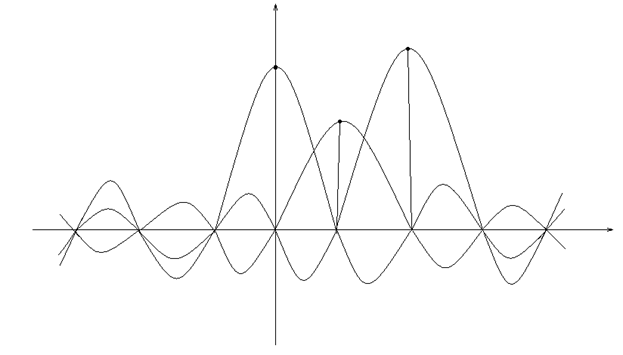
Рисунок 2

Однако при практическом применении теоремы Котельникова возникает ряд принципиальных затруднений:

1. Всякий реальный сигнал имеет конечную длительность, т.е. функция X(t) ограничена по аргументу t, а с помощью ряда Котельникова она представляется состоящей из суммы функций отсчетов, имеющих бесконечную протяженность во времени. Если же функция X(t) ограничена по времени, то спектр её будет бесконечно широким, а это противоречит основному условию теоремы Котельникова.

2. Для восстановления сигнала в промежуточных точках нужно знать как все предыдущие, так и последующие значения функций отсчетов. Такие идеальные фильтры физически нереализуемы.

3. Бесконечное суммирование неосуществимо, поэтому, хотя теоретически ошибок восстановления нет, но на практике ряд конечен и это приводит к ошибкам.

1.3 Дискретизация сигналов с неограниченным спектром

Рассмотрим вопрос квантования по времени реальных сигналов, имеющих неограниченный спектр (рисунок 3)

S(f)

-f 0 f

Рисунок 3. Спектр реального сигнала

Функция S(f) ® 0, но нулём не становится. Площадь под кривой есть дисперсия сигнала s²

Если применить к такому сигналу теорему Котельникова, то для F=¥, интервал дискретизации Dt получается равным нулю. Таким образом, при дискретизации реальных сигналов обязательно будут невосстанавливаемые потери информации. Поэтому задачу дискретизации можно ставить только так:

Исходя из заданной точности выбрать интервал Dt.

Если реальный сигнал приближённо заменить сигналом с ограниченным спектром, то при этом будет допущена ошибка, дисперсия которой равна:

s²_{e =}

Если же рассматриваемый сигнал X(t) заменить последовательностью дискретных значений, взятых через интервал 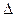t=1/(2F) , то дисперсия ошибки восстановления исходного непрерывного сигнала по этим значениям будет больше, чем s_e² по следующим причинам (см. рисунок 4):

0 f

Рисунок 4

Точное выделение спектра исходного сигнала невозможно. Наиболее целесообразно выбрать характеристику фильтра, как показано на рисунке 3. Ошибки, воспроизведенного непрерывного сигнала, таким образом, обусловлены наличием отброшенных “хвостов” основного спектра s_e², и S_x(f) площадью частей кратных спектров, попадающих в полосу фильтра.

Один из подходов к решению задачи:

Пропустим сигнал через НЧ фильтр с полосой пропускания F. Получим сигнал с ограниченным спектром S₀(f).

S₀ (f)

F

-F

f

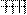Рисунок 5

Этот сигнал X₀(t ) отличается от исходного X(t) , отличие можно характеризовать ошибкой s_e²:

s_e²=M[X(t)-X₀(t)]²

Эта ошибка равна заштрихованной площади на рисунке 5

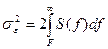
Зная S(f) ошибку легко вычислить. Полученный сигнал удовлетворяет условиям теоремы Котельникова. Выбрав 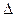t=1/(2F) , можно точно воспроизвести сигнал X₀(t) , а сигнал X(t) с ошибкой s_e².

Если задано допустимое значение s_e² , то F можно выбрать из условия:

1.4 Критерий Железнова

Дальнейшее развитие теория квантования по времени случайных процессов получила в работах Н.А. Железнова. Модель сигнала по критерию Железнова, следующая:

- сигнал представляет собой случайный квазистационарный процесс;

- сигнал ограничен по времени интервалом времени T_c;

- спектр сигнала сплошной и бесконечный;

- интервал корреляции t₀ << T_c;

- мгновенная мощность сигнала ограничена и не может меняться скачком.

Критерий Железнова:

Квазистационарный сигнал с неограниченным спектром определяется со сколь угодно малой ошибкой последовательностью своих дискретных значений, следующих друг за другом через интервалы 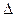t, если 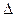t £ t₀.

Ряд Железнова имеет вид:

,

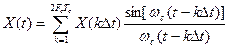где F_c=1/(2 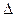t); w_c=2pF_c.

Существенным преимуществом критерия Железнова является приближение модели сигнала к реальным условиям (неограниченность спектра и конечная длительность сигнала).

1.5 Критерий аппроксимации

В тех случаях, когда закон изменения функции с определенной достоверностью известен, более целесообразным является метод, основанный на замене непрерывной исходной функции аппроксимирующей функцией.

Также метод аппроксимации применим в случае, когда возникает трудность практической реализации методов Котельникова и Железнова.

Простейшим видом аппроксимации является аппроксимация полиномом первого порядка, при этом производится кусочно-линейная аппроксимация кривой функции, т. е. все точки кривой исходной функции, соответствующие отсчетным моментам времени, соединяются отрезками прямых.

dmax

X(t)

…

ti

t2

ti+1

t1

t

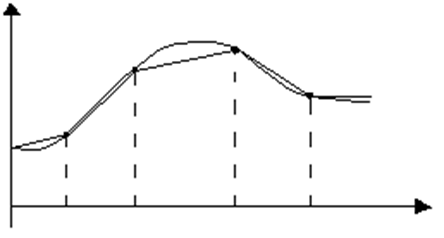
Рисунок 6

Выбор частоты квантования производится по критерию отклонения аппроксимирующей функции от исходной на каждом из интервалов дискретизации 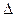t_i .

Для этих целей применяются такие критерии, как критерий наибольшего отклонения, среднеквадратичный интегральный и вероятностный. В первом случае необходимая частота квантования выбирается из условия, чтобы предельные отклонения аппроксимирующей ломаной прямой от действительного значения функции (рис. 6) не превосходили бы заданного значения. Задача может быть решена с помощью интерполяционной формулы Ньютона, в соответствии с которой значение функции для любого момента времени внутри интервала 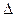t=t_i+1-t_i определяется выражением X^’(t)=X(t_i)+a_i(t-t_i)a_i=[X(t_i+1)-X(t_i)]/(t_i+1-t), где погрешность аппроксимации определяется остаточным членом интерполяционной формулы |d|=|l(t)|=X’(t)-X(t).

В рассматриваемом случае остаточный член выражается следующим образом:

l(t)= 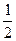(t-t_i)(t-t_i+1)d²X(t)/dt²

Очевидно, что max значение погрешности аппроксимации

|s|_max=|l(t)|_max=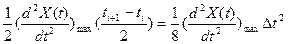

Следовательно, задаваясь допустимой погрешностью аппроксимации s_max , можно определить интервал и частоту квантования.

,

Метод аппроксимации полиномом страдает определенной неточностью, обусловленной тем, что точный закон изменения функции X(t) практически не известен, и поэтому невозможно точно определить max значение второй производной функции.

Более высокую точность обеспечивает аппроксимация полиномом, имеющим порядок выше первого.

2 Методика выполнения работы

1. По аналитически заданной функции X(t) определить её спектр и найти max частоту F_c .

2. Найти интервал дискретизации Dt_k по теореме Котельникова.

3. Для удобства дальнейших действий перейти к относительному времени . При использовании переменной z запись ряда Котельникова упрощается и принимает вид:

Записать функцию X(t), заменив переменную на 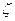, для этого выполнить следующее:

3.1. Заменить в преобразованном выражении функции Х(t) круговую частоту w на линейную F.

3.2. Выразить F_c через Dt в соответствии с теоремой Котельникова и подставить в формулу для Х(t).

3.3. Произвести окончательную замену переменной 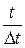на z.

4. Определить значения функции Х(t) в точках отсчета, кратных Dt. Для переменной z это эквивалентно расчету значений функции Х(z) при z = 1, 2, 3…10. Результаты занести в таблицу 1.

Таблица 1

z				…
Х(z)

5. Исследовать поведение истинной и восстановленной функций X( 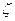) и X_восст( 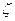) на интервале между пятым и шестым отсчетами 5£ 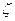£6 с шагом D 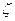=0,125.

Для этого:

5.1. Рассчитать по программе , приведенной в приложении, значения функции, восстановленной с помощью ряда Котельникова: X_восст(5), X_восст(5,125)…… X_восст(5,875), X_восст(6)

Результаты занести в таблицу 2.

5.2. Рассчитать по аналитическому выражению функции X( 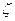) истинные значения в тех же точках: X(5), X(5,125)…… X(5,875), X(6) и занести в таблицу 2.

Таблица 2

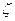	5,0	5,125	5,250	5,375	5,5	5,625	5,75	5,875	6,0
Хист( )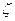
Хвосст( )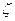
e

6. Определить математическое ожидание m_e и среднеквадратическое значения d_e ошибки восстановления e по формулам:

,

,

.

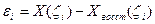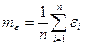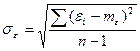Заключение

В информационных системах передача непрерывных сигналов осуществляется с помощью их дискретных значений, взятых в отдельные моменты времени. При этом возникает целый круг задач, связанных с точностью восстановления непрерывного сигнала по дискретным значениям и выбором интервала дискретизации, а также с оценками потерь информации при замене непрерывного сигнала дискретным и с вопросами кодирования дискретного сигнала и избыточности.

При проектировании систем с требуемой точностью первоочередной задачей является определение интервала дискретизации, при котором ошибка восстановления исходного сигнала не должна превышать заданного значения. При этом достаточно найти соотношения, связывающие величину интервала дискретизации с ошибкой восстановления исходного сигнала. Из этих соотношений при заданной точности может быть определена величина интервала или частота дискретизации.

Чтобы получить зависимость ошибки интервала дискретизации, необходимо знать свойства сигнала, подлежащего дискретизации, которые могут быть заданы в виде различных характеристик и ограничений. В частности, это могут быть спектральные характеристики, ограничения на величину сигнала и его производные. В зависимости от конкретных условий применяют различные методы решения постановленной задачи. Может быть рассмотрена задача дискретизации сигналов с ограниченным спектром при отсутствии помех, дискретизации сигналов с неограниченным спектром при отсутствии помех, дискретизации непрерывных сигналов при наличии помех.

Задача дискретизации имеет три основных аспекта - это выбор интервала дискретизации, разработка методики восстановления непрерывного сигнала по дискретным значениям и оценка ошибки восстановления.

Приложение А

Программа вычисления ряда Котельникова:

F p	´	П Д	О	ИП О	ИП Д	ПП		ИП 1	ПП
	ИП 2	ПП		ИП 3	ПП		ИП 4	ПП
ИП 5	ПП		ИП 6	ПП		ИП 7	ПП		ИП 8
ПП		ИП 9	ПП		ИП А	ПП		ИП В	ПП
	ИП С	ПП		С/П	БП	ОО	ИП Д	F p	-
П Д	F sin	ИП Д	¸	´	+	В/О

Инструкция:

1. Установить переключатель Р-Г в положение Р

2. Перейти в программируемый режим, нажав клавиши F и ПРГ и ввести текст программы.

3. Вернутся в режим автоматического счета нажав клавиши F и АВТ

4. Ввести исходные данные в память: Х₀® П0

Х₁®П1

----------

Х₉®П9

Х₁₀®ПА

5. Ввести текущее значение 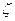в регистр Х, т.е. набрать на клавиатуре.

6. Нажать клавиши В/О и С/П.

7. По окончании счета //время счета около 70 сек.// считать значение Х( )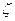

Тест:

При исходных данных:

Х₀=5

Х₁=6

Х₃=8

Х₄ =9

Х₂=7

Х₅=10

Х₆=0

Х₇=1

Х₈=2

Х₉=3

Х₁₀=4

И 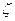=5,5

должен получиться результат:

Х( 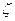)=5,0259

Затем записать в ячейки памяти свои исходные данные из таблицы 1 и рассчитать восстановленные значения функции Х( 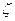), повторив пункты 3-5 для следующих значений 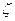=5; 5.125; … 5.875; 6, полученные значения записать в таблицу 2.

Список литературы

1. И.В. Кузьмин, В.А. Кедрус “Основы теории информации и кодирования”. Киев, 1977г.

2. А.К. Трохименко, Ф.Д. Любич “Радиотехнические расчеты на микрокалькуляторах” . 1983г.