Задания для самостоятельной работы 1 страница

МОЛЕКУЛЯРНАЯ ФИЗИКА И

ТЕРМОДИНАМИКА

СБОРНИК

ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ФИЗИКЕ

Новосибирск 2016

УДК: 53(075)

Составители: доц. И.М. Дзю, д.т.н., проф. С.В. Викулов, ст. преп. А.П. Минаев

Рецензент: к.т.н., доц., Е.П. Матус, НГАСУ (Сибстрин)

Молекулярная физика и термодинамика. Сборник индивидуальных заданий по физике / Новосиб.гос.аграр.ун-т. Инженерный ин-т; сост.:И.М. Дзю, С.В. Викулов, А.П. Минаев – Новосибирск: НГАУ, 2016. – 84 с.

Сборник индивидуальных заданий по физике (Молекулярная физика и термодинамика): составлен в соответствии с действующей программой курса физики. Каждое индивидуальное задание содержит 11 задач, охватывающие основные понятия молекулярной физики и термодинамики.

Предназначенно для студентов обучающихся по всем направлениям и формам обучения, реализуемым в НГАУ.

Утверждено и рекомендовано к изданию методическим советом Инженерного института протокол №7 от 1 марта 2016 г.

@ Новосибирский ГАУ,2016

ВВЕДЕНИЕ

В учебном пособии рассмотрены три темы: «Молекулярная физика», «Основы термодинамики» и «Реальные газы и жидкости».Материал тем изложен следующим образом. Кратко изложена суть рассматриваемых тем, по каждой из них в систематизированной форме приведены основные законы и формулы. Приведены примеры решения типовых задач и двенадцать вариантов индивидуальных заданий.

Пособие может быть использовано на практических и контрольных занятиях, при выполнении домашних заданий, а также при самостоятельном изучении курса физики.

МОЛЕКУЛЯРНАЯ ФИЗИКА

Молекулярная физика – раздел физики, изучающий строение и свойства вещества исходя из молекулярно – кинетических представлений, основы­вающихся на том, что все тела состоят из атомов и молекул, находящих­ся в непрерывном хаотическом движении. Атомы и молекулы взаимодействуют между собой с силами притяжения и отталкивания.

Законы поведения огромного числа моле­кул, являясь статистическими закономер­ностями, изучаются с помощью статисти­ческого метода.

Агрегатные состояния вещества: 1) твёрдое тело; 2) жидкость; 3) газ; 4) плазма.

Модель идеального газа:1) собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда; 2) между молекулами газа отсутствуют силы взаимодействия; 3) столкновения молекул газа между собой и со стенками сосуда абсолютно упругие.

Основные законы и формулы

Количество вещества одно­родного газа (моль)

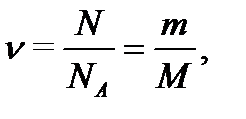(1.1)

где N- число молекул газа; 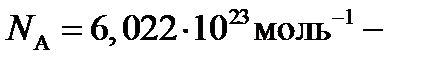число Авогадро; 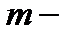масса газа, кг; 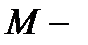молярная масса, кг/моль; M- молярная масса.

Количество вещества смеси газов

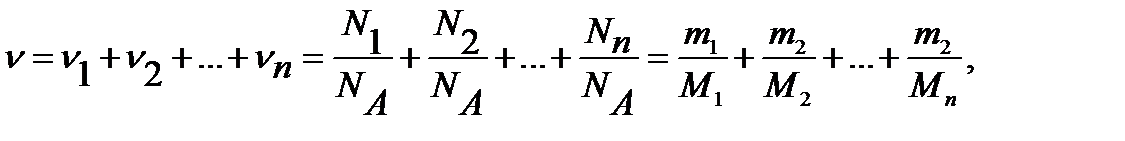(1.2)

где 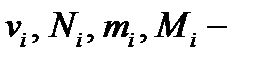соответственно количество вещества, число молекул, масса, молярная масса i - й компоненты смеси.

Уравнение Клапейрона – Менделеева

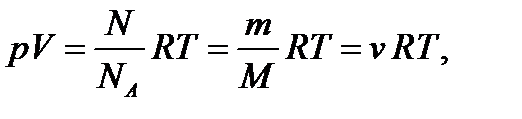(1.3)

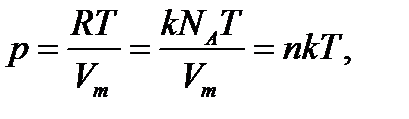(1.4)

где 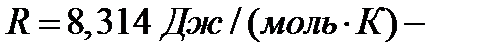универсальная газовая постоянная; 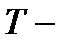термодинамическая температура, К; 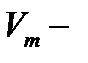молярный объём, м³/моль; 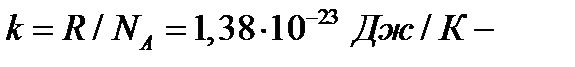постоянная Больцмана; 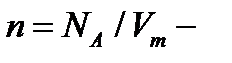концентрация молекул (число молекул в единице объема).

Число Лошмидта – число молекул, содержащихся в 1 м³ газа при нормальных условиях ( 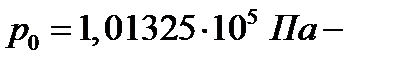давление; 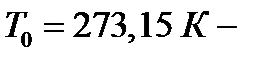термодинамическая температура)

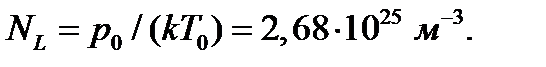(1.5)

Основное уравнение молеку­лярно - кинетической тео­рии газов

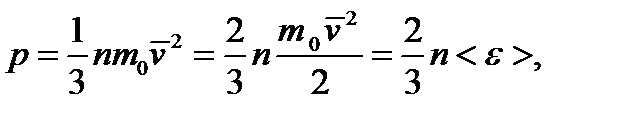(1.6)

где 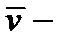средняя квадратичная скорость, м/с; 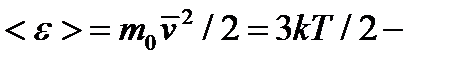средняя кинетическая энергия молекулы газа.

Распределение молекул идеального газа по скоростям (закон Максвелла)

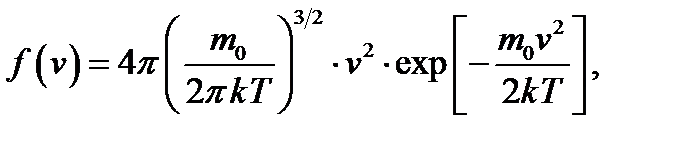
где 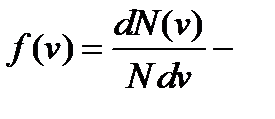функция распределения, которая определяет относительное число молекул 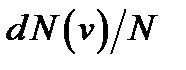, скорости которых лежат в диапазоне от 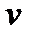до .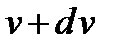

Функция 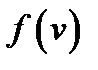удовлетворяет условию нормировки

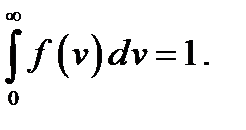
Характерные скорости функции распределения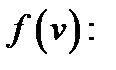

1) наиболее вероятная

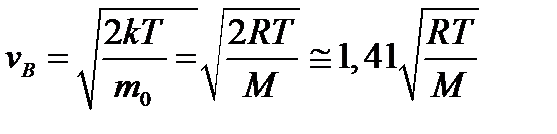, (1.7)

2) средняя арифметическая

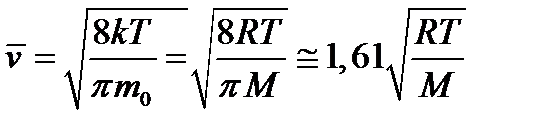, (1.8)

3) средняя квадратичная

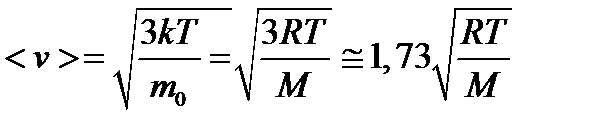. (1.9)

Распределение молекул идеального газа по энергиям теплового движения

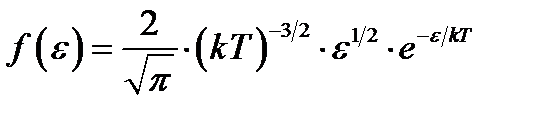. (1.10)

Средняя кинетическая энергия 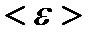молекулы идеального газа

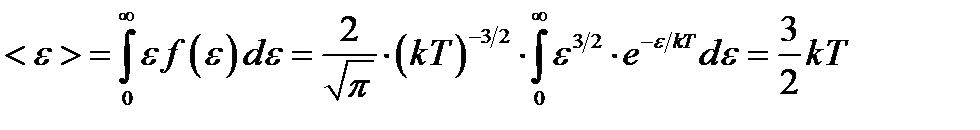. (1.11)

Барометрическая формула

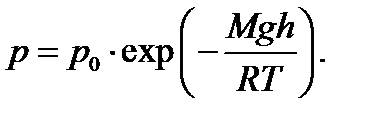(1.12)

Распределение Больцмана

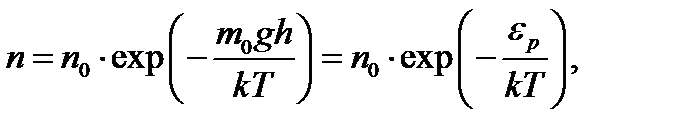(1.13)

где 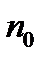- концентрация молекул в том месте, для которого 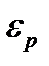принята равной нулю, 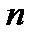- концентрация молекул в том месте, где потенциальная энергия молекулы равна .

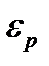Средняя длина свободного пробега молекул

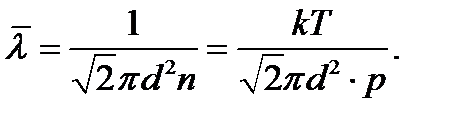(1.14)

Среднее число столкновений молекулы за 1 с

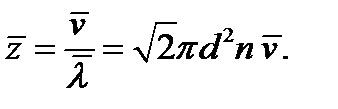(1.15)

Закон диффузии Фика

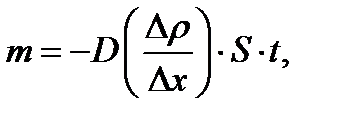(1.16)

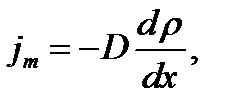(1.17)

где 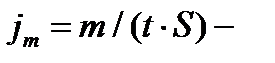плотность потока массы – величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х; 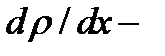градиент плотности; 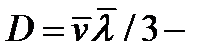коэффициент диффузии.

Закон теплопроводности Фурье

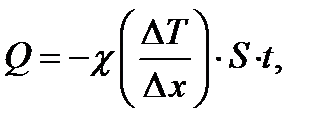(1.18)

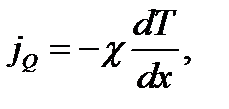(1.19)

где 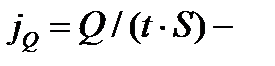плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х; 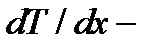градиент температуры; 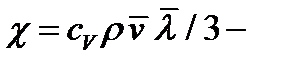коэффициент диффузии, где 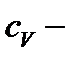удельная теплоёмкость газа при постоянном объёме.

Закон внутреннего трения (вязкости) Ньютона

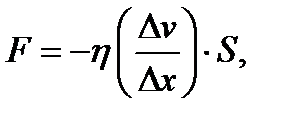(1.20)

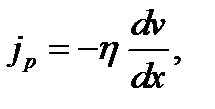(1.21)

где 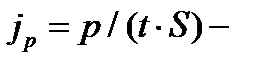плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси х через единичную площадку, перпендикулярную оси х; 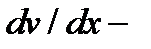градиент скорости; 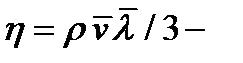коэффициент внутреннего трения (динамическая вязкость).

ОСНОВЫ ТЕРМОДИНАМИКИ

Термодинамика –раздел физики, изу­чающий общие свойства макроскопиче­ских систем, находящихся в состоянии термодинамического равновесия, и про­цессы перехода между этими состояниями. Термодинамика не рассматривает микро­процессы, которые лежат в основе этих превращений. Этим термодинамический методотличается от статистического метода. Термодинамика базируется на двух на­чалах – фундаментальных законах, уста­новленных в результате обобщения опыт­ных данных.

Молекулярно-кинетическая теория и термодинамика взаимно дополняют друг друга, образуя единое целое, но отличаясь различными методами исследования. Термодинамика имеет дело с термоди­намической системой– совокупностью макроскопических тел, которые взаимо­действуют и обмениваются энергией, как между собой, так и с другими телами (внешней средой).

Основные законы и формулы

Средняя энергия молекулы

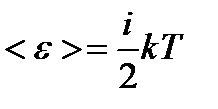, (2.1)

где i – сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы:

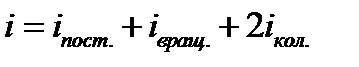. (2.2)

Внутренняя энергия для произвольной массы т газа

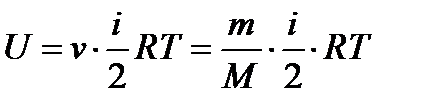. (2.3)

Первое начало термодинамики

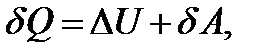(2.4)

т.е. количество тепла, сообщённое системе, идёт на приращение внутренней энергии системы и на совершение системой работы над внешними телами.

Молярная теплоёмкость при постоянном объёме

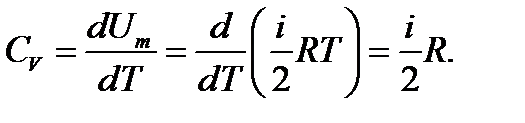(2.5)

Молярная теплоёмкость при постоянном давлении (уравнение Майера)

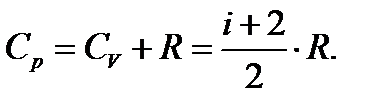(2.6)

Отношение теплоёмкостей 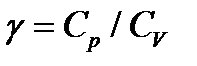(показатель адиабаты)

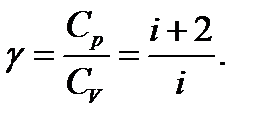(2.7)

Работа газа при изменении его объёма от 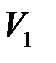до

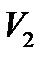
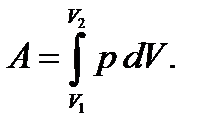(2.8)

Работа газа при изобарном расширении

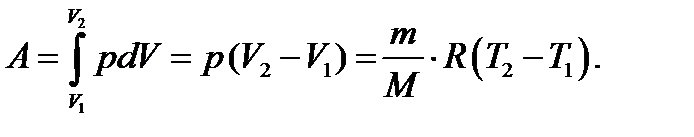(2.9)

Работа газа при изотермическом расширении

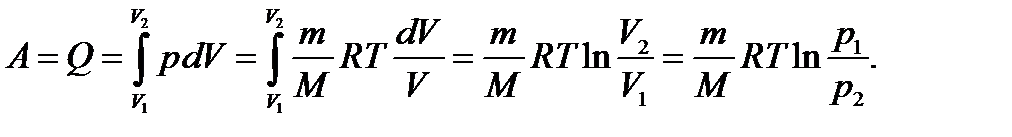(2.10)

Уравнения адиабатического процесса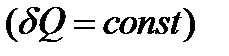

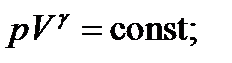
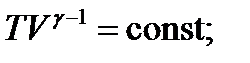
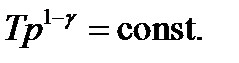(2.11)

Работа газа при адиабатическом расширении

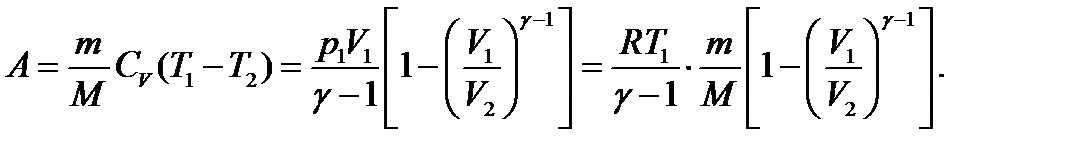(2.12)

Термический коэффициент полезного действия для кругового процесса

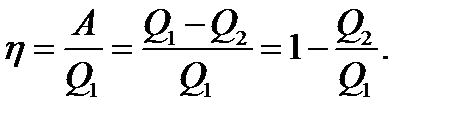(2.13)

Термический коэффициент полезного действия цикла Карно

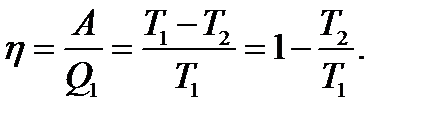(2.14)

Второе начало термодинамики

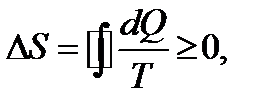(2.15)

т.е. энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).

Изменение энтропии в процессах идеального газа

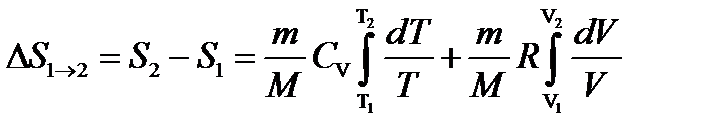
или 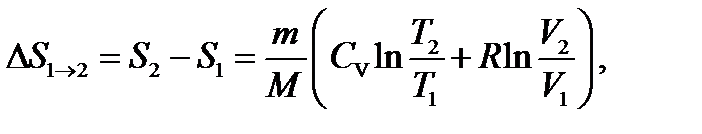(2.16)

т.е. изменение энтропии 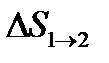идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода 1 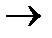2.

РЕАЛЬНЫЕ ГАЗЫ И ЖИДКОСТИ

Критерием различных агрегатных состояний вещества является соотношение между величинами наименьшей потенциальной энергии взаимодействия молекул 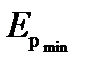и тепловой энергии 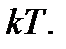Наименьшая потенциальная энергия взаимодействия молекул 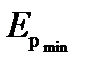определяет работу, которую нужно совершить против сил притяжения для того, чтобы разъединить молекулы, находящиеся в равновесии ( 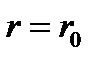); 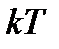определяет удвоенную среднюю энергию, приходящуюся на одну степень свободы хаотического движения молекул.

Если 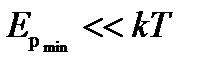, то вещество находится в газообразном состоянии, так как интенсивное тепловое движение молекул препятствует соединению молекул, сблизившихся до расстояния 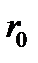, т.е. вероятность образования агрегатов из молекул достаточно мала.

Если 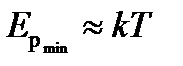, то вещество находится в жидком состоянии, так как в результате теплового движения молекулы перемещаются в пространстве, обмениваясь местами, но не расходясь на расстояние, превышающие .

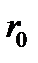Если 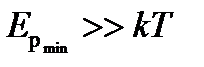, то вещество находится в твёрдом состоянии, так как молекулы, притягиваясь друг к другу, не могут удалиться на значительные расстояния и колеблются около положений равновесия, определяемого расстоянием .

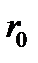Таким образом, любое вещество в зависимости от температуры может находиться в газообразном, жидком или твёрдом агрегатном состоянии, причём температура перехода из одного агрегатного состояния в другое зависит от значения 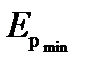для данного вещества. Например, у инертных газов 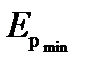мало, а у металлов велико, поэтому при обычных (комнатных) температурах они находятся соответственно в газообразном и твёрдом состояниях.

Основные законы и формулы

Уравнение Ван-дер-Ваальса для моля реального газа

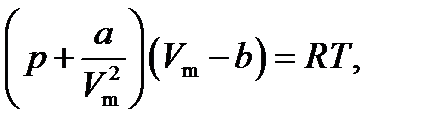(3.1)

где р – давление, оказываемое на газ извне (равное давлению газа на стенки сосуда), а и b – постоянные Ван-дер-Ваальса, имеющие для разных газов различные значения, определяемые экспериментально.

Уравнение Ван-дер-Ваальса для произвольного количества газа

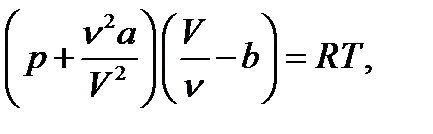(3.2)

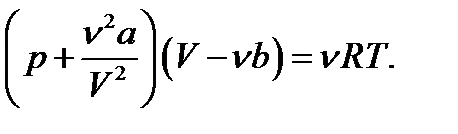или (3.3)

Критические параметры изотермы Ван-дер-Ваальса

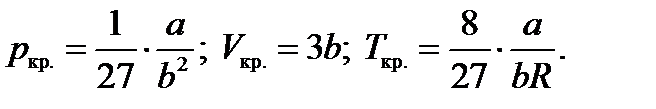(3.4)

Количество теплоты, необходимое для нагревания тела в твердом или жидком состоянии в пределах одного агрегатного состояния

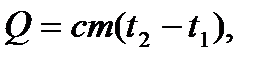(3.5)

где 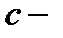удельная теплоемкость тела, 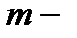масса тела, 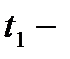начальная температура, 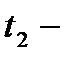конечная температура.

Количество теплоты, необходимое для плавления твёрдого тела

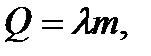(3.6)

где 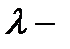удельная теплота плавления, 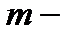масса тела.

Количество теплоты, необходимое для испарения

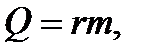(3.7)

где 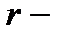удельная теплота парообразования, 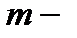масса тела.

Коэффициент поверхностного натяжения жидкости

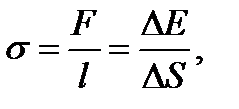(3.8)

где F − сила поверхностного натяжения, действующая на контур, ограничивающий поверхность жидкости; 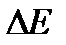− изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади 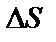поверхности этой пленки.

Формула Лапласа для сферической поверхности жидкости

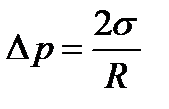, (3.9)

где R − радиус сферической поверхности.

Формула Лапласа для цилиндрической поверхности жидкости

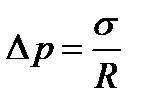, (3.10)

где R − радиус цилиндрической поверхности.

Высота подъема жидкости в капиллярной трубке (формула Жюрена)

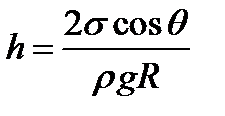, (3.11)

где 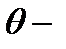краевой угол; R − радиус канала трубки; 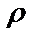− плотность жидкости; g − ускорение свободного падения.

Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями

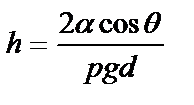, (3.12)

где d – расстояние между плоскостями.

УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ

При решении задач необходимо выполнять следующее:

1. Записать столбиком данные задачи. Все величины выразить в единицах системы СИ. Выполнить чертеж или рисунок, поясняющий содержание задачи. Записать основные формулы, на которых базируется решение, дать словесную формулировку этих законов, разъяснить буквенные обозначения формул. В случае, если формула не выражает какой-нибудь физической величины, ее надо вывести.

2. Решение задачи сопровождать краткими, но исчерпывающими пояснениями.

3. Решать задачу необходимо в общем виде, т.е. от начала и до конца решение выполняется в буквенном виде, числовые значения подставляются в окончательную рабочую формулу, выражающую искомую величину.

4. Подставить в рабочую формулу размерности величин и убедиться в правильности размерности искомой величины или ее единицы.

5. Произвести вычисление величин, подставленных в формулу, руководствуясь правилами приближения вычислений, записать в ответе числовое значение и сокращенное наименование единицы искомой величины по ГОСТу.

6. При подготовке в рабочую формулу, а также при записи ответа числовые значения величин записать как произведение десятичной дроби с одной значащей цифрой перед запятой на соответствующую степень десяти.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

ВАРИАНТ 1

1. Пустой баллон заполнен газом при температуре 278 К, создано давление 8 атм и закачано 10 кг газа. Затем баллон внесли в помещение, где температура равна 20°С. В результате использования газа его давление понизилось на 300 кПа и при этом температура газа не изменилась. Сколько газа было взято? [Ответ 3,56 кг]

2. В закрытом сосуде емкостью 2 м³ находятся 1,4 кг азота и 2 кг кислорода. Найти давление газовой смеси в сосуде, если температура смеси 27°С.

[Ответ:140 кПа]

3. Температура одноатомного газа равна 37°С, а объём 3 л. Определить концентрацию молекул газа и его давление, если внутренняя энергия газа равна 340 Дж. [Ответ:75,6 кПа; 1,77·10²⁵ м³]

4. Во сколько раз изменится средняя скорость движения молекул двухатомного идеального газа при адиабатном увеличении давления в два раза.

[Ответ: 0,82]

5. Между двумя пластинами, находящимися на расстоянии 1 мм друг от друга, находится воздух. Между пластинами поддерживается разность температур 1°С. Площадь каждой пластины 100 см² . Какое количество тепла передается за счет теплопроводности от одной пластины к другой за 10 мин? Считать, что воздух находится при нормальных условиях. Диаметр молекулы воздуха 3·10^-10м. [Ответ: 77,3 Дж]

6. Некоторый газ при нормальных физических условиях имеет плотность 0,0894 кг/м³ . Определить его удельные теплоемкости С_р и С_v, а также какой это газ. [Ответ: 14,56 10³ Дж/кг·К; 10³ Дж/кг·К ]

7. Воздух, находящийся под давлением 1 атм, был адиабатически сжат до давления 10 атм. Каково будет давление сжатого воздуха, если его охладить до первоначальных параметров, сохранив неизменным объём?

[Ответ:0,519 МПа]

8. Работа изотермического расширения 5 г некоторого газа от объёма V до объёма 3V равна 800 Дж. Найти среднюю квадратичную скорость молекул газа при этих условиях. [Ответ: 660 м/с]

9. 2 кмоля многоатомного газа нагреваются на 80°С в условиях свободного газу, изменение его внутренней энергии, работу расширения.

[Ответ: 5,3 МДж; 4 МДж; 1,3 МДж]

10. Тепловая машина, работающая по циклу, диаграмма которого изображена на данном рисунке, включает изохорный, изобарный и изотермный процессы и имеет следующие параметры: Р₁=2,5 атм, V₁=1,5 л, Р₂=16,6 л. Вычислить к.п.д. цикла, если в работе задействован двухатомный газ; кпд цикла Карно с данными температурами. [Ответ: 19%85%]

11. Разность уровней жидкости в коленах U-образной трубки равна 23 мм. Диаметры каналов в коленах трубки равны 2 и 0,4 мм. Плотность жидкости 800 кг/м³ . Определить коэффициент поверхностного натяжения жидкости.

[Ответ: 0,045 Н/м]

ВАРИАНТ 2

1.Один баллон емкостью 20 л содержит газ при давлении 25 атм, другой баллон емкостью 44 л содержит тот же газ при давлении 16 атм. Оба баллона были соединены вместе, образовалась однородная смесь (Т=const). Найти парциальные давления обоих газов и полное давление.

[Ответ: 7,8 атм; 5 атм; 12,8 атм]

2. Давление воздуха в автомобильной камере при температуре -13°С было 160 кПа (избыточное над атмосферным). Каким стало давление, если в результате длительного движения воздух в камере нагрелся до 37°С?

[Ответ: 210 кПа (сверх атмосферного)]

3. Средние квадратичные скорости и концентрация молекул идеального газа в двух сосудах одинаковы. Масса газа во втором сосуде в три раза меньше, чем в первом. Чему равно отношение давлений в сосудах? [Ответ: 3]

4. Колба вместимостью 4 л содержит некоторый газ массой 0,62 г под давлением 200 кПа. Определить среднюю квадратичную скорость молекул газа. [Ответ: 1967 м/с]

5. Расстояние между стенками сосуда Дьюара равно 10^-2м. При каком давлении теплопроводность воздуха, находящегося между стенками сосуда, начнет уменьшаться при откачке? Температура воздуха 27°С, диаметр молекулы принять равным 3·10^-10м. [Ответ: 1,05 Па]

6. Плотность газа при нормальных условиях равна 1,25 кг/м³ , отношение удельных теплоемкостей 1,4. Определить удельные теплоемкости при постоянном давлении и постоянном объеме.

[Ответ: 1025,6 Дж/кг·К; 732,6 Дж/кг·К]

7. Определить работу адиабатного расширения водорода, масса которого 4 г, если температура газа понизилась на 10°С. [Ответ: 416 Дж]