Нерівноважні термодинамічні функції

Лекція 2. Теорія Онзагера. Сили в термодинаміці необоротних процесів. Потоки. Теорема Онзагера. Приріст ентропії

Теорія Онзагера

Ми вже згадували, що необоротне явище може виникнути з ряду причин. Цими причинами можуть бути температурний градієнт, градієнт концентрації, градієнт потенціалу, хімічна спорідненість і ін. У термодинаміки необоротних процесів всі вони носять назву сил і позначаються через Х_i (i = 1, 2, ..., n). Ця назва може ввести в оману, оскільки ці сили нічого спільного не мають з силами в ньютонівському розумінні цього терміна. Назва «спорідненість» (affinity), застосовуване деякими авторами, більш переважно для цього поняття. Ми бачили, що сили викликають відомі необоротні явища, як, наприклад, потік тепла, дифузійний потік, електричний струм і хімічні реакції. Всі вони називаються потоками (fluxes) і позначаються через J_i (i -1, 2, ..., n).

У найбільш загальному випадку будь-яка сила може викликати будь-який потік. Так, градієнт концентрації, так само як і градієнт температури, може викликати потік дифузії (звичайна дифузія і термодифузія). Обидві ці сили можуть також викликати тепловий потік (ефект Дюфора і теплопровідність). Ця обставина дозволяє описати будь яке необоротне явище в загальному вигляді наступним феноменологічним співвідношенням:

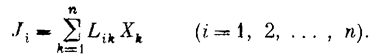(1)

Воно встановлює, що будь-який потік виникає під дією всіх сил. Коефіцієнти L_ik (i = 1, 2, ..., n) називаються феноменологічними коефіцієнтами. Коефіцієнти L_ii - це, наприклад, теплопровідність, коефіцієнт звичайної дифузії, електропровідність, коефіцієнт хімічної спорідненості. Коефіцієнти L_ik при i ≠k пов'язані з явищами, що накладаються. Прикладами є коефіцієнт термодифузії, коефіцієнт Дюфора і т. д.

Тепер можна сформулювати основне положення, на якому базується справжня монографія.

Теорема Онзагера встановлює, що при відповідному виборі потоків J_i і сил Х_i матриця феноменологічних коефіцієнтів має бути симетричною тобто

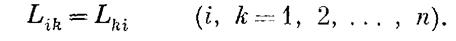(2)

Ці тотожності називаються співвідношеннями Онзагера. Вони встановлюють зв'язок між двома накладаються явищами (як, наприклад, термодифузію і ефектом Дюфора). Цей зв'язок виникає від взаємного накладення необоротних процесів, що протікають одночасно (у наведеному прикладі - теплопровідність і потік дифузії).

Тепер слід встановити, що розуміється під терміном «відповідний вибір» потоків і сил. Для цієї мети уявімо собі адіабатично ізольовану систему. Припустимо, що стан системи характеризується відомими параметрами A₁, A₂, ..., А_n (як, наприклад, тиск, температура, концентрація і т. д.). Позначимо значення цих параметрів у стані термостатичної рівноваги через A⁰₁, A⁰₂, ...., A⁰_n. Для зручності будемо користуватися змінами цих параметрів стану від їх значень при рівновазі α_i = A_i - A⁰_i з відповідними значками i = 1, 2, ..., n. У стані рівноваги ентропія має максимальне значення, а значення всіх змінних параметрів α_i дорівнюють нулю. Це означає, що для нерівноважного стану зміну ентропії DS від її значення при рівновазі можна в першому наближенні написати у вигляді співвідношення

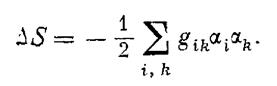(3)

Тепер є можливість дати визначення потокам і силам, які входять у вираз (1). Ці потоки і сили в онзагеровском розумінні являють собою похідні за часом параметрів стану a_i:

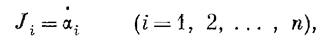(4)

а силами є наступні функції параметрів стану:

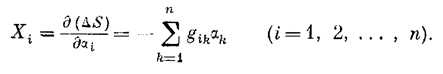(5)

У цьому полягає основний зміст (сенс) теореми Онзагера.

Велике значення має похідна ентропії за часом. Її називають «виникненням ентропії». Вона дає величину збільшення ентропії у незворотному процесі за одиницю часу

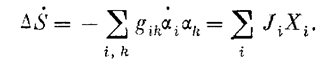(6)

Цим виразом користуються для вибору - потоків J_i і сил Х_i, коли відомо DS. Потоки J_i і сили Х_i з однаковими значеннями i називаються сполученими (сопряженными) параметрами. Слід зазначити, що при виборі потоків і сил є деяка свобода тому, що вираз для DS може бути різним шляхом розчленоване на суму сполучених J_i і X_i. Однак, у всіх випадках співвідношення Онзагера (2) залишаються в силі.

Резюмуючи викладене, можна сказати, що термодинамічна теорія J_i і Х_i з рівняння (6) шляхом визначення, а потім використанні рівняння (1) і співвідношень взаємності Онзагера (2). Ця теорія, незважаючи на свою простоту, виявляється справедливою для будь-якого процесу. Тому назва «Термодинаміка незворотних процесів» є цілком виправданою для цієї галузі знань.

Дотепер ми ще нічого не говорили про доведенні теореми Онзагера. Хоча цей параграф призначений головним чином для того, щоб сформулювати основні висновки досліджень Онзагера (математичне доказ цих положень дається у другому розділі), ми відзначимо тут деякі особливості цього докази. Теорема Онзагера доводиться загальними методами статистичної механіки. Співвідношення взаємності Онзагера (2) доводяться шляхом використання властивостей мікроскопічної оборотності, тобто, симетрії всіх рівнянь руху окремих частинок по відношенню до часу, або, іншими словами, інваріантності переходу t ® -t. Це справедливо як для класичної механіки, так і для квантової. Онзагеровске рішення не вимагає будь-яких деталей, що характеризують даний конкретний рух. Це означає, що результат є загальним і справедливим для будь-якого незворотного процесу. Теорема Онзагера, базуючись на мікроскопічному стані фізичної системи, дає висновки, справедливі з макроскопічної точки зору. Точно так само йде справа з другим законом термодинаміки.

Цікаво відзначити, що Оізагер розробив свою теорію шляхом розгляду двох спеціальних випадків: теплопровідності анізотропного кристалу і потрійний молекулярної хімічної реакції. Перший є очевидною ілюстрацією співвідношень (2), а другий показує зв'язок співвідношень (2) з мікроскопічної оборотністю.

Коли на систему впливає зовнішнє магнітне поле В, співвідношення Онзагера (2) приймають вигляд

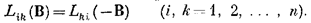(7)

Це означає, що коефіцієнт L_ikє така ж функція В, як L_ki є функція -В. Це має фізичний зміст навіть для випадку, коли i = k, показуючи, що перехресні елементи матриці Lik є також функціями напруженості магнітного поля. Вихідним для співвідношення (7) є спеціальна форма вираження лоренцової сили. Вона, будучи векторним добутком швидкості частинки і магнітного поля, має певний вплив на мікроскопічну оборотність. Це означає, що потрібно не тільки змінити швидкість, але також і подолати магнітне поле, щоб всі часточки повернути на колишній шлях.

Нерівноважні термодинамічні функції

Ми згадували, що для знаходження сполучених потоків J_i і сил X_i потрібно підрахувати виникнення ентропії DŚ, яке вийшло в результаті процесу. Існує два звичайних способу підрахунку виразу (6). У першому з них визначається зміна ентропії в адіабатично ізольованої системі по рівності (3), після чого знаходиться виникнення ентропії по рівнянню (6). У другому способі з рівняння балансу ентропії для макросистеми знаходиться вираз виникнення ентропії. Виходячи з особливостей конкретного завдання, встановлюється, який з двох методів зручніше використовувати в тому чи іншому випадку. В обох випадках доводиться користуватися законом збереження маси, енергії, кількості руху і другим законом термодинаміки у формі рівності.

Характерно, що ця частина теорії необоротних процесів була розроблена значно раніше теорії Онзагера. Цінні роботи з цього питання були опубліковані Дюгемом, Натансоном, Яманом, Лором і дe Донде.

Для того щоб сформулювати найважливіші положення цієї теорії, можна написати вираз зміни ентропії системи за відомий проміжок часу по Карно - Клаузиусу

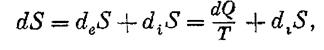(8)

де: d_eS і dQ - відповідно ентропія і тепло, повідомлені системі з навколишнього середовища, d_tS - ентропія, що виникла всередині системи в результаті незворотного процесу за той же проміжок часу.

Тут передбачається, що система є закритою, тобто має місце тільки теплообмін з навколишнім середовищем, а обмін масою відсутній. Якщо система обмінюється з навколишнім середовищем масою, то така система називається відкритою і d_eS включає додатковий член, що характеризує отримання системою ентропії за рахунок обміну масою. Зовнішнє зміна ентропії d_eS може бути позитивною, негативною, а також мати значення, рівне нулю, у той час як внутрішня зміна ентропії d_iS, безумовно, завжди позитивна. Відзначимо, що Клаузіус користувався позначенням dQ'замість Td_iS і називав цю величину не зовсім вдало «некомпенсованим теплом».

За допомогою наведеного формулювання основного виразу термодинаміки незворотних процесів (8) дуже легко показати, які випадки розглядаються звичайної термодинамікою (термостатикою). Можливий один з наступних двох випадків:

1) d_iS = 0, тоді другий закон дає для оборотних процесів

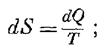(9)

2) d_iS> 0. Цей випадок призводить до того, що

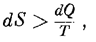(10)

і відноситься до незворотних процесів.

У термодинаміки необоротних процесів користуються виразом (8), для того щоб можна було підрахувати внутрішня зміна ентропії d_iS, що виникло в дійсному(справжньому) процесі. Деякі прості приклади такого підрахунку наведені в літературі у зв'язку з теплопровідністю і в у зв'язку з хімічними реакціями. Цей підрахунок грунтується на двох гіпотезах. Одна з них полягає в тому, що зміна ентропії завжди позитивна, а інша є рівнянням Гіббса

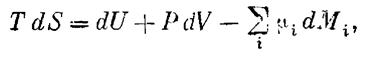(11)

де U - енергія, V - об'єм, Р - тиск, М - маса, m_i - хімічний потенціал i компонента системи. Дана залежність ґрунтується на термостатичній рівновазі з навколишнім середовищем, при цьому приймається, що ентропія явно залежить тільки від енергії, об’єму і концентрації. Так як ці допущення використовуються в старих теоріях, то немає потреби виправдовувати можливість їх використання тут. Потрібно тільки порівняти результати термодинамічних розрахунків з розрахунками, виконаними за допомогою кінетичної теорії. Це було зроблено деякими авторами і особливо ретельно Пригожиним. Перше допущення з точки зору статистичної теорії є простий результат H-теореми. Перевірку справедливості другого допущення можна зробити, використовуючи теорію однорідного газу Чепмена і Енскога. У цій теорії функція розподілу швидкостей частинок виражається рядом

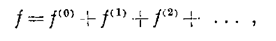(12)

де f₍₀₎ - максвел-больцманівський розподіл швидкостей, а f₍₁₎ f₍₂₎, ...- наступні наближення.

Строго кажучи, термодинамічні функції можуть бути точно визначені тільки при термостатичній рівновазі, коли f= f⁽⁰⁾. Тому очевидно, що допустимість використання таких параметрів, як ентропія і температура, обумовлюється властивістю збіжності ряду (12). Це означає, що зміна температури по довжині одного середнього вільного пробігу повинна бути набагато менша, ніж саме значення температури; це відноситься і до інших параметрів стану. Чисельне значення ентропії, температури і т. д. знаходиться так, ніби то раптово виділяється невеликий ізольований об'єм, за своїм станом порівнянний з усією системою, але включає достатнє число молекул і здатний забезпечити термостатичне рівновагу. Ця процедура втрачає сенс (зміст), якщо стан системи далекий від термостатичної рівноваги. Іншими словами, коли ряд (12) недостатньо швидко сходиться, макроскопічний опис системи унеможливлюється.

Точний зміст і теоретичні межі застосування рівняння Гіббса виявлені в розрахунках Пригожина, що відносяться до моделі Чепмена і Енскога. Ним було встановлено, що якщо знехтувати всіма членами ряду (12), крім першого, то результат розрахунку співпадає з результатом термостатичного розрахунку (ентропія не виникає). Використання двох членів ряду (12) дає точно такий же результат, як і термодинаміка необоротних процесів, що базується на рівнянні (11). Підстановка трьох членів ряду (12) призводить до результатів, відмінним від результатів і термодинамічних і кінетичних розрахунків. Цими розрахунками визначаються кількісні межі застосування термодинаміки незворотних процесів. Вони також показують, що ця теорія охоплює більш широку область явищ в порівнянні з термостатикою.