Individual tasks for PROBLEM 3.4
DRIVEN ELECTROMAGNETIC OSCILLATIONS.
In accordance with your variant to solve one of the following problems listed below (The number of problem statement and all necessary input data are reduced in the table 3.4).
1 Simple harmonic external EMF applied to the series oscillatory circuit of RLC-filter. Three nominal values of elements of filter and one equation of current or voltage oscillations in circuit are listed in the table 3.4. We used the following notations of quantities: ε – external EMF, i – public current in circuit, uR – voltage on resistor, uC – voltage on capacitor, uL – voltage on inductor.
1) To rebuild five equations of all five electric oscillatory quantities in circuit with numerical coefficients.
2) To build the vector voltage diagram at t=0.
3) To find the values of external EMF – ε, voltages – uR, uC , uL at the moment of time of t1 = Т/4 (Т – period of oscillations). To build the vector voltage diagram at t1 = Т/4.
2 Simple harmonic external EMF on the resonance frequency applied to the series oscillatory circuit of RLC-filter. Three nominal values of elements of filter and equation of current or voltage oscillations in circuit are listed in the table 3.4. We used the following notations of quantities: ε – external EMF, i – current in circuit, uR – voltage on resistor, uC – voltage on capacitor, uL – voltage on inductor.
1) To rebuild the equation of oscillations of all five quantities in circuit with numerical coefficients.
2) To build the vector voltage diagram at t=0.
3) To find the values of external EMF – ε, voltages – uR, uC , uL at the moment of time of t1 = Т/8 (Т – period of oscillations). To build the vector voltage diagram at t1 = Т/8.
TABLE OF TASK VARIANTS
Table 3.4
| Variant | Statement | С , mcF | L , mH | R , Ω | The equation of oscillations |
| i(t)=0,6×cos (2·104×t), А | |||||
| uR(t)=6×cos (500×t), V | |||||
| 12,5 | ε(t)=20×cos (ΩR×t), V | ||||
| 0,4 | 0,5 | uL(t)=5×cos (5·104×t), V | |||
| 1,5 | ε(t)=39,5×cos (2·104×t), V | ||||
| 0,1 | i(t)=1,5×cos (ΩR×t), А | ||||
| 0,05 | 7,5 | uC(t)=5×cos (2·105×t), V | |||
| 0,5 | 0,2 | uR(t)=15×cos (ΩR×t), V | |||
| 0,2 | i(t)=1,6×cos (2,5·104×t), А | ||||
| 0,5 | 0,15 | uL(t)=12×cos (2·105×t), V | |||
| uR(t)=30×cos (103×t), V | |||||
| 7,5 | uC(t)=20×cos (104×t), V | ||||
| ε(t)=19,3×cos (103×t), V | |||||
| 2,5 | uL(t)=50×cos (ΩR×t), V | ||||
| 0,5 | 0,2 | i(t)=0,6×cos (2·105×t), А | |||
| 0,5 | 0,05 | uC(t)=30×cos (ΩR×t), V | |||
| uR(t)=6×cos (2,5·103×t), V | |||||
| 0,2 | 1,5 | uC(t)=25×cos (105×t), V | |||
| ε(t)=4,5×cos (ΩR×t), V | |||||
| uL(t)=20×cos (104×t), V | |||||
| 0,1 | ε(t)=21,2×cos (5·104×t), V | ||||
| i(t)=2×cos (ΩR×t), А | |||||
| 0,25 | 1,5 | uR(t)=24×cos (4·104×t), V | |||
| uL(t)=3×cos (5·103×t), V | |||||
| 0,1 | 0,01 | uR(t)=6×cos (ΩR×t), V | |||
| uC(t)=20×cos (4·103×t), V | |||||
| 2,5 | 2,5 | ε(t)=29,7×cos (8·103×t), V | |||
| 0,5 | 0,8 | uL(t)=40×cos (ΩR×t), V | |||
| i(t)=0,8×cos (2·104×t), А | |||||
| 0,02 | 0,05 | uC(t)=25×cos (ΩR×t), V |
Problem 3.6.
ELECTROMAGNETIC WAVES (EMW).
MAIN CONCEPTS
When a plane EMW propagates from the source (which is located at point x0=0) along the positive direction of x-axis, the vector of electric field intensity will be changing along the y-axis, and the vector of magnetic field intensity will be changing along the z-axis, according to the equations of EMF:
| Ey(x,t)=Em×cos(wt–kx+j0); | (18) |
| Hz(x,t)=Hm×cos(wt–kx+j0), |
where Em and Hm – amplitudes of electric field intensity and magnetic field intensity in a wave correspondingly; j0 – initial phase of the wave source.
Cyclic frequency w [rad /s] – is a changing of phase of a wave per second:
w =2p /T =2pf , (19)
here T [s] – period is a time of one oscillation of waves’ quantities;
f [Hz] – frequency is a number of oscillations of waves’ quantities per second.
Wave number k [rad /m] – is a changing of phase a wave per meter:
k = 2p /l , (20)
here l [m] – wavelength is a length of one oscillation (distance which is transited by a wave for a period).
Phase velocity of propagation of EMW in medium
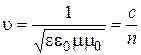 , (21)
, (21)
where speed of light (velocity of propagation of EMW in vacuum):
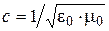 ; (22)
; (22)
and refractive index
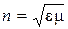 ; (23)
; (23)
e0 and m0 – electric and magnetic constants correspondingly;
e and m – relational electric permittivity and magnetic permeability of medium (as a rule the transparent medium is non-magnetic m=1).
In one EMW the volume density of energy of electric field wC is equal tovolume density of energy of magnetic field wL:
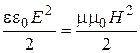 . (24)
. (24)
Instantaneous flux density of energy of EMW (Pointing’s vector)
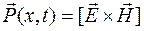 . (25)
. (25)
The average value of Pointing’s vector defines the wave intensity:
I=PAVE = Em×Hm / 2. (26)
EXAMPLE OF PROBLEM SOLUTION
Example 4. In the homogeneous isotropic non-magnetic medium with the dielectric permittivity of ε = 9 along the х-axis propagates plane EMW from wave source which is located at point x0=0. The change of intensity of magnetic field is described by equation Hz(x,t)=Hm×cos(wt–kx–p/2), when amplitude of magnetic field intensity in a wave 0,02 A/m. The oscillation period is1 ms.
1) To rebuild the equations of change of electric field intensity and magnetic field intensity with numerical coefficients.
2) To draw the graph of wave at the moment of time of t1=1,5T .
3) To define the Pointing’s vector at the moment of time of t1=1,5T in the point with coordinate x1 =1,25l and plot it on the graph.
4) To define the wave intensity.
| Input data: Нm = 0,02 A/m; Т =1 ms = 10 –6 s; ε = 9; μ = 1; Hz(x,t)=Hm×cos(wt–kx–p/2) | 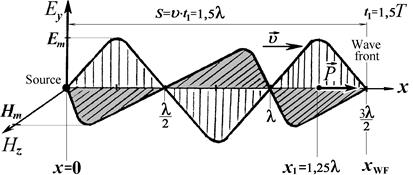 Figure 3.6 –Graph of wave at t1=1,5T . Figure 3.6 –Graph of wave at t1=1,5T . |
Find: Нz(x, t), Еy(x, t) – ? Graph , 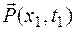 , I – ? , I – ? |
Solution:
1) Equations of given EMW have a general view:
Ey(x,t)=Em×cos(wt–kx+j0); Hz(x,t)=Hm×cos(wt–kx+j0),
where Em and Hm – amplitudes of intensities of electric and magnetic fields of the wave correspondently, x – coordinate of a point of space; t – time of propagation of a wave; j0= –p/2 – initial phase of the wave source.
For the rebuilding this equations with numerical coefficients, it’s necessary to define the cyclic frequency ω and wave number k, which are defined by equations:
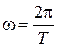 ; (4.1)
; (4.1)
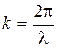 . (4.2)
. (4.2)
Period Т is given in the problem statement, the wave length λ is a distance which is transited by a wave for a period:
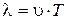 , (4.3)
, (4.3)
where u – phase velocity of propagation of EMW. In non-magnetic medium with permeability μ=1 and dielectric permittivity ε the velocity u of propagation of EMW is defined with the formula:
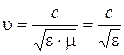 , (4.4)
, (4.4)
where с=3×108 m/s – the speed of light.
Let’s substitute in the formula (4.2) the expression of λ from the formula (4.3) and u from the formula (4.4):
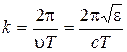 . (4.5)
. (4.5)
From the equality of volume energy density of electric and magnetic field
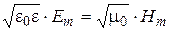 ,
,
we obtain the relation between the amplitudes of electric and magnetic intensities:
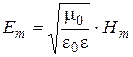 . (4.6)
. (4.6)
The right part of the formula (4.1) gives the unit of measurement of cyclic frequency [rad/s]; let’s check whether the right part of the formula (4.5) gives us the unit of wave number [rad/m], and right part of the formula (4.6) – the unit of intensity of electric field [V/m].
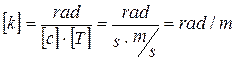 ;
;
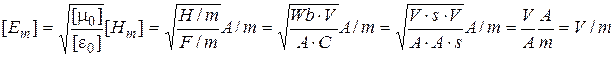
Let’s make the calculations and write down the equation Е and Н with numerical coefficients
 ;
; 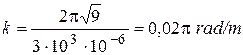 ;
;
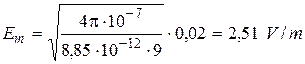 ;
;
Then finaly equations of EMW: Ey(x,t)=2,5×cos(2×106p×t–0,02p×x–p/2) V/m;
Hz(x,t)=0,02×cos(2×106p×t–0,02p×x–p/2) A/m.
2) Let’s draw the graph of wave at the moment of time of t1=1,5T.
At this time the source will have a phase, equal to
F(x=0,t1)= (2×106p×1,5×10 –6 – 0,02p×0– p/2)= (3p – 0– p/2)= p/2,
then intensities of electric and magnetic fields in a source will have a zero values, as a cos(p/2)=0 (Fig. 3.6, point x=0).
Through distance, equal to wave length
l= 2p / k or l= 2p / 0,02p=100m
this value will repeat, as a cos(p/2–kl)=0 (see Fig. 3.6, point x=l).
During this time the wave will transit distance equal to position of a wave front:
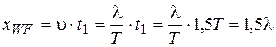 ,
,
then in position of wave front intensities of electric and magnetic fields in a source will have a values same as source at t=0, that is zero, as a cos(p/2–k×1,5l)=0 (see Fig. 3.6, point x=xWF).
3) Let’s Calculate instantaneous value of modulus of the Pointing’s vector (vector of energy fluxes density of EMW):
P(x,t)= Ey(x,t)×Hz(x,t)= Em×cos(wt–kx+j0)×Hm×cos(wt–kx+j0)= Em× Hm×cos2(wt–kx+j0).
Let’s check whether the obtained formula gives the unit of energy fluxes density [W / m2]
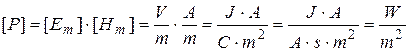 ;
;
Let’s substitute the numerical values:
P(x,t)= 2,5×0,02×cos2(2×106p×t–0,02p×x–p/2).
At the moment of time of t1=1,5T=10 –6s (given by the problem statement) and at the point with coordinate x1 =1,25l= 1,25×2p / k; then x1 =1,25×2p / 0,02p=125 m we obtain:
P(x1,t1) = 2,5×0,02×cos2(2×106p×1,5×10 –6 – 0,02p×125– p/2) =
= 0,05×cos2(3p – 2,5p– p/2) = 0,05×cos2(0,5p– p/2)= 0,05×(1)2=50 mW / m2.
Let’s plot it on the graph obtained Pointing’s vector (see Fig. 3.6, point x=x1 =1,25l).
4) The intensity of electromagnetic wave is the average energy in time, going through the unit plane, which is perpendicular to the direction of wave propagation;
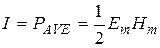 ,
,
where Р – average value of vector modulus of energy fluxes density of EMW (modulus of Pointing’s vector).
Let’s make the calculations: I = 0,5·2,51·0,02= 2,51·10-2 W / m2 = 25 mW / m2.
Results: Ey(x,t)=2,5×cos(2×106p×t–0,02p×x–p/2) V/m;
Hz(x,t)=0,02×cos(2×106p×t–0,02p×x–p/2) A/m.
P(x1,t1) =50 mW / m2; I = 25 mW / m2.
