Дискретность квантовых состояний, опыт Франка и Герца, интерпретация опыта; квантовые переходы, коэффициенты Эйнштейна для квантовых переходов. Связь между ними.

Дискретность квантовых состояний.

Внутренняя энергия атомов не может изменяться непрерывно, а изменяется скачками, т.е. атом может обладать лишь энергией из некоторого дискретного ряда значений. Это обстоятельство выражается также словами, что энергия атома квантуется.

Если характеризовать состояние атома его энергией, то можно сказать, что состояния атома дискретны.

Опыт Франка и Герца.

Постулаты Бора нашли свое экспериментальное подтверждение в опытах Франка и Герца. Идея опыта заключалась в том, что пучок электронов, ускоряемых в электрическом поле, проходил через газ и электроны испытывали соударения с атомами газа. Схема опытов изображена на рисунке. Накаленный катод К, испускающий электроны, сетчатый электрод S и анод А, соединенный с гальванометром, помещались в стеклянный сосуд, в котором находились ртутные пары при низком давлении. Электроны, ускоренные электрическим полем, могут испытывать упругие (в результате которых энергия электронов не изменяется, а изменяются скорость и направление движения) и неупругие (связаны с передачей энергии электронов атомам ртути) соударения с атомами ртути. При втором типе соударений атом может воспринять лишь определенную энергию и перейти в одно из возбужденных состояний.

Ближайшим к нормальному состоянию атома ртути является возбужденное состояние, отстоящее от основного по шкале энергий на 4.86 эВ.

Если энергия электрона < 4.86 эВ, то они испытывают лишь упругие столкновения и анодный ток возрастает. Как только кинетическая энергия электронов достигает 4.86 эВ, начинают происходить неупругие столкновения. Электрон полностью отдает энергию атому ртути, возбуждая переход из нормального состояния на энергетический уровень. Электрон, потерявший энергию не может преодолеть задерживающее поле и не достигнет анода. Таким образом, должно происходить резкое падение анодного тока. Аналогичные явления будут происходить при значениях энергий электронов 2*4.86 3*4.86 … n*4.86.

На рис. приведена кривая I( ), -- разность потенциалов, ускоряющего электрического поля, подтверждающая справедливость первого постулата Бора.

Правило частот Бора также подтвердилось в опытах Франка и Герца. Ртутные пары, возбужденные электронным ударом, оказались источником ультрафиолетового излучения. Это излучение происходит, когда атом ртути, возбужденный электронным ударом с энергией W₂, возвращается в исходное состояние с энергией W₁. Согласно правилу частот Бора 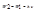. Т.е. 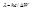( 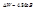). Сравнивая результаты приходим к выводу, что теория согласуется с экспериментом.

Квантовые переходы.

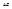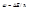Каждое из состояний атома характеризуется своей энергией. При переходе в другое состояние с меньшей энергией разность энергий испускается в виде кванта света, частота которого связана с энергией соотношением . Может быть также совершен переход из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией, но для этого необходимо, чтобы энергия 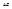была сообщена атому извне. Это случается при поглощении атомом кванта света частотой .

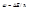Коэффициенты Эйнштейна.

Пусть существует уровень n с энергией E_n и уровень m с энергией E_m, при чем E_n>E_m. С уровня n на уровень m возможны и спонтанные (обусловленные внутренними причинами), и вынужденные переходы (обусловленные внешними по отношению к атому причинами), а обратно только вынужденные. Пусть A_nm – отнесенная к единице времени вероятность, что атом из состояния n спонтанно перескакивает в состояние m, излучив фотон энергии 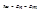. Если N_n – концентрация атомов на уровне n, то в единице времени в единице объема спонтанно на уровень m перейдет число атомов

.

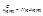Пусть B_nm – отнесенная к единице времени и единице спектральной плотности излучения вероятность того, что атом из состояния m вынужденно, под воздействием внешнего поля излучения, перейдет в состояние n, излучив фотон энергии 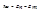. Число атомов, вынужденно перешедших в единицу времени с уровня n на уровень m

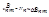
Наконец, пусть B_mn – отнесенная к единице времени и единице спектральной плотности излучения вероятность того, что атом вынужденно перейдет с уровня m на уровень n с поглощением кванта 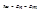. Очевидно, что если N_m – концентрация атомов на уровне m, то единицу времени в единице объема на уровень n вынужденно перейдет число атомов

.

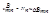Величины A_nm, B_nm, B_mn называется коэффициентами Эйнштейна.

42. Ядерная модель атома.

Ядерная модель атома приписывала атому строение, аналогичное строению Солнечной системы, в центре которой находится положительно заряженное ядро, вокруг которого, подобно планетам , движутся электроны, удерживаемые у ядра силами кулоновского притяжения.

Действительное строение атома мог выяснить только эксперимент, задача которого состояла в том, чтобы определить распределение электрического заряда в атоме.

Формула Резерфорда.

Точечные заряды взаимодействуют по закону Кулона. Рассмотрим теорию рассеяния на силовом кулоновском центре. Рассмотрим движение частицы с массой 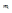и зарядом 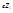в кулоновском поле другой частицы с 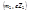. Будем считать, что , так, что вторую частицу можно считать неподвижной. Используя закон сохранения момента импульса 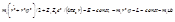, где 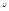-скорость рассеиваемой частицы на бесконечность, b-прицельное расстояние, т.е. расстояние наименьшего сближения частиц, если бы взаимодействиемежду ними отсутствовало. Точками обозначены производные по времени.

Введем новую независимую переменную 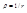и учтем, что 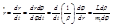. Тогда по первой формулы 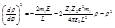. Дифференцируя это выражение по 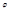, получим для определения 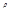уравнение 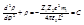, общее решение которого 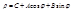. При условиях 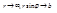при 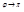можно найти 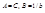, тогда уравнение примет вид 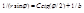. Полагая, что 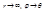, находим угол рассеяния: 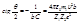. Перейдем к статическим характеристикам рассеяния. Дифференциальное поперечное сечение 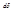упругого рассеяния в угол между 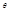и 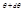определяется как отношение числа частиц 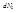, рассеянных в угол между 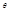и 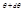к потоку падающих частиц N: 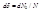. Отсюда следует, что все частицы, прицельные расстояния которых заключены между b и b+db, будут рассеяны в угол между 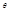и . Число частиц с прицельным расстоянием между b и b+db равно числу частиц, падающих на кольцевую площадь радиусом b и шириной db: 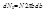. Дифференциальное поперечное сечение 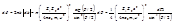. Здесь 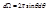- телесный угол между конусами с углам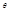и и 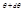. Эта формула называется формулой Резерфорда. С ее помощью Резерфорд проанализировал результаты своих опытов по рассеянию 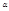-частиц на атомах и установил структуру атомов.

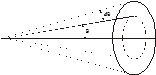
Опыты Резерфорда.

Для своих опытов Резерфорд воспользовался 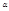-частицами, которые вылетают из атомов радиоактивных элементов. 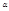-частица является ядром атома гелия, т.е. несет с собой положительный заряд 2e и имеет массу, равную примерно 4-м массам протона. Поэтому для анализа рассеяния 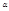-частиц воспользуемся формулой Резерфорда с 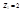.масса атомов, на которых рассеиваются 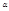-частицы, предполагается намного больше массы 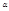-частиц.

От этого ограничения легко освободиться, если под массой 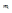понимать массу системы из двух взаимодействующих частиц. Пучок 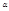-частиц известной интенсивности направляется на тонкую мишень, где они рассеиваются на атомах этой мишени. Число -частиц, рассеиваемых на различные углы, подсчитывается с помощью специальных счетчиков. Формулой Резерфорда определяется число частиц, рассеянных одним рассеивающим центром. Если число этих центров равно n, то число рассеянных в телесный угол 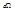частиц равно 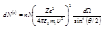, где Ze – заряд ядра рассеивающего атома. Если зафиксировать телесный угол 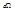=const, в котором подсчитываются частицы под различными углами рассеяния 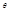, то из последней формулы получаем 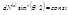. В эксперименте было проверено соблюдение последнего условия(формулы). Оказалось, сто хотя каждый из сомножителей в левой части равенства изменялся в 1000 раз, их произведение оставалось постоянным. Это означает, что формула(предпоследняя) правильно описывает рассеяние и роль многократных рассеяний несущественна.

Несовместимость планетарной модели атома с классическими представлениями.

Благодаря наличию центростремительного ускорения у движущихся вокруг ядра электронов они должны непрерывно излучать электромагнитные волны. В результате потери энергии они должны упасть на ядро, т.е. планетарной модели существовать не может. С точки зрения классической физики частота излучения атома должна совпасть с частотой обращения электронов. Такой характер спектра излучения полностью противоречит наблюдаемым закономерностям атомных спектров. С классической точки зрения электрон может описывать вокруг ядра всевозможные орбиты. Идея о дискретном ряде возможных орбит электрона находится в глубоком противоречии с классической планетарной моделью. Революционный шаг по устранению этих противоречий был сделан Бором.