Вычисление термодинамических величин с помощью плотности одночастичных стационарных состояний.

При описании идеального ферми-газа можно придерживаться следующего алгоритма.

Сначала находим базис одночастичных стационарных состояний, т.е. стационарных состояний одной отдельно взятой частицы, рассмотренной в тех же самых внешних силовых полях, что и весь газ.

Далее, используя формулу (34), находим плотность одночастичных стационарных состояний.

Затем подставляем плотность одночастичных стационарных состояний в уравнение (42) для химического потенциала. Решив это уравнение, находим химический потенциал.

Далее, зная плотность одночастичных стационарных состояний и химический потенциал, находим свободную энергию с помощью выражения (41).

Наконец, зная свободную энергию, находим нужные макроскопические характеристики нашего идеального ферми-газа.

Рассмотрим теперь газа невзаимодействующих тождественных бозонов.

Микростояния газа тождественных невзаимодествующих бозонов определяются аналогично тому, как это делалось в случае идеального ферми-газа. Точно также в стационарном состоянии всего нашего газа в целом каждая из частиц находится в одном из одночастичных стационарных состояний. Поэтому также как и в случае системы невзаимодействующих тождественных фермионов микросостояние идеального бозе-газа задается совокупностью чисел заполнения 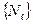всех одночастичных стационарных состояний.

Точно также, как и в случае ферми-газа, энергия микросостояния нащего бозе-газа с данной совокупностью чисел заполнения 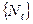есть сумма по всем микросостояниям от произведения энергии одночастичного стационарное состояние на число частиц в этом одночастичном стационарном состоянии

, (43)

а среднее число частиц равно сумме чисел заполнения

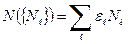, (44)

А вот волновые функции микросостояний ферми- и бозе-газа принципиально отличаются. В случае газа невзаимодействующих тождественных фермионов волновая функция любого микросостояния антисимметрична относительно перестановки частиц, т.е. при перестановке двух частиц она меняет знак. Именно эта антисимметрия приводит к фундаментальному ограничению на значения чисел заполнения - принципу запрета Паули. В случае же газа невзаимодействующих тождественных бозонов симметрия волновой функции иная: она является симметричной относительно перестановки частиц, т.е. при перестановке двух частиц волновая функция бозе-газа не меняется. Поэтому в газе невзаимодействующих тождественных бозонов нет фундаментального ограничения на числа заполнения, подобного принципу запрета Паули.

Также как и раньше нам нужно, найти выражение для среднего числа частиц в данном одночастичном стационарном состоянии и свободную энергию нашего бозе-газа.

Для того, чтобы это сделать нужно в точности повторить те выкладки, которые мы сделали для идеального ферми газа, только заменив в них сумму на сумму .

В результате мы получим, что в идеальном бозе-газе химический потенциал не может быть положительным (в противном случае сумма будет расходиться), а среднее число частиц в одночастичном стационарном состоянии дается выражением

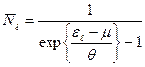. (45)

Для свободной энергии мы получим следующее выражение

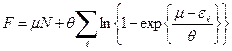. (47)

Эта функция 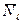называется функцией распределения Бозе-Эйнштейна.

Плотность одночастичных стационарных состояний свободного идеального электронного газа в отсутствие внешних полей. Химический потенциал, внутренняя энергия и давление при абсолютном нуле температуры.

Установим физический смысл величины 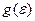. Проинтегрируем ее по конечному интервалу

. (37)

Изменив порядок интегрирования и суммирования, и воспользовавшись основным свойством дельта-функции Дирака, находим

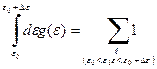. (38)

Из полученного выражения легко видеть, что 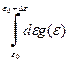есть число одночастичных стационарных состояний с энергией, попадающей в интервал . Следовательно, величина 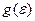представляет собой число одночастичных стационарных состояний, приходящихся на единичный интервал энергии. По этой причине функция 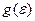называется плотностью одночастичных стационарных состояний.

При переходе к записи через плотность одночастичных состояний мы, фактически, сумму по квантовым числам одночастичных состояний заменяем интегралом по энергии, а под знаком интеграла пишем произведение плотности одночастичных состояний на ту функцию одночастичной энергии, которая стояла под знаком суммы.

Это мнемоническое правило, на самом деле, является общим. Проведя проедуру, аналогичную только что проделанной, можно показать следующее. Пусть есть некоторая функция одночастичной энергии. Тогда

. (39)

Например, свободная энергия идеального ферми-газа дается выражением

. (40)

В данном случае функция . В соответствие с нашим мнемоническим правилом сумму по квантовым числам заменяем интегралом по энергии. Под знаком интеграла пишем произведение плотности одночастичных состояний на функцию , стоящую под знаком суммы

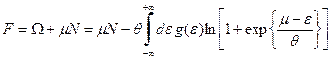. (41)

В состоянии равновесия число частиц в нашем газе слабо колеблется около своего среднего значения, практически всегда с ним совпадая. В пределах точности термодинамики этими флуктуациями можно пренебречь и считать, что число частиц в газе является постоянным, равным этому среднему значению. В дальнейшем мы будем рассматривать ситуации, когда число частиц в газе известно. В таком случае состояние равновесия нашего газа удобно задавать удобно задавать, указывая температуру 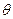, внешние параметры 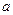и число частиц 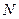, а химический потенциал рассматривать как величину, определяемую уравнением

. (42)

Можно легко показать, что при заданных значениях 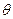, 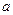и 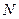уравнение (42) относительно химического потенциала имеет единственный вещественный корень. Поэтому химический потенциал нашего газа можно рассматривать как однозначную функцию 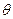, 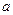и .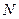

И. г. Ферми — Дирака отличается от классического тем, что даже при абсолютном нуле температуры его давление и плотность энергии отличны от нуля и тем больше, чем выше плотность газа. При абсолютном нуле температуры существует максимальная (граничная) энергия, которую могут иметь частицы И. г. Ферми — Дирака (так называемая Ферми энергия). Если энергия теплового движения частиц И. г. Ферми — Дирака много меньше энергии Ферми, то его называют вырожденным газом.