В стационарном случае уравнение Шредингера имеет вид

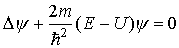где Е, U - полная и потенциальная энергия, m - масса частицы.

8, Для того, чтобы покинуть поверхность твердого или жидкого тела электрону необходимо преодолеть потенциальный барьер, то есть совершить работу.Минимальная энергия, которую надо затратить, чтобы удалить электрон из твердого или жидкого вещества в вакуум (в состояние сравной нулю кинетической энергией), называется работой выхода электрона.

10, Метод Юнга. Источником света служит ярко освещенная щель S (рис. 245), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂,параллель­ные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источников.

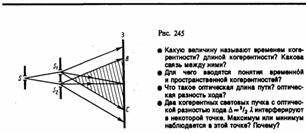
Интерференционная картина (область ВС) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S₁ и S₂. Как уже указывалось, Т. Юнгу принадлежит первое наблюдение явления интерференции.

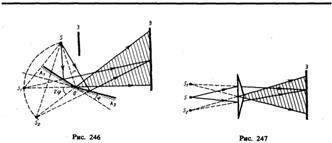
2. Зеркала Френеля. Свет от источника S (рис. 246) падает расходящимся пучком на два плоских зеркала А₁О и А₂О, расположенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол j мал). Используя правила построения изображения в плоских зеркалах, можно показать, что и источник, и его изображения S₁ и S₂ (угловое расстояние между которыми равно 2j) лежат на одной и той же окружности радиуса r с центром в О (точка соприкосновения зеркал).

Световые пучки, отразившиеся от обоих зеркал, можно считать выходящими из мнимых источников S₁ и S₂, являющихся мнимыми изображениями S в зеркалах. Мнимые источники S₁ и S₂ взаимно когерентны, и исходящие из них световые пучки, встречаясь друг с другом, интерферируют в области взаимного перекрывания (на рис. 246 она заштрихована). Можно показать, что максимальный угол расхождения перекрывающихся пучков не может быть больше 2j.Интерференционная карти­на наблюдается на экране (Э), защищенном от прямого попадания света заслон­кой (З).

3. Бипризма Френеля. Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S (рис. 247) преломляется в обеих призмах, в результате чего за бипризмой распространяются световые лучи, как бы исходящие из мнимых источников S₁ и S₂,являющихся когерентными. Таким образом, на поверхности экрана (в заштрихованной области) происходит наложение когерентных пучков и наблюдается интерференция.

11, Соотношение неопределенностей имеет вид (в проекциях на координатные оси):

(16)

где 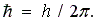Соотношение неопределенностей определяет допустимый принципиальный предел неточностей координат D x, D y, D z и значений проекций импульсов D p_x, D p_y, D p_z, которые характеризуют состояние микрочастицы. Чем точнее определена координата x (малое значение D x), тем с меньшей точностью возможно охарактеризовать проекцию импульса p_x(большое значение D p_x), и наоборот.

Билет 9

1,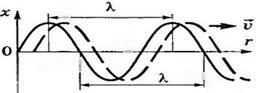

Расстояние между ближайшими точками, колеблющимися в одинаковых фазах (рис. 15.7), называется длиной волны. Длина волны 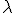равна расстоянию, на которое распространяется фронт волны за время, равное периоду 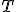колебаний источника волн: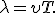

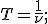
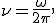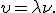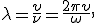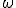Так как то скорость волны связана с частотой колебаний уравнением Отсюда где — циклическая частота колебани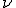й, и 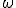зависят только от свойств источника волны.

2, 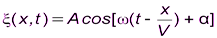или .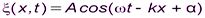

3, Интерференция волн — взаимное усиление или ослабление амплитуды двух или нескольких когерентных волн, одновременно распространяющихся в пространстве.^[1] Сопровождается чередованием максимумов и минимумов (пучностей) интенсивности в пространстве. Результат интерференции (интерференционная картина) зависит от разности фаз накладывающихся волн.

4, Условие Вульфа — Брэгга определяет направление максимумов дифракции упруго рассеянного на кристалле рентгеновского излучения. Выведено в 1913 независимо У. Л. Брэггом и Г. В. Вульфом. Имеет вид:

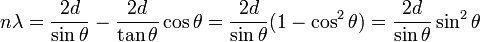
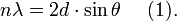
где d — межплоскостное расстояние, θ — угол скольжения (брэгговский угол), n — порядок дифракционного максимума, λ — длина волны.

5, Атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определённая энергия E_n. В стационарном состоянии атом не излучает.

6, 0,+ - 1

7,Вы́нужденное излуче́ние, индуци́рованное излучение — генерация новогофотона при переходе квантовой системы (атома, молекулы, ядра и т. д.) из возбуждённого в стабильное состояние (меньший энергетический уровень) под воздействием индуцирующего фотона, энергия которого была равна разности энергий уровней. Созданный фотон имеет те же энергию, импульс, фазу и поляризацию, что и индуцирующий фотон (который при этом не поглощается). Оба фотона являются когерентными.

8, Внутренняя энергия появляется в них при повышении температуры (например, при комнатной температуре уровень энергии теплового движения атомов равняется 0,4·10⁻¹⁹ Дж), и отдельные атомы получают энергию для отрыва электрона от атома. С ростом температуры число свободных электронов и дырок увеличивается, поэтому в полупроводнике, не содержащем примесей, удельное сопротивление уменьшается.

10,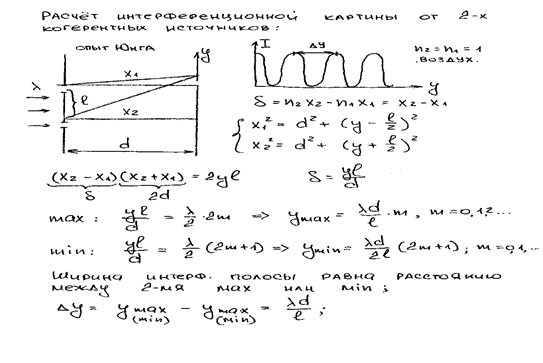

11, Ква́нтовая меха́ника — раздел теоретической физики, описывающий физические явления, в которых действие сравнимо по величине спостоянной Планка. Предсказания квантовой механики могут существенно отличаться от предсказаний классической механики. Энергетическая светимость АТЧ пропорциональна четвертой степени его термодинамической температуры:

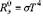, где σ-- постоянная Больцмана. Этот

закон – закон Стефана-Больцмана.

Следствие ф-лы Планка. Согласно квантово теории Планка, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями -- квантами, причем энергия ванта пропорциональна частоте колебания

Постоянная Планка.

Закон Вина. Опираясь на законы термо- и электродинамики, Вин установил зависимость длины волны λmax , соответствующей максимуму функции rλ,T , от температуры Т. Согласно закону смещения Вина,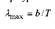

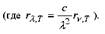
Вывод формулы Планка для абсолютно чёрного тела

Выражение для средней энергии колебания с частотой ω дается выражением:

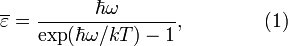
где 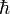— постоянная Планка, — постоянная Больцмана.

Количество стоячих волн в трёхмерном пространстве равно:

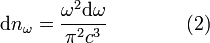
Билет 10

1, Длина волны - это расстояние между ближайшими точками, колеблющимися в одинаковых фазах.

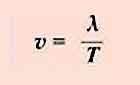
2,
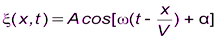или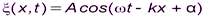

3, Скорость распространения света в воздухе почти не отличается от скорости света в вакууме: с 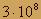м/с.Если свет попадает из вакуума в какую-нибудь среду, то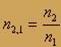

где n - абсолютный показатель преломления данной среды. Относительный показатель преломления двух сред связанный с абсолютными показателями преломления этих сред, где 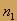и 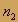- соответственно абсолютные показатели преломления первой и второй сред.

4, Принцип Гюйгенса — Френеля формулируется следующим образом:

Каждый элемент волнового фронта можно рассматривать, как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

5, Закон Брюстера — закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера.

Закон Брюстера: 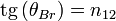, где n12 — показатель преломления второй среды относительно первой, θBr — угол падения (угол Брюстера).

6, Красная» грани́ца фотоэффе́кта — минимальная частота или максимальная длина волны света, при которой еще возможенвнешний фотоэффект, то есть начальная кинетическая энергия фотоэлектронов больше нуля. Частота зависит только от работы выхода электрона:

7, Соотношение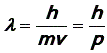

аналогичное уравнению (14), где p = mv – импульс частицы, определяет длину волны любой частицы,