Число ошибок такого вида В4 для блока из lхn символов равно

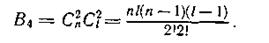
Общее число четырехкратных ошибок составляет

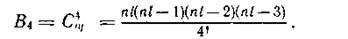
Таким образом, отношение числа не обнаруживаемых четырехкратных ошибок к общему числу таких ошибок

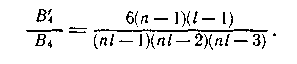
Определим минимальный вес ненулевого вектора рассматриваемого итеративного кода (двумерной кодовой комбинации). Такой вектор должен содержать только одну ненулевую вектор-строку, минимальный вес, которой равен 2. Проверка на четность каждого из ненулевых столбцов также дает вектор веса 2. Следовательно, минимальный вес ненулевого вектора итеративного кода с двойной проверкой на четность равен 2*2 = 4.

Аналогично можно показать, что в общем случае минимальный вес вектора итеративного кода равен произведению минимальных весов векторов итерируемых кодов. Так как минимальное кодовое расстояние для линейного кода равно минимальному весу его ненулевых векторов, то минимальное расстояние итеративного кода равно

где dγ — кодовое расстояние линейного кода по координате γ.

Коррекция ошибок проводится последовательно. Сначала исправляют ошибки по одной координате, затем осуществляют исправление оставшихся ошибок по другой координате и т. д.

Такая процедура проста, но снижает корректирующую способность итеративного кода, поскольку оказывается невозможным исправить часть ошибок кратности (d-l)/2.

Поясним это на примере итерации двух кодов Хэмминга (7, 4). Результирующий итеративный код (49, 16) имеет минимальное кодовое расстояние, равное 3x3 = =9, и, следовательно, потенциально, как любой линейный код, способен исправлять все ошибки кратности 4 и менее. Однако, применяя указанную выше процедуру декодирования, невозможно исправить четырехкратные ошибки с расположением искаженных символов в вершинах прямоугольника (рис. 6.26).

Специальные двухстепенные коды. Специальные двухстепенные коды нашли широкое применение для обнаружения и исправления ошибок, возникающих при записи, хранении и считывании цифровой информации с накопителей на магнитном носителе, например на магнитной ленте. Разработанные коды базируются на исследованиях статистики ошибок. Опубликованные данные показывают, что при эксплуатации магнитных носителей преобладают пачки ошибок вдоль дорожек (столбцов), причем вероятность возникновения двух пачек ошибок и более на разных дорожках в кадре информации из нескольких десятков строк достаточно мала.

Рассмотрим один из таких кодов [4].

Стандартный код для записи информации на магнитную ленту. В каждом кадре информации формируется одна дополнительная строка. Проверочные символы на дополнительной дорожке определяются из условия обеспечения нечетности числа единиц вдоль данной строки. В направлении дорожек используется параллельный циклический код, позволяющий определить номер дорожки, на которой возникла пачка ошибок. Зная номер дорожки с искаженными символами и используя результаты проверок по строкам, можно произвести их исправление.

Расположение кодируемого кадра информации на ленте показано на рис. 6.27.

Кодирование циклическим кодом осуществляется следующим образом. Многочлен F1(x), соответствующий информации перкой строки, умножается на x и результат приводится по модулю образующего многочлена g(x) степени n, где n — число дорожек, включая контрольную [например, для 9 дорожек g(x) = (х + 1)(х⁸ + + х⁴ + х³ + x² + 1)]. Полученный остаток R_i(x) суммируется по модулю два с многочленом F2(x), соответствующим информации второй строки. Сумма снова умножается на x и далее приводится по модулю g(x), в результате чего определяется остаток R₂(x). Применив этот алгоритм последовательно ко всем строкам кодируемого кадра информации, получим R₁(x) — многочлен степени не выше n-1, который и записывается в конце кадра (при нечетном числе строк в нем), в качестве символов контроля по дорожкам

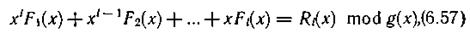
где R_i(x) mod (x) означает величину R_i(x), приведенную по модулю g(x).

Декодирование производится аналогично кодированию, причем участвует и контрольная строка — R_i(x). Процесс декодирования можно записать следующим образом:

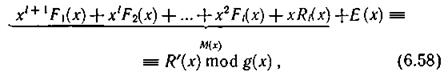
где Ε (x) — некоторый многочлен, определяющий ошибку. Выражение M(х) можно представить в виде

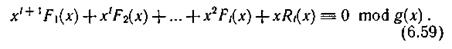
Сравнивая его с выражением (6.58), можно заключить, что при отсутствии ошибки будет фиксироваться значение R'(x), равное нулю. Случай R'(x) неравна 0 соответствует обнаружению ошибки. Если имела место пачка ошибок вдоль одной из дорожек, то она может быть исправлена. Многочлен ошибки в этом случае имеет вид Ε (x) = x^je(х), где е(х) отражает поразрядную структуру, а х^j — адрес ошибки. Так как справедливо равенство (6.59), то

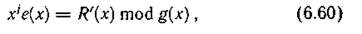
причем е(х) определяется по результатам проверок строк на нечетность.

Номер дорожки с искаженными символами может быть найден теперь, исходя из следующих соображений. Предположив, что на ленте была записана информация, состоящая из одних нулей, т. е. F₁(x) = 0...F_l(x) = 0, R_l(x) = 0 и при считывании на дорожке с выбранным известным номером n возникла пачка ошибок с точно такой же структурой е(х), в результате декодирования получим некоторый многочлен R"(x), причем

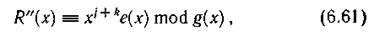
где k — число дорожек, на которое отстоит дорожка с известным номером η от дорожки, где возникла пачка ошибок.

Таким образом, если пачка ошибок возникла только по одной дорожке, то, умножив R'(x) на x^k с приведением по модулю g(x), получим R"(x). Поэтому при декодировании одновременно с вычислением R'(x) осуществляется вычисление R"(x). Для определения номера дорожки с искаженными символами производится последовательное домножение R'(x) на х, х², ..., х^n-1.

На каждом шаге, начиная с R'(x), результат приводится по модулю g(x) и затем сравнивается с R"(x). Процесс прекращается, как только на каком-либо i-м шаге зафиксировано равенство (в этом случае k = i— 1 и известная величина n определяет номер искомой дорожки) или после проведения n сравнений. В последнем случае фиксируется наличие неисправимой ошибки.

При четном числе строк кодируемой информации l образующий многочлен типа g(x) = (х + 1 )g'(x) обеспечивает R_l(x) всегда с четным числом членов. Суммирование этого многочлена с g'(x) позволяет получить результирующий многочлен R'_l(x), удовлетворяющий проверке по нечетности вдоль строки.

Описанные коды способны исправлять все пачки ошибок, возникающие по одной дорожке, за исключением пачек вила

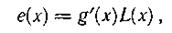
где L(x) — произвольный многочлен.

Кодирование и декодирование информации с использованием рассматриваемых кодов относительно просто реализуется как программными, так и аппаратными средствами [4].

§ 6.11 СВЕРТОЧНЫЕ КОДЫ

Для сверточных (рекуррентных) кодов характерно, что операции кодирования и декодирования осуществляются над непрерывной последовательностью символов. Такой метод имеет определенные преимущества, так как предоставляет большие возможности для использования вводимой избыточности.

В общем случае сверточному кодированию могут подвергаться последовательности символов, являющихся элементами произвольного конечного поля GF(q). Мы ограничимся рассмотрением двоичных сверточных кодов. Принцип кодирования поясняется рис. 6.28. В каждый дискретный момент времени на вход кодирующего устройства поступают k информационных последовательностей символов, а с его выхода в канал связи выдаются η последовательностей, причем n>k. Проверочные символы, как и в блоковых кодах, получаются в результате проведения линейных операций над определенными информационными символами.

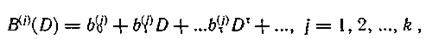
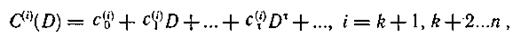
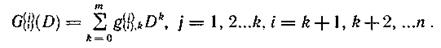
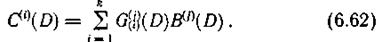
Если первые k выходных последовательностей совпадают со входными, сверточный код называется систематическим.

Способы реализации сверточных кодов во многом похожи на способы реализации циклических кодов.

Процессы кодирования и декодирования таких кодов можно описать посредством многочленов с использованием оператора задержки D. Последовательности символов, поступающие на каждый из входов, представляют многочленами, где c_t⁽ⁱ⁾— символ, появляющийся на j-м выходе кодирующего устройства в момент τ.

Связь между информационными и проверочными символами задается образующими многочленами сверточного кода.

Степени образующих многочленов не превышают числа т, а коэффициентами Mjk для двоичных кодов являются элементы поля GF(2).

Последовательности проверочных символов образуются как линейные комбинации последовательностей информационных символов

где b_t⁽ⁱ⁾ — символ j-и информационной последовательности, поступившей в момент τ.

Последовательности проверочных символов также можно записать в виде многочленов

В процессе прохождения по каналу связи передаваемые символы могут искажаться. Запишем последовательности информационных и проверочных символов, поступивших из канала связи, в виде многочленов и

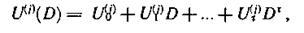
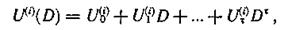
здесь U_t⁽ⁱ⁾ символ j-й информационной последовательности, поступившей в момент τ(j=1,2,…,k); U_t⁽ⁱ⁾ — символ i-й проверочной последовательности, поступившей в момент τ(i= k+l, k + 2, ...,n).

Аналогично запишем последовательности ошибок, содержащие единицы на местах искаженных символов и нули во всех остальных позициях:

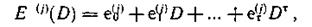
где e_t^(j) — символ ошибки, имеющей место в j'-й информационной последовательности в момент τ (у = 1, 2, ..., k).

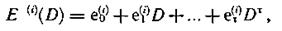
где e_t⁽ⁱ⁾ — символ ошибки, имеющей место в i-й проверочной последовательности в момент τ (i = k + 1, k + 2, ..., n).

Очевидно,

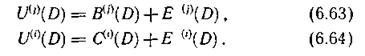
В процессе декодирования по информационным символам, поступающим из канала связи, с использованием образующих многочленов снова формируются последовательности проверочных символов U_l⁽ⁱ⁾(D)

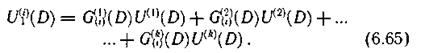
Последовательности U_l⁽ⁱ⁾(D) и U⁽ⁱ⁾(D) (i = k+l, k + 2, ..., n) сравниваются между собой, в результате чего получаем последовательности S⁽ⁱ⁾(D), определяющие структуру ошибок. Эти последовательности по аналогии с блоковыми кодами называют синдромами

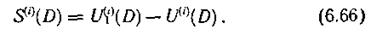
Подставляя выражения (6.63) и (6.64) в (6.66), получаем

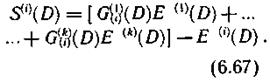
В соответствии со структурой синдромов строится вторая часть декодирующего устройства — узел коррекции ошибок. Существуют сверточные коды, рассчитанные как на исправление взаимно независимых ошибок, так и пачек ошибок.

Использование сверточных кодов возможно и при последовательной передаче символов. В этом случае несколько последовательностей информационных символов могут быть сформированы из одной входной последовательности посредством коммутатора. На выходе кодирующего устройства информационные и сформированные проверочные символы аналогичным синхронным коммутатором вновь объединяются в одну последовательность.

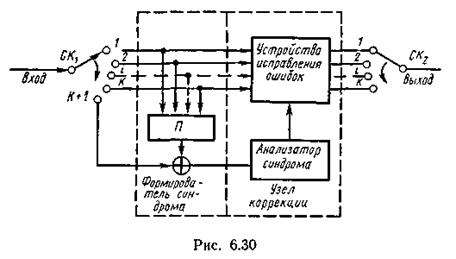
На рис. 6.29 приведена схема кодирующего устройства для простейших сверточных кодов, у которых на k информационных символов приходится один проверочный. За время цикла входной коммутатор СК₁ направляет k символов входной последовательности в k информационных каналов, с которых они поступают как непосредственно на выход, так и на линейный преобразователь П, формирующий проверочный символ C_k+1· В случае двоичного кодирования преобразователь включает ячейки памяти, объединенные в регистры сдвига, устройства умножения на постоянную величину (связи) и сумматоры по модулю два. Ячейки памяти позволяют добиться усреднения влияния помехи при малых n за счет использования символов, поступающих на соседних циклах.

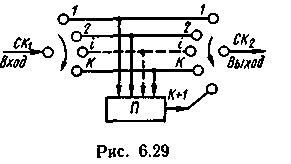
В декодирующем устройстве (рис. 6.30) информационные символы последовательности, поступающей из канала связи, также разделяются с помощью коммутатора CK₁ по k информационным каналам. Посредством линейного преобразователя П, аналогичного преобразователю кодирующего устройства, снова формируются проверочные символы C_k+1, которые сравниваются (суммируются по модулю два) с проверочными символами, поступающими непосредственно из канала связи. В случае отсутствия ошибок образующаяся на выходе последовательность символов состоит из одних нулей.

Очевидно, что в процессе сравнения единица в синдроме может и не образовываться, если одновременно окажется искаженным не только информационный символ, но и проверочный, сформированный с участием данного информационного символа. Чтобы исключить такую возможность, информационные и соответствующие им проверочные символы разносятся в канале по времени передачи, что осуществляется посредством ячеек памяти преобразователя. Предполагается, что за пачкой ошибок следует определенное число неискаженных символов. Поэтому одновременное искажение информационных и зависящих от них проверочных символов считается невозможным. Если же длина пачки ошибок превысит значение, на которое рассчитывается код, или между пачками ошибок не будет необходимого числа неискаженных символов, то сверточный код не обеспечивает исправления ошибок. Более того, в этом случае может произойти «исправление» правильно принятого информационного символа на неправильный. Анализатор синдрома, входящий в состав блока коррекции, представляет собой логическую схему, определяющую, к какой информационной последовательности относится очередной искаженный символ, и формирующую соответствующий импульс коррекции.

Устройство исправления ошибок включает сумматоры по модулю два для каждого информационного канала и буферные регистры, расположенные как до, так и после сумматоров, для выравнивания временных задержек, возникающих при формировании и анализе синдрома. Выходная последовательность исправленных информационных символов формируется синхронным коммутатором СК₂.

Пример 6.27. Рассмотрим процессы кодирования и декодирования простейших сверточных кодов, разработанных Д. В. Хагельбаргером.

Для формируемых этим кодом последовательностей характерно, что за каждым информационным символом следует проверочный символ (n = 2, k= 1). Коды способны исправлять пачку ошибок длиной <l символов при условии, что две соседние пачки разделены между собой защитным промежутком 3l+1 символов, т.е. между последним символом данной пачки и первым символом следующей пачки должно быть не менее 3l+ 1 неискаженных символов.

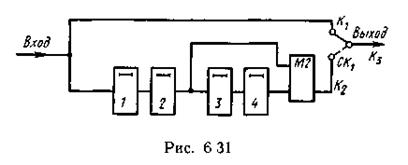Для конкретности примем l<4. Кодирующее устройство такого кода (рис. 6.31) представляет собой схему умножения на образующий многочлен G(D) = D² + D⁴ (см. рис. 6.11). Будем считать, что на вход поступает последовательность информационных символов (точка Κι) 100100111001, что соответствует многочлену B(D) = 1 + D³ + D⁶ + +D⁷+D⁸ + D¹¹.

Помножив B(D) на образующий многочлен G(D), получим многочлен C(D), соответствующий последовательности проверочных символов, формируемых в точке К₂:

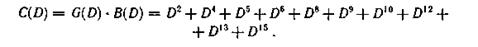
Процесс формирования проверочных символов кодирующим устройством показан в табл. 6.25.

Таблица 6.25

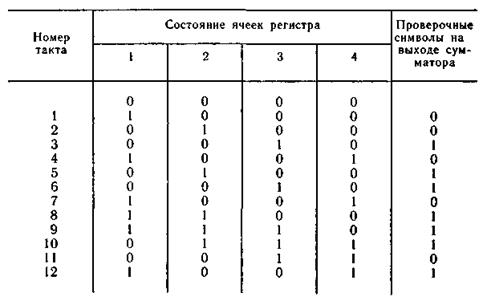
При последовательной передаче с выхода коммутатора будут поступать попеременно информационные символы последовательности 1001001110010000 и проверочные символы из последовательности 0010110111011101, образуя на входе канала связи последовательность (в точке К₃) 10000110010110111101001101010001.

Предположим, что в канале связи произошло искажение 7, 8 и 9-го символов. Последовательность на выходе канала связи (точка K₄) имеет вид 100001 101101111010011, где искаженные символы помечены прямоугольником.

Последовательность информационных символов в декодирующем устройстве (точка K₅) 100010111001 соответствует многочлену

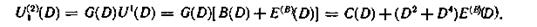
а последовательность проверочных символов 0011110111011 — многочлену U⁽²⁾(D)= = G(D) + С^(c)(D), где E^(c)(D) = =D³.

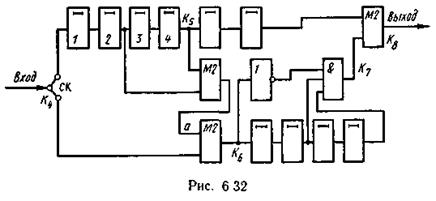
Декодирующее устройство (рис. 6.32) состоит из двух частей: первая часть вырабатывает опознаватель ошибки (синдром), а вторая — анализирует синдром и производит само исправление (узел коррекции).

Проверочная последовательность, формируемая в точке α декодирующего устройства по принятой последовательности информационных символов, выражается многочленом

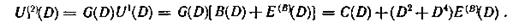
Процесс ее формирования показан в табл. 6.26. Сформированная в точке a последовательность сравнивается с последовательностью проверочных символов, поступающих из канала связи, в результате чего на выходе (точка К₆) вырабатывается опознаватель ошибки — синдром S(D):

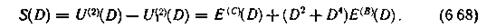
Таблица 6.26

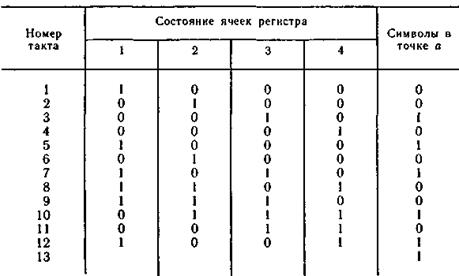
Он не зависит от информационных символов и определяется только видом пачки ошибок. В случае отсутствия ошибок эта последовательность состоит из одних нулей. Учитывая, что в пачке ошибок из четырех символов два символа информационных и два проверочных, легко расшифровать структуру синдрома.

Первые две позиции в синдроме характеризуют искажения в проверочных символах (E^(c)(D)), затем две позиции характеризуют искажения в информационных символах (D²E^(b)(D)), а в следующих двух позициях предыдущие значения повторяются ( D⁴E^(b)(D)).

Убедимся, что последовательность в точке K₆ декодирующего устройства соответствует полученному синдрому. Она равна сумме по модулю два последовательности в точке a и последовательности поступивших из канала проверочных символов

Полученная последовательность действительно соответствует

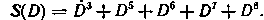Анализатор синдрома построен в точном соответствии с его структурой.

Повторение в синдроме символов, соответствующих ошибкам в информационной последовательности, позволяет опираться при их выделении на логический элемент И. С учетом того, что коррекция целесообразна лишь в случае, когда за пачкой ошибок следуют неискаженные символы, используют элемент И на три входа.

На первый его вход через элемент НЕ поступает инвертированная последовательность символов синдрома; на второй — символы синдрома, задержанные на два такта; на третий — символы синдрома, задержанные на четыре такта.

На выходе элемента И получаем последовательность импульсов коррекции, исправляющих поступившую последовательность информационных символов Запишем эти последовательности:

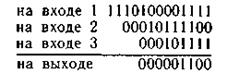
Так как корректирующий сигнал формируется через 3l/2, а информационные символы задерживаются только на l тактов, то возникает необходимость в дополнительной задержке информационных символов на l/2 тактов (l/2 = 2) Это осуществляется блоком задержки. Совместно с сумматором по модулю два он образует устройство исправления ошибок:

последовательность в точке K₅ 100010111001

последовательность в точке Κ₇ 00000110000000

исправленная последовательность

информационных символов

(точка K₈) 00100100111001

Сверточные коды для записи информации на магнитную ленту. Рассмотрим процедуру образования сверточных кодов применительно к исправлению пачек ошибок на магнитной ленте. Коды строятся в предположении появления пачек ошибок вдоль дорожек, причем считается, что вероятность возникновения нескольких пачек ошибок на разных дорожках в кадре информации из нескольких десятков строк весьма мала, что обычно соответствует статистическим данным об ошибках.

Сверточные коды для указанной цели можно построить, используя идею Ивадари [20], обобщающую подход к декодированию сверточных кодов Д. В. Хагель-баргера. В рассмотренном нами примере имела место одна информационная последовательность и структура синдрома выражалась соотношением (6.68).

В основу декодирования сверточных кодов, рассчитанных на несколько входных информационных последовательностей, также кладется принцип совпадения повторяющихся частей синдрома. Однако для возможности определения информационной последовательности, в которой возникла пачка ошибок, между повторяющимися частями синдромов включается различное число нулевых символов.

Таким образом, информационным последовательностям в синдроме соответствуют конфигурации веса второго вида:

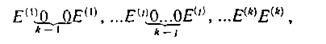
где E^(j) — последовательность двоичных символов, соответствующая пачке ошибок, возникшей в j-и информационной последовательности.

Для проверочной последовательности имеем единственную конфигурацию веса первого вида E^(k+1) 0...0. Конфигурации в синдроме кода должны быть размещены так, чтобы они не накладывались друг на друга, обеспечивая их безошибочное выделение при декодировании.

Для сверточного кода, рассчитанного на исправление пачек ошибок длины l при считывании с накопителя, имеющего k0 информационных дорожек и одну проверочную n₀ = (k₀+1), общее выражение для синдрома информационной последовательности имеет вид

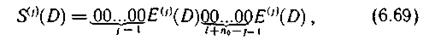
где E^(j)(D) — двоичная последовательность, соответствующая пакету длины l, возникшему на j-и дорожке (1<=j<=k₀).

Аналогичное выражение для синдромов ошибок на контрольной дорожке имеет вид

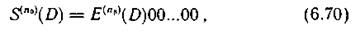
где E⁽ⁿ⁰⁾(D) — двоичная последовательность, соответствующая пакету ошибок длиной l, возникшему на контрольной дорожке.

Связь между символами синдрома и символами принятой последовательности задается посредством выражения (6.67), считая, что на всех дорожках, кроме j-и, пакеты ошибок отсутствуют (соответствующие E(D) нулевые), синдромы S⁽ⁿ⁰⁾(D) для различных j можно представить в виде

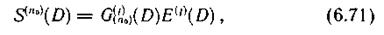
где G_(n0)^(j)(D) — образующие многочлены сверточного кода.

Подберем G_(n0)^(j)(D) так, чтобы при возникновении последовательности ошибок E^(j)(D) синдром S⁽ⁿ⁰⁾ (D) соответствовал выражению 1.

Указанным требованиям удовлетворяет образующие многочлены вида

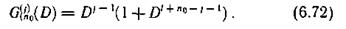
Защитный промежуток построенного кода

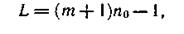
здесь m — наибольшая степень образующего многочлена.

Описанные коды строились в предположении, что для размещения контрольных символов используется только одна дорожка. Для случая, когда имеется возможность разместить контрольные символы на двух дорожках, на основе идей сверточного кодирования можно построить коды, позволяющие исправлять пакеты произвольной длины по одной дорожке и требующие значительно меньшего защитного промежутка. Техническая реализация таких кодов весьма проста.

Для построения кода К₀ информационных последовательностей, поступающих на вход кодера, представим в виде

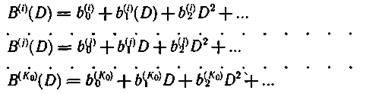
Для формирования контрольной последовательности выберем образующие многочлены в соответствии с выражением (6.72). Принимая l=0, получим следующую совокупность образующих многочленов:

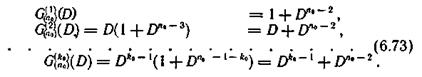
Подставляя образующие многочлены (6.73) в выражение для контрольной последовательности, получим значения символов этой последовательности, которая имеет вид

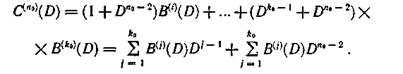
Таким образом, при выбранных образующих многочленах контрольную последовательность символов С⁽ⁿ⁰⁾(D) можно представить в виде двух последовательностей, которые при n₀ — k₀ = 2 могут быть записаны на две контрольные дорожки. Тогда по одной дорожке фиксируется последовательность

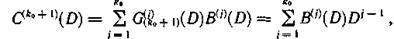
а на другой контрольной дорожке — последовательность

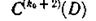
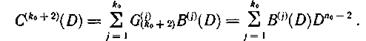
Рассмотрим процесс исправления ошибок. Запишем общие выражения для синдромов ошибок каждой из контрольных последовательностей

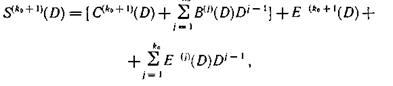
где

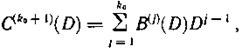
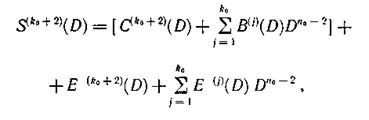
где

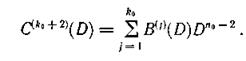
Тогда

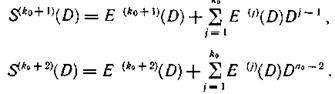
Поскольку предполагается, что пакеты ошибок возникают только по одной дорожке, один из синдромов определяет начало пакета и его структуру и, следовательно, дает информацию о виде многочлена ошибки Ε (D). Структура другого синдрома в этом случае должна иметь вид E(D)D^j-1. Для определения номера дорожки, где расположен пакет ошибок, последовательно домножаем Ε (D) на D и сравниваем с другим синдромом. Значение j, при котором наступает равенство, указывает номер искомой дорожки.

Процесс образования контрольных символов имеет простое толкование. Если совокупность образующих код многочленов, участвующих в формировании символов контрольной последовательности С^(k0+1)(D), записать в виде

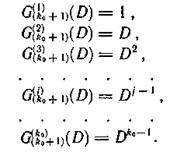
а совокупность образующих многочленов, участвующих в формировании символов контрольной последовательности G^(k0+2)(D), в виде

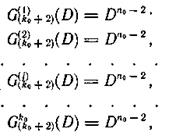
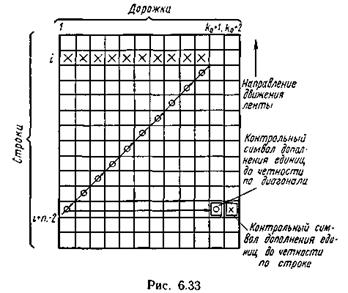то наглядно выступает закономерность, выражающаяся в том, что символы первой контрольной последовательности образуются в результате суммирования символов, расположенных по диагонали, а символы второй контрольной последовательности образуются в результате суммирования символов строки массива. Такой код можно назвать кодом с проверкой на четность по строке и диагонали (рис. 6.33).

Простая геометрическая интерпретация процессов формирования контрольных символов, безусловно, является еще одним существенным преимуществом данного кода, поскольку не требуется никакой математической подготовки для понимания механизма коррекции ошибок. Наиболее неблагоприятный случай в отношении определения величины защитного промежутка возникает, когда предыдущий пакет ошибок располагается на первой дорожке, а последующий пакет — на k₀ дорожке. Наибольший защитный промежуток при этом равен

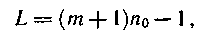
где т — наибольшая из степеней образующих многочленов.

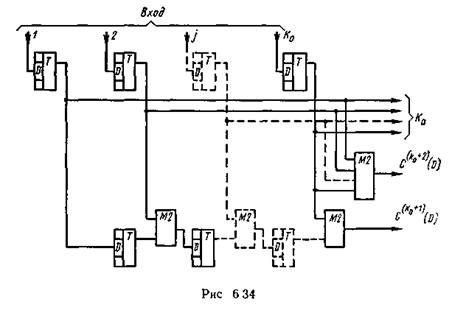
Для реализации разработанного кода требуется простая аппаратура с буферной памятью, емкостью &0по разрядов. Схема кодирующего устройства приведена на рис. 6.34, а схема декодирующего устройства — на рис. 6.35. Поскольку процесс кодирования не требует пояснений, остановимся только на процессе декодирования.

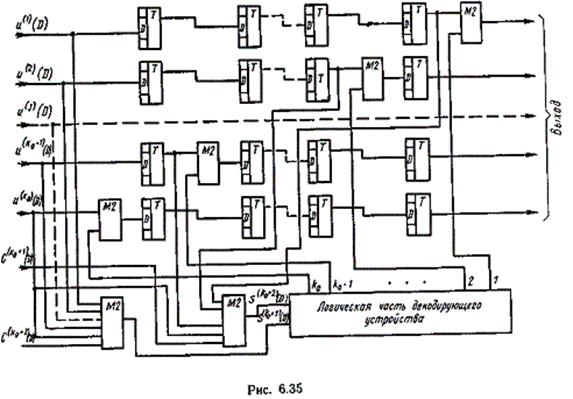
Сигналы, соответствующие символам принятых информационных последовательностей (U^(j)(D)), по тактам поступают в буферное ЗУ, которое состоит из регистров сдвига и сумматоров по модулю два, расположенных по диагонали буферного ЗУ. Одновременно производится образование символов синдрома S^(k0+1)(D) и S^(k0+2)(D). Символы конкретного синдрома S^(k0+2)(D) образуются посредством сложения по модулю два принятых символов строки, включая контрольные символы дополнения по четности. Символы конкретного синдрома 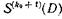образуются посредством сложения по модулю принятых символов, расположенных по диагонали массива, включая контрольные символы дополнения по четности.

Сигналы, соответствующие символам синдромов 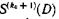и 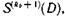поступают в логическую схему, где формируются сигналы коррекции (рис. 6.36).

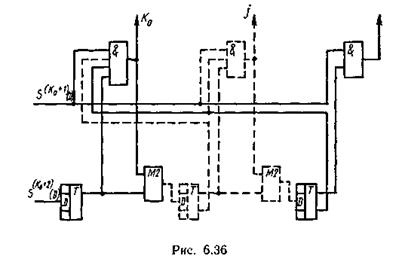Сигналы, соответствующие символам синдрома 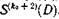подаются на вход регистра сдвига логической схему и при отсутствии сигналов ошибки по диагонали продвигаются через сумматоры по модулю два вдоль регистра синхронно с принятыми сигналами, соответствующими информационным символам.

В случае обнаружения ошибки по диагонали получаем сигнал, соответствующий ненулевому символу синдрома 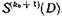, который воздействует на схему И логической части устройства декодирования. На выходе той схемы И, на которую одновременно воздействуют сигналы ошибок по строке и диагонали, возникает сигнал коррекции. Поскольку предполагается одна ошибка в строке, сигнал ошибки после формирования сигнала коррекции далее по регистру не продвигается.

Сигналы коррекции подаются в соответствующие сумматоры по модулю два, расположенные в диагонали буферного ЗУ, и ошибка исправляется.

Контрольные вопросы

1. Сформулируйте и поясните основную теорему Шеннона о кодировании для канала с помехами.

2. Какова причина целесообразности кодирования длинных последовательностей символов?

3. Какие коды называют помехоустойчивыми?

4. За счет чего помехоустойчивый код получает способность обнаруживать и исправлять ошибки?

5. Охарактеризуйте блоковые и непрерывные, разделимые и неразделимые помехоустойчивые коды.

6. Что подразумевают под кратностью ошибки?

7. Как определяется минимальное кодовое расстояние?

8. Запишите соотношения, связывающие минимальное кодовое расстояние с числом обнаруживаемых и исправляемых ошибок.

9. Назовите основные показатели качества корректирующего кода.

10. Дайте определение понятий группы, подгруппы, смежного класса.

11. В чем различие понятий кольца и поля?

12. Как определяется линейное векторное пространство?

13. Какой помехоустойчивый код называют линейным?

14. Что понимают под вектором ошибки?

15. Что такое опознаватель ошибки?

16. Как составляется таблица опознавателей для конкретной совокупности корректируемых векторов ошибок?

17. Как по таблице опознавателей записать равенства, в соответствии с которыми определяются значения проверочных разрядов?

18. В чем сущность мажоритарного декодирования?

19. Дайте определение порождающей матрицы кода.

20. Какой код называют систематическим?

21. Как построить проверочную матрицу кода?

22. Каким требованиям должен удовлетворять образующий многочлен циклического кода?

23. Дайте определение понятий идеала в кольце и класса вычетов по идеалу.

24. Как находят опознаватели ошибок в случае циклического кода?

25. Что такое выделенный синдром?

26. Какие устройства составляют основу технической реализации циклических кодов?

27. Нарисуйте схему кодирующего устройства циклического кода и поясните ее работу.

28. Поясните процесс декодирования циклического кода.

29. Определите поле классов вычетов по модулю образующего многочлена.

30. Какой элемент поля классов вычетов называется примитивным?

31. Как распределяются корни двучлена хⁿ+1 по составляющим неприводимым многочленам?

32. Как выбрать образующий многочлен кода Боуза — Чоудхури — Хоквингема?

33. В чем заключается методика декодирования кодов Боуза — Чоудхури — Хоквингема?

34. Какими характерными особенностями обладают итеративные коды?

35. Объясните процедуру исправления пачки ошибок кодом, используемым в накопителях на магнитной ленте.

36. Назовите условие правильного исправления ошибок при применении рекуррентного кода?

ЗАКЛЮЧЕНИЕ

Изложенные в учебнике идеи и методы теории информации представляют интерес не только в плане решения задач, связанных с передачей и хранением информации. Теоретико-информационный подход приобрел значение метода исследования, позволяющего качественно и количественно сопоставлять специфические характеристики конкретных устройств и систем независимо от их физической сущности.

С использованием теоретико-информационных представлений построены новые более общие модели известных явлений и решен ряд практически важных задач в таких областях, которые при создании теории информации не принимались во внимание.

Можно отметить, например, такие задачи, как определение общей оценки качества измерения быстроизменяющихся величин (проблему динамической погрешности) в измерительной технике, информационная трактовка процессов стабилизации, отработка управляющих воздействий и адаптация в технике автоматического управления, разработка оптимальных алгоритмов поиска неисправностей в технике автоматического контроля, освещение информационных аспектов процессов естественного отбора и наследственности, включая вопросы помехоустойчивого кодирования генетической информации в биологии, выявление информационной сущности механизма возникновения эмоций в психологии и т. п.

Широкое проникновение идей и методов теории информации в различные области науки и техники вполне естественно, поскольку информация является характеристикой такого всеобщего свойства материи, как разнообразие.

В свою очередь, различные приложения теории способствуют ее дальнейшему развитию, например, в направлении учета ценности информации и других аспектах.

Следует ожидать, что идеи и методы теории информации будут успешно использоваться и в дальнейшем, особенно при создании сложных систем, объединяющих различные по целям, функциям и даже физическому воплощению подсистемы.

СПИСОК ЛИТЕРАТУРЫ

1. Винер Η. Кибернетика.

2. Герасименко В. А., Мясников В. А. Защита информации от несанкционированного доступа. — М.: МЭИ, 1984.

3. Глушков В. М. Мышление и кибернетика//Вопросы философии, 1963. № 1. С. 10—24.

4. Дмитриев В. И. Учебное пособие по курсу «Теория информации и кодирования». — М.: МЭИ, 1977.

5. Дмитриев В. И., Иванов А. В. Новые сверточные коды для исправления ошибок на магнитной ленте//Труды МЭИ. Вып. 495. 1980. С. 11 — 17.

6. Дэвис Д. и др. Вычислительные сети и сетевые протоколы. — М.: Мир, 1982.

7. Зиновьев А. Л., Филиппов Л. И. Введение в теорию сигналов и цепей. — М.: Высшая школа, 1975.

8. Игнатов В. А. Теория информации и передачи сигналов.—М.: Советское радио, 1979.

9. Колесников В. Д , Мирончиков Е. Т. Декодирование циклических кодов. — М.: Связь, 1968.

10. Колмогоров А. Н. Три подхода к определению понятия «количество информации»//Проблемы передачи информации. 1965. Т. 1. Вып. 1. С. 25—38.

11. Коган И. М. Прикладная теория информации. — М.: Радио и связь, 1981.

12. Кузьмин И. В., Кедрус В. А. Основы теории информации и кодирования. — Киев: Высшая школа, 1977.

13. Кузьмин И. В., Явна А А., Ключко В. И. Элементы вероятностных моделей АСУ. — М.: Советское радио, 1975.

14. Липкин И. А. Основы статистической радиотехники, теории информации и кодирования — М.: Советское радио, 1978.

15. Логинов В. М. и др. Экономичное кодирование. — Киев.: Техника, 1976.

16. Мамиконов А. Г. Управление и информация. — М.: Наука, 1975.

17. Мельников Ю. Н. Достоверность информации в сложных системах. — М.: Советское радио, 1973.

18. Новик А. А. Эффективное кодирование. — М: Энергия, 1965.

19. Пенин П. И. Системы передачи цифровой информации. — М: Советское радио, 1976.

20. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976.

21. Пугачев В. С. Теория случайных функций и ее применение к задачам автоматического управления. — М.: Изд-во технико-теоретической литературы, 1957.

22. Основы кибернетики. Теория кибернетических систем/Под ред. К. А. Пупкова. — М.: Высшая школа, 1976.

23 Советов Б. Я. Теория информации. — Л.: Изд. ЛГУ, 1977.

24. Солодов А. В. Теория информации и ее применение к задачам автоматического управления и контроля. — М.: Наука, 1967.

25. Тарасенко Ф. П. Введение в курс теории информации. — Томск: Изд. ТГУ, 1963.

26. Темников Ф. Ε. и др. Теоретические основы информационной техники. — М.: Энергия, 1979.

27. Теория кодирования. Сборник. — М.: Мир, 1964.

28. Фельдбаум А. А. и др. Теоретические основы связи и управления. — М.: Физматгиз, 1963.

29. Финк Л. М. Теория передачи дискретных сообщений. — М.: Советское радио, 1970.

30. Харкевич А. А. Борьба с помехами. — М.: Физматгиз, 1965.

31. Хартли Р. Передача информации. Теория информации и ее приложения/Под ред. А. А. Харкевича. — М.: Физматгиз, 1959.

32. Хемминг Р. В. Теория кодирования и теория информации. — М.: Радио и связь, 1983.

33. Хетагуров Я. А., Руднев Ю. П. Повышение надежности цифровых устройств методами избыточного кодирования. — М.: Энергия, 1974.

34. Хинчин А. Я. Об основных теоремах теории информации// //УМН. 1956. № 1 (67). С. 17—75.

35. Четвериков В. Н. Преобразование и передача информации в АСУ. — М.: Высшая школа, 1974.

36. Шеннон К. Работы по теории информации и кибернетике. — М.: ИЛ, 1963.

ПРИЛОЖЕНИЯ

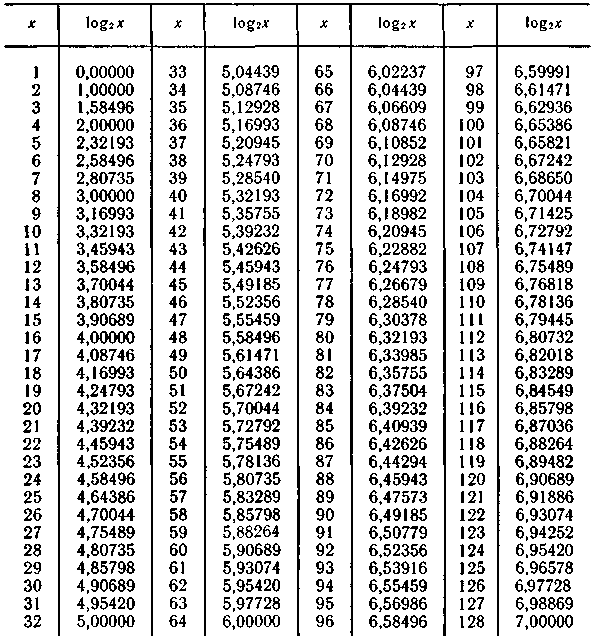
Таблица П.1 Двоичные логарифмы чисел от 1 до 128

Продолжение табл. П.2

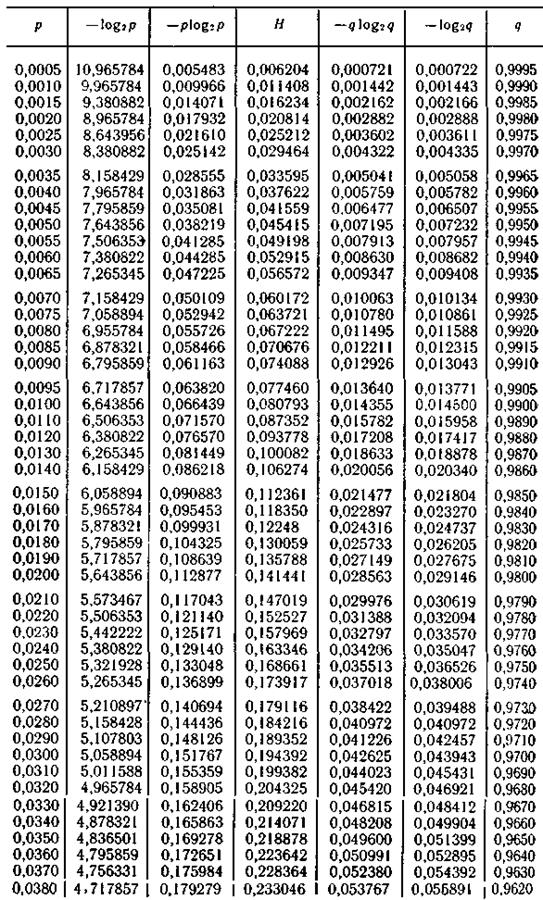
Продолжение табл. П.2

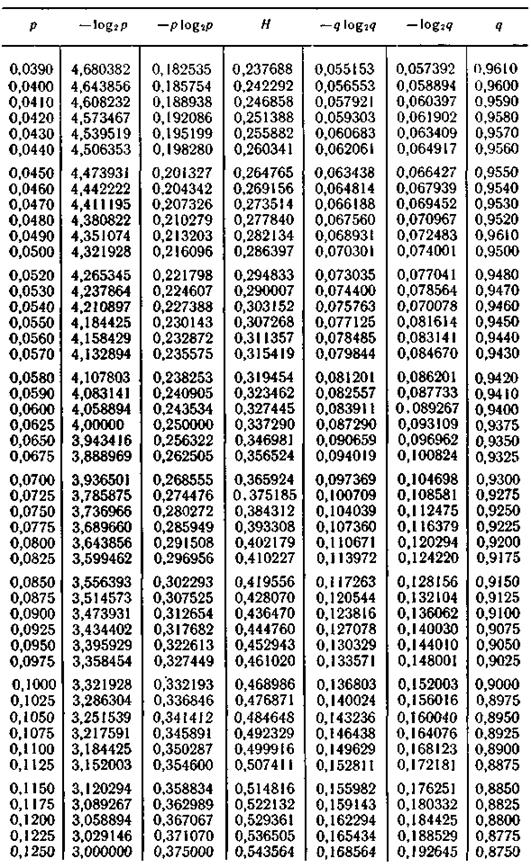
Продолжение табл. П.2

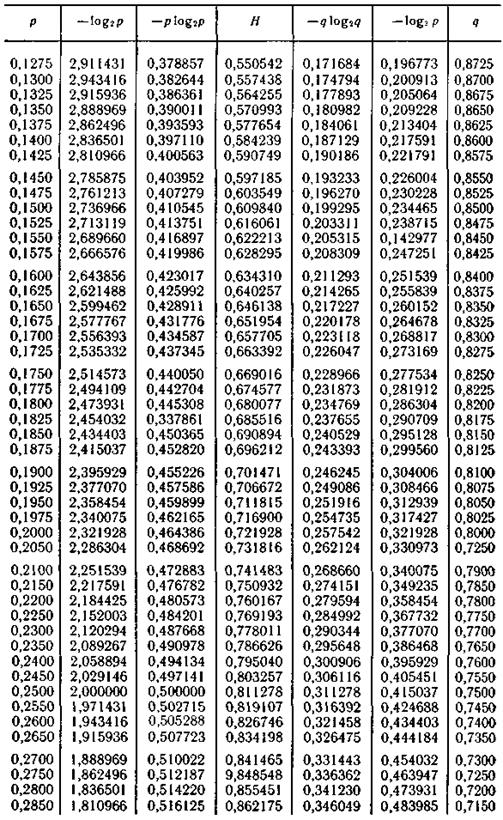
Продолжение табл. П.2

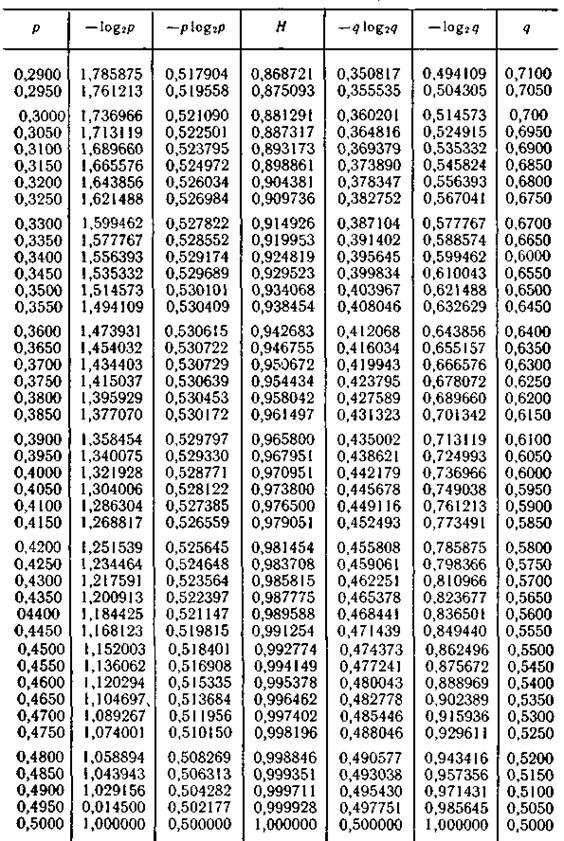
Таблица П.3 Таблица многочленов, не приводимых над полем GF(2)

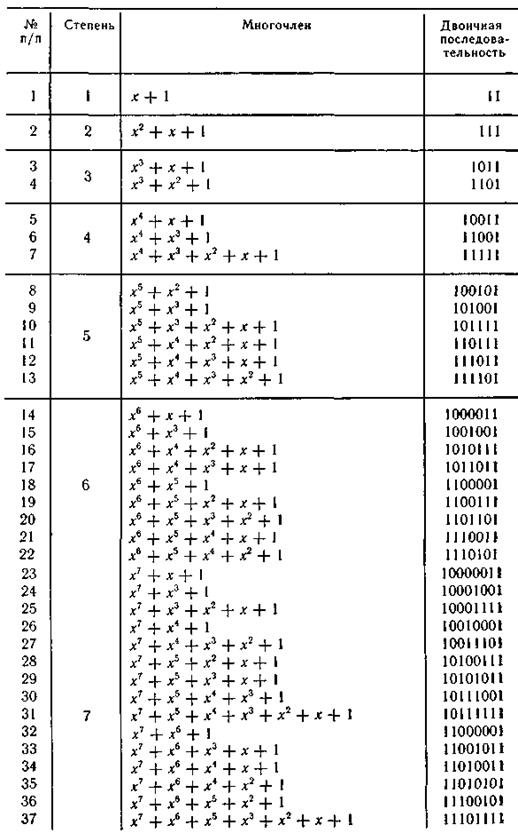
Продолжение табл. П.3