Задача 6. Показати, що земна атмосфера не може перебувати в статистичній рівновазі і безупинно розсіюється в простір

Розв’язання. Густина ідеального газу в потенціальному полі визначається розподілом Больцмана:

,

де - густина газу у тих точках, де .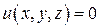

Гравітаційне поле Землі визначається законом тяжіння Ньютона, де потенціальна енергія u прямує до нуля на нескінченності. Це призводить до того, що густина у скільки завгодно далеких точках повинна бути скінченною величиною згідно з розподілом Больцмана. Але ж для скінченного числа N частинок це неможливо. Тобто в гравітаційному полі Землі атмосфера не може перебувати в рівновазі і повинна безперервно розсіюватися в простір. Формально ця ситуація відповідає тому, що статистичний інтеграл для газу в такому гравітаційному полі розбігається.

Задача 7. Визначити розподіл чисельної густини ідеального газу з частинок у центрифузі радіуса і довжини , що обертається з кутовою швидкістю . Температура газу . Обчислити середню потенціальну енергію молекул газу.

Розв’язання. У системі координат, що зв’язана з центрифугою, діятиме відцентрова сила . Потенціальна енергія 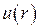молекули в полі цієї сили становитиме

,

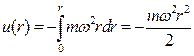де відстань r відраховується від осі обертання. Тому густину газу згідно з розподілом Больцмана можна записати у вигляді

(1)

Сталу А знаходимо з умови нормування

,

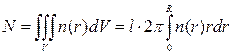звідки

. (2)

Середня потенціальна енергія молекул газу, яка припадає на одну молекулу дорівнюватиме

,

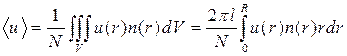що з урахуванням (1) та (2) остаточно дає

.

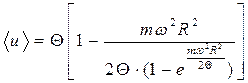Задача 8. Потенціальна енергія електрона всередині металу менше його енергії поза металом на величину . Визначити густину струму термоелектронної емісії, якщо концентрація електронів у металі дорівнює .

Розв’язання. Враховуючи, що енергія вільного електрона в металі менша за його енергію зовні металу на величину роботи виходу , а також припускаючи, що електрони підлягають розподілу Максвелла, густину струму вздовж вісі ОХ (перпендикулярно поверхні металу) запишемо як середнє від 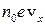за розподілом (1), наведеним у задачі 1:

, (1)

де швидкість 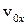визначається з умови виходу електрона з металу: 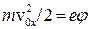. Отже, інтегруючи (1), остаточно знаходимо

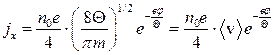, (2)

де 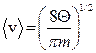- середня швидкість електронів за розподілом Максвелла (див. формулу (3) першої задачі). До речі, (2) є класичною формулою Річардсона для густини струму термоелектронної емісії.

Задача 9. Розріджений газ знаходиться в посудині під тиском . Визначити швидкість витікання газу у вакуум через невеликий отвір площею при максвеллівському розподілі молекул газу за швидкостями.

Розв’язання. Ця задача повторює другу частину задачі 4, оскільки повне число молекул, які падають за 1 с на 1 см² стінки (густина потоку n) є таким же їх числом, що виходять з посудини крізь 1 см² отвору за 1 с. Тобто швидкість витікання 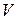молекул крізь отвір з перетином дорівнюватиме 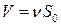, де n визначається за формулою (3) задачі 4. Отже, враховуючи, що 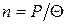, остаточно

.
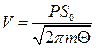