Яка у випадку однорідного поля являє собою доцентрову силу
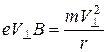 , (12.2)
, (12.2)
де 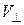 – складова швидкості електрона, перпендикулярна вектору
– складова швидкості електрона, перпендикулярна вектору 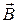 , е – заряд, m – маса електрона.
, е – заряд, m – маса електрона.
Сила Лоренца примушує електрон рухатися вздовж кола в площині, перпендикулярній 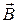 . Радіус кола r визначається зі співвідношення (12.2)
. Радіус кола r визначається зі співвідношення (12.2)
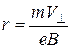 . (12.3)
. (12.3)
На поздовжню складову швидкості 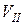 сила Лоренца не впливає. Складова швидкості
сила Лоренца не впливає. Складова швидкості 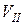 переміщує електрон вздовж вектора
переміщує електрон вздовж вектора 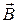 (вздовж осі z, рис.12.1). Отже електрон прийматиме участь у двох рухах – вздовж кола зі швидкістю
(вздовж осі z, рис.12.1). Отже електрон прийматиме участь у двох рухах – вздовж кола зі швидкістю 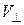 та в напрямку поля зі швидкістю
та в напрямку поля зі швидкістю 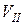 . В результаті електрон рухатиметься вздовж гвинтової лінії, крок якої дорівнює
. В результаті електрон рухатиметься вздовж гвинтової лінії, крок якої дорівнює
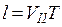 . (12.4)
. (12.4)
Період Т в (12.4) можна знайти зі співвідношення
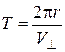 , (12.5)
, (12.5)
або, використовуючи вираз для r (12.3), отримуємо
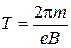 . (12.6)
. (12.6)
Із співвідношень (12.4), (12.5) випливає, що в однорідному магнітному полі поздовжня складова швидкості не зазнає змін. Отже, електрони з різними значеннями 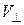 за один оберт перемістяться в поздовжньому напрямку на однакову відстань l і сфокусуються в одній точці.
за один оберт перемістяться в поздовжньому напрямку на однакову відстань l і сфокусуються в одній точці.
Як правило, для визначення відношення 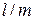 використовують осцилографічну електронно-променеву трубку, вміщену в соленоїд (рис.12.2), в якій створюється вузький пучок електронів, які мають однакову швидкість
використовують осцилографічну електронно-променеву трубку, вміщену в соленоїд (рис.12.2), в якій створюється вузький пучок електронів, які мають однакову швидкість 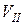 [9]. Пролітаючи між вертикально відхиляючими пластинами, під дією змінної напруги
[9]. Пролітаючи між вертикально відхиляючими пластинами, під дією змінної напруги  (подається на ці пластини від генератора Г) електрони отримують вертикальну складову швидкості
(подається на ці пластини від генератора Г) електрони отримують вертикальну складову швидкості 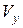 під дією прискорювальної напруги
під дією прискорювальної напруги 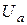 . Різні електрони матимуть різні швидкості
. Різні електрони матимуть різні швидкості 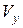 . На екрані трубки буде видно вертикальну лінію, довжина якої залежатиме від максимальної величини
. На екрані трубки буде видно вертикальну лінію, довжина якої залежатиме від максимальної величини 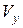 , яка в свою чергу залежатиме від амплітуди
, яка в свою чергу залежатиме від амплітуди  .
.
За допомогою соленоїда, надітого на трубку (рис.12.2), створюють спочатку слабке магнітне поле. Електрони починають рухатись у трубці вздовж гвинтової лінії, вертикальна лінія повернеться на деякий кут
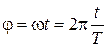 , (12.7)
, (12.7)
який залежить тільки від В (або від величини струму І в соленоїді). Зі збільшенням І кут φ зростатиме, а радіус гвинтової лінії зменшуватиметься. При деякому значенні струму 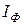 (відповідно індукції
(відповідно індукції 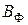 ) кут φ досягне
) кут φ досягне 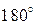 , а пряма лінія стягнеться в точку. Визначивши
, а пряма лінія стягнеться в точку. Визначивши 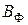 , можна обчислити
, можна обчислити 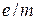 . Для цього в формулу (12.4) підставимо значення T із співвідношення (12.6), тоді отримаємо
. Для цього в формулу (12.4) підставимо значення T із співвідношення (12.6), тоді отримаємо
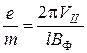 . (12.8)
. (12.8)
Індукція магнітного поля соленоїда визначається формулою
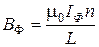 , (12.9)
, (12.9)
де 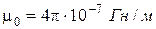 – магнітна стала;
– магнітна стала;
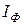 – значення струму в соленоїді, при якому відбувається фокусування електронів;
– значення струму в соленоїді, при якому відбувається фокусування електронів;
n – кількість витків соленоїда;
L – довжина соленоїда.
Підставивши значення 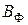 (12.9) в формулу (12.8), знайдемо робочу формулу для визначення питомого заряду електрона.
(12.9) в формулу (12.8), знайдемо робочу формулу для визначення питомого заряду електрона.
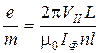 . (12.10)
. (12.10)
12.3 Опис комп’ютерної програми
Зовнішній вигляд інтерфейсу програми зображено на рис. 12.3. Програма розраховує та виводить на екран траєкторію руху електронів в магнітному полі. Рух електрона описується за допомогою модифікованого алгоритму Ейлера (додаток Б). Для управління програмою створено головну панель та три допоміжних панелі настройок.
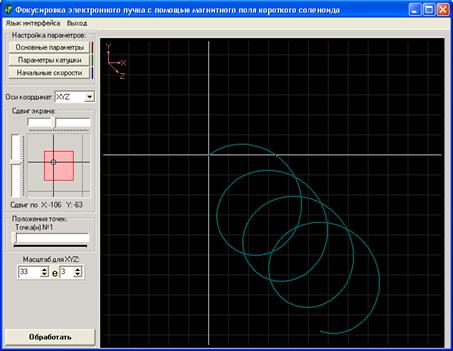
Рисунок 12.3
На головній панелі програми можна вибрати площину спостереження руху частинки: ХY, ZX, ZY або тривимірний простір – XYZ (рис.12.3). Зображення можна переміщувати вліво, вправо, вгору, вниз, змінювати його масштаб, виділяти одну частинку з групи частинок, “проганяти” її вздовж траєкторії в ручному режимі.
Перша допоміжна панель – “основні параметри”. В ній настроюються такі параметри як: маса частинки m, заряд q, крок в часі t, а також кількість кроків, які обчислюються – “візуалізовані кроки” та кількість “невидимих кроків”, які обчислюються між двома сусідніми візуалізованими.
Друга допоміжна панель – “Параметри котушки”. На ній встановлюються: радіус котушки R, кількість витків n, число N, на яке розбивається виток котушки при обчислюванні індукції B в заданій точці простору (за формулою Біо-Савара-Лапласа), довжина котушки L та сила струму в соленоїді І. Можна також встановити тип поля “однорідне” або “неоднорідне”. Для однорідного поля В обчислюється один раз. Для неоднорідного поля обчислення індукції здійснюється для кожного кроку, при цьому швидкість обчислень значно знижується.
Третя допоміжна панель – “початкові швидкості”, дає можливість вибрати кількість електронів, траєкторії яких обробляються одночасно (від одного до п’яти), та встановлювати їх початкові швидкості V.
Програма дає можливість обчислювати та спостерігати рух електронів в магнітному полі в широкому діапазоні зміни вказаних параметрів, обираючи їх так, щоб досягти фокусування електронів поздовжнім магнітним полем.
12.4 Інструкція користувачу
1. Оберіть однорідне магнітне поле. Вибираючи відповідні значення складових 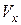 ,
, 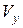 ,
,  початкової швидкості отримайте прямолінійну траєкторію для одного електрона вздовж осі Z, кругову траєкторію в площині XY.
початкової швидкості отримайте прямолінійну траєкторію для одного електрона вздовж осі Z, кругову траєкторію в площині XY.
2. Встановіть І=100A. На панелі “Основные параметры” виберіть максимальне “число шагов” – 1000 . Підберіть значення складових швидкості 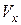 ,
, 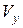 ,
,  так , щоб спостерігалася спіральна траєкторія (при цьому має бути
так , щоб спостерігалася спіральна траєкторія (при цьому має бути 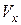 ,
, 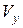 ~10
~10 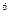 м/с,
м/с,  ~10
~10 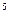 м/с). Зарисуйте та поясніть отримані криві.
м/с). Зарисуйте та поясніть отримані криві.
3. Змініть 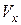 на –
на – 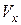 ,
, 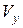 на –
на – 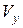 . Отримайте проекції траєкторії на площини XY, ZX, ZY ізарисуйте отримані криві. Порівняйте їх з кривими пункту 2. Поясніть причини змін.
. Отримайте проекції траєкторії на площини XY, ZX, ZY ізарисуйте отримані криві. Порівняйте їх з кривими пункту 2. Поясніть причини змін.
4. Задайте початкові швидкості 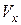 ,
, 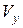 ,
,  для п’яти електронів, дані візьміть з табл. 12.1. В цій таблиці наведені величини швидкості для першої частинки. Значення
для п’яти електронів, дані візьміть з табл. 12.1. В цій таблиці наведені величини швидкості для першої частинки. Значення 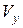 для інших чотирьох електронів підберіть так, щоб вони відрізнялись від
для інших чотирьох електронів підберіть так, щоб вони відрізнялись від 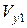 на кілька одиниць ((1..2)·105, м/с). Наприклад, для першого варіанта
на кілька одиниць ((1..2)·105, м/с). Наприклад, для першого варіанта 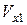 =0,
=0, 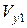 =4·105 м/с,
=4·105 м/с, 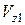 =6·106 м/с. Тоді
=6·106 м/с. Тоді 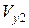 =5·105 м/с,
=5·105 м/с, 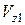 =6·106 м/с
=6·106 м/с
і т.д. Головне, щоб на екрані траєкторії п’яти частинок можна було добре розрізнити. Для всіх частинок складова швидкості 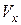 =0, складова
=0, складова  для всіх п’яти частинок – однакова.
для всіх п’яти частинок – однакова.
Змінюючи величину струму, досягніть фокусування електронів. Спостерігайте у площині XY. Щоб точніше визначити момент фокусування, скористайтесь масштабом. Якщо траєкторії виходять за межі радіуса котушки R, змініть R так, щоб електрони знаходились в середині котушки.
Таблиця 12.1 – Вихідні дані
| Номер варіанта | |||||||||||||
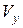 ·105, м/с ·105, м/с | |||||||||||||
 ·106, м/с ·106, м/с | |||||||||||||
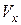 ·105, м/с ·105, м/с | |||||||||||||
| L·10-3, м | |||||||||||||
| n | |||||||||||||
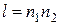 | Кількість кроків розрахунку, n1 | ||||||||||||
| Кількість невидимих кроків, n2 |
Початкове значення І=1A , кінцеве 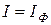 – струм фокусування – коли всі електрони зберуться в одну точку. Спостерігайте траєкторії електронів в різних площинах. За допомогою повзунка “Положение точек” при одному зі значень
– струм фокусування – коли всі електрони зберуться в одну точку. Спостерігайте траєкторії електронів в різних площинах. За допомогою повзунка “Положение точек” при одному зі значень 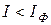 пройдіться вздовж траєкторій. Через кінцеві точки “проведіть” пряму, приклавши лінійку до екрана.
пройдіться вздовж траєкторій. Через кінцеві точки “проведіть” пряму, приклавши лінійку до екрана.
5. Визначіть значення струму 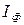 . Обчисліть значення
. Обчисліть значення 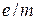 за формулою (12.10), де
за формулою (12.10), де 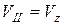 . Результати занесіть в табл. 12.2.
. Результати занесіть в табл. 12.2.
Таблиця 12.2 – Результати розрахунків
| № | 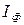 , А , А | 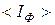 , А , А | 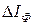 , А , А | 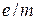 ·10-11, Кл/кг ·10-11, Кл/кг | 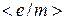 ·10-11, Кл/кг ·10-11, Кл/кг | 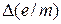 ·10-11, Кл/кг ·10-11, Кл/кг |
6. Повторіть пункти 4 і 5 ще тричі, збільшуючи 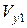 на дві одиниці
на дві одиниці
(2·105, м/с), і визначіть середнє значення 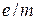 . Результати занесітьдо табл. 12.2.
. Результати занесітьдо табл. 12.2.
7. Обчисліть абсолютну похибку вимірювання 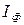 та
та 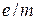 . Результати занесіть до табл. 12.2.
. Результати занесіть до табл. 12.2.
12.5 Зміст звіту
Звіт має містити: мету роботи, рисунки за пунктами 2 і 3, результати вимірювань, зведені в таблиці, похибки вимірів, висновки.
12.6 Контрольні запитання і завдання
1. Що таке сила Лоренца, коли вона виникає?
2. Проаналізуйте, як змінюється сила Лоренца в залежності від взаємної орієнтації векторів 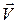 і
і 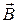 , коли вона максимальна, мінімальна.
, коли вона максимальна, мінімальна.
3. Як рухатиметься заряджена частинка в однорідному магнітному полі, коли: 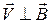 ;
; 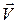 ║
║ 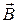 ;
; 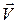 і
і 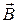 спрямовані під кутом α ?
спрямовані під кутом α ?
4. Яку установку використовують для визначення відношення заряду електрона до його маси 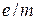 ?
?
5. Як відбувається фокусування електронів в магнітному полі?
