Законы и формулы к выполнению задач по теме №1

Кинематика

Поступательное движение

1. Уравнение движения материальной точки (или центра масс абсолютно твердого тела),

движущейся равномерно вдоль оси x: , (1.1)

движущейся равноускоренно вдоль оси x: . (1.2)

Для прямолинейного движения разность между конечной (x) и начальной (x₀) координатами тела равна пройденному пути S.

2. Закон изменения скорости при равноускоренном движении:

. (1.3)

Здесь и – скорость тела в начальный момент времени и в момент времени t соответственно, a – линейное ускорение.

3. Средняя путевая скорость:

, (1.4)

где ΔS – величина пути, пройденного телом за интервал времени Δt.

4. Тангенциальное ускорение:

. (1.5)

5. Нормальное ускорение:

, (1.6)

где R – радиус кривизны траектории.

6. Полное ускорение:

. (1.7)

Вращательное движение

7. Уравнение движения материальной точки (или центра масс абсолютно твердого тела), движущейся равноускоренно по окружности радиуса R:

. (1.8)

8. Закон изменения скорости при равноускоренном движении:

. (1.9)

Здесь Δφ – угол поворота тела за время t, ω₀ и ω – угловые скорости тела в начальный момент времени и в момент времени t соответственно, ε – угловое ускорение.

9. Угловая скорость ω связана:

с линейной скоростью 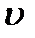: , (1.10)

с линейной частотой ν: , (1.11)

с периодом колебаний Т: . (1.12)

10. Угловое ускорение ε связано с тангенциальной составляющей линейного ускорения a_τ соотношением:

. (1.13)

11. Угловая скорость ω связана с нормальной составляющей линейного ускорения a_n соотношением:

. (1.14)

Динамика

Поступательное движение

12. Второй закон Ньютона:

. (1.15)

– геометрическая сумма сил, действующих на тело, m – масса тела.

13. Третий закон Ньютона:

, (1.16)

где – сила, действующая на первое тело со стороны второго, а – сила, действующая на второе тело со стороны первого.

14. Силы в механике:

· сила упругости , где x – величина упругой деформации тела, k – коэффициент упругости;

· сила тяжести , где – ускорение свободного падения;

· сила трения (скольжения) , где μ – коэффициент трения,

N – сила нормального давления (сила реакции опоры).

15. Импульс материальной точки (твердого тела) массой m:

. (1.17)

16. Закон сохранения импульса изолированной системы тел:

. (1.18)

17. Кинетическая энергия тела:

. (1.19)

18. Потенциальная энергия:

· упругодеформированной пружины , (1.20)

где k – жесткость пружины, x – величина деформации;

· тела, находящегося в однородном поле силы тяжести , (1.21)

где h – высота тела над уровнем, принятым за нулевой (имеется при этом в виду, что h<<R, где R – радиус Земли).

19. Закон сохранения механической энергии:

, (1.22)

где E – полная энергия изолированной системы.

20. Работа постоянной силы:

, (1.23)

где S – перемещение тела под действием силы F, α – угол между направлением силы и направлением перемещения.

21. Связь работы сил, действующих на тело, и кинетической энергии тела:

, (1.24)

где ΔE – изменение полной энергии системы под действием внешних сил.

Вращательное движение

22. Модуль момента силы относительно неподвижной точки О:

, (1.25)

где r – модуль радиус-вектора, проведенного из точки О, через которую проходит ось вращения в точку приложения силы F; α – угол между радиус-вектором и вектором силы. Направление вектора момента силы совпадает с направлением поступательного движения правового винта при его вращении от к .

23. Основной закон динамики вращательного движения:

, (1.26)

где J – момент инерции тела относительно оси вращения, – угловое ускорение.

24. Момент инерции относительно оси, проходящей через центр масс для:

·полого цилиндра (обруча) радиусом R ; (1.27)

·сплошного цилиндра (диска) радиусом R ; (1.28)

·прямого тонкого стержня длиной l ; (1.29)

·шара радиусом R . (1.30)

25. Кинетическая энергия тела, вращающегося вокруг неподвижной оси:

, (1.31)

где ω – угловая скорость.

26. Кинетическая энергия катящегося тела:

. (1.32)