Пояснение к рабочей программе
При изучении темы "Квантовая физика" надо иметь в виду следующее. Начало развития квантовой физики связано с решением немецким ученым Максом Планком проблемы излучения абсолютно черного тела. Необходимо знать гипотезу Планка о квантовании энергии осцилляторов и уяснить, что на основании формулы Планка могут быть получены законы Стефана- Больцмана и Вина (в контрольной работе это задачи 601-610).
Развитие гипотезы Планка привело к созданию представлений о квантовых свойствах света. Кванты света называются фотонами. С позиций квантовой теории света объясняется такое явление как фотоэффект. Здесь следует знать формулу Эйнштейна для фотоэффекта (задачи 611-620 контрольной работы).
Дальнейшее развитие квантовой физики связано с построением теории строения атома. О сложном строении атома говорят исследования спектров излучения разряженных газов (т.е. спектров излучения отдельных атомов). Задачи 621-630 контрольной работы посвящены изучению закономерностей в спектре атома водорода.
У студента должно сформироваться представление, что электромагнитное излучение имеет двойственную природу (корпускулярно- волновой дуализм). Корпускулярно-волновой дуализм присущ также материальным частицам. Согласно гипотезе де Бройля, движение любой частицы всегда связано волновым процессом. Определению длины волны де Бройля посвящены задачи 631-640 контрольной работы.
Изучение теоретического курса в программе завершается рассмотрением вопросов квантовой механики. Здесь важно понять, что существуют границы применимости законов классической механики, которые устанавливаются из соотношения неопределенностей Гейзенберга. Состояние микрочастицы в квантовой механике описывается волновой функцией. Важно понять статистический смысл волновой функции, т.е. понять - как определить вероятность нахождения частицы в различных точках пространства. Вид волновой функции находится из решения уравнения Шредингера. Необходимо рассмотреть применение уравнений Шредингера к стационарному состоянию частицы в прямоугольной бесконечно глубокой потенциальной яме, из которого вытекает квантование энергии (задачи 641-650). Применение уравнения Шредингера к описанию поведения электрона в водородоподобном атоме приводит к квантованию энергии и момента импульса электрона. Следует выяснить физический смысл квантовых чисел, характеризующих состояние электрона в атоме водорода.
При изучении темы "Периодическая система элементов" необходимо обратить внимание на роль принципа запрета Паули, связанного с существованием у электрона спина - фундаментальной характеристики микрочастицы. При изучении взаимосвязи между веществом и излучением важно знать, что помимо поглощения и спонтанного (самопроизвольного) излучения существует вынужденное (индуцированное) излучение. Практическое использование вынужденного излучения привело к созданию оптических квантовых генераторов (лазеров).
При изучении темы "Квантовая статистика. Зонная теория твердых тел" основное внимание должно быть уделено понятию энергетических зон в кристаллах, выяснению различий между металлами, полупроводниками и диэлектриками. Изучению проводимости полупроводников посвящены задачи 651-660 контрольной работы. Важно понять распределение электронов по энергиям (распределение Ферми-Дирака), иметь качественное представление о таких явлениях как термоэлектронная эмиссия, термоэлектрические явления и, наконец, рассмотреть примесную проводимость полупроводников и вольт-амперную характеристику р-n перехода.
Основные формулы
| Закон Стефана-Больцмана: где R - энергетическая светимость (излучательность) абсолютно черного тела, т.е. энергия, испускаемая в единицу времени с единицы площади: σ - постоянная Стефана-Больцмана: | 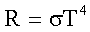 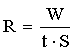 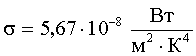 |
| Энергетическая светимость (излучательность) серого тела: где α - коэффициент черноты. | 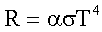 |
| Закон смещения Вина: где λm - длина волны, на которую приходится максимум энергии излучения; b - постоянная Вина : | 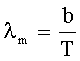 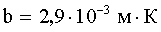 |
| Импульс фотона: где λ - длина волны; h - постоянная Планка: | 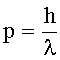 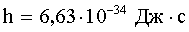 |
| Энергия фотона: где ν - частота; с - скорость света в вакууме: | 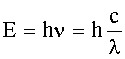 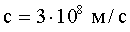 |
Формула Эйнштейна для фотоэффекта: где hν - энергия фотона, падающего на поверхность металла; А - работа выхода электрона из металла; 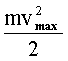 - максимальная кинетическая энергия фотоэлектрона. - максимальная кинетическая энергия фотоэлектрона. | 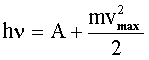 |
| Красная граница фотоэффекта: где λк - максимальная длина волны, при которой возможен фотоэффект; νк - минимальная частота, при которой возможен фотоэффект. | 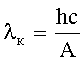 или или 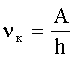 |
| Сериальные формулы спектра водородоподобного атома где R - постоянная Ридберга R=1,097·107 м-1, z - порядковый номер элемента; Серия Лаймана m=1, n=2,3,4... Серия Бальмера m=2, n=3,4,5... Серия Пашена m=3, n=4,5,6... Серия Брекета m=4, n=5,6,7... и т.д. | 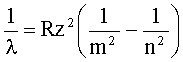 |
Длина волны де Бройля: где р - импульс частицы. В классическом приближении (при v<<c): p = mv; m - масса частицы; v - скорость частицы; с - скорость света в вакууме. В релятивистском случае (при 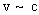 ): ): | 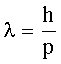 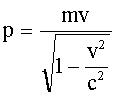 |
| Связь импульса с кинетической энергией Wк в релятивистском приближении: где E0 - энергия покоя частицы: | 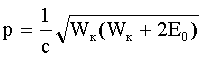 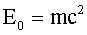 |
| Плотность вероятности нахождения частицы в соответствующем месте пространства | 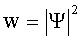 |
| Волновая функция, описывающая состояние частицы в бесконечно глубокой одномерной потенциальной яме где l - ширина ямы, х - координата частицы в яме (0 ≤ x ≤ l), n - квантовое число (n=1,2,3...). | 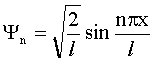 |
| Энергия частицы в бесконечно глубокой одномерной потенциальной яме где m - масса частицы. | 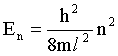 |
| Электропроводность собственных полупроводников где е - заряд электрона, n - концентрация носителей заряда, uр - подвижность электронов, un - подвижность дырок. | 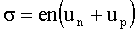 |
| Постоянная Холла для полупроводников типа алмаза, германия, кремния | 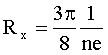 |
