Исправление однократной ошибки

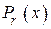Исправление одиночной ошибки связано с определением разряда, в котором произошла ошибка. Это производится на основании анализа остатков от деления многочленов ошибок на неприводимый полином . Каждому остатку соответствует один из разрядов кодовой комбинации, в которой произошла ошибка. Чем больше остатков, тем больше ошибок можно исправить. Наибольшее число остатков дает неприводимый полином 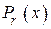, так как он не содержит ни одного сомножителя кроме самого себя.

Боузом и Чоудхури доказано[20], что существует циклический код разрядности

, (5.18)

где m = 1, 2, 3, …,

с кодовым расстоянием

. (5.19)

При этом число проверочных символов удовлетворяет соотношению

. (5.20)

Питерсеном [Коды, исправляющие ошибки] доказано, что полином вида

(5.21)

может быть представлен в виде произведения неприводимых многочленов, степени которых являются делителями числа m от 1 до m включительно [Березюк].

Соотношение между числом исправляемых ошибок s, числом информационных символов и числом проверочных символов регулируется формулой (5.6).

В таблице 5.4 приведены значения числа символов n в кодовой последовательности в зависимости от величины m, обеспечивающие кодовое расстояние d=3

Таблица 5.4
m					…
n					…
r					…
k					…

при исправлении одиночной ошибки. Для значений n = 3, 7, 15 по формуле (5.21) получены множества неприводимых многочленов

,

,

.

Не каждый многочлен даёт необходимое число остатков. Например, при исправлении однократной ошибки в 15-разрядном коде необходимо 15 остатков , полученных от деления кода ошибки на неприводимый полином. Однако, если выбран полином будет всего шесть остатков. В то же время полином даёт 15 остатков. Двоичное значение полинома 11001.

Образование циклического кода. n-разрядная кодовая комбинация имеет вид 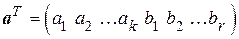, . Положим, определены k, r и n . Тогда известны неприводимый многочлен и многочлен , соответствующий k-разрядной комбинации информационных символов . Необходимо определить проверочные символы . Один из методов образования кода заключается в следующем.

Многочлен умножается на . Это соответствует приписыванию r нулей справа в кодовой последовательности . Произведение делится на неприводимый полином и получается 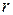- разрядный остаток . Все символы в кодовой последовательности замещаются символами остатка. В результате имеем многочлен

.

Полученный многочлен делится без остатка на неприводимый многочлен. Действительно,

,

где частное от деления , остаток отсутствует.

Если в одном из разрядов символ изменил своё значение, остаток от деления не равен нулю. Каждому ошибочному символу в кодовой комбинации соответствует свой остаток (синдром).

Пусть n = 7, k = 4, r = 3. Выберем полином 1011, который дает 7 остатков. Положим, . Неизвестными являются проверочные символы .

Определим полиномы и соответствующие им коды 1110000, 1011. Остаток от деления полинома на полином равен 100.

Заменим нули проверочной части кода 1110000 кодом остатка и получим закодированную кодовую комбинацию 1110100, которому соответствует полином вида . Разделив полином на полином , получим полином 000.

Исправление однократной ошибки. Для исправления однократных ошибок определим коды ошибок, соответствующие каждому разряду кодовой комбинации. Заменяя исправный символ в коде 1110100 ошибочным и деля полученный код на код неприводимого многочлена, получим код ошибки (синдром) для соответствующего разряда. В результате получится таблица 5.5. Если искажён символ, скажем , то после деления кода с искажённым символом на код неприводимого многочлена получим синдром 011, что позволит инвертировать символ .

Таблица 5.5
Код сообщения
Синдром S

Исправление однократной ошибки возможно несколькими методами. Используя методы исправление однократной ошибки систематическими кодами можно так же создать проверочную матрицу, а по ней записать проверочные уравнения. Другим методом является метод, основанный на свойствах записи циклических кодов и весе однократной ошибки, равный единице.

Считается, множество кодов, составляющие разрешённые комбинации , образовано с помощью выбранного неприводимого полинома и он остается неизменным во время исправления однократной ошибки. В зафиксированной кодовой комбинации содержится однократная ошибка. При делении зафиксированной кодовой комбинации на код образующего полинома получается остаток. Если все разряды кода не искажены, остаток равен нулю. Искажение одного из символов приводит к остатку, отличного от нуля. Анализ остатка позволяет определить искажённый символ. Ввиду того, что ошибка однократная и надо найти разряд, в котором произошла ошибка, то вес остатка должен быть равен единице. Чтобы проверить каждый разряд кода на наличие ошибки производится поэтапно циклический сдвиг влево на один разряд кодовой комбинации. На каждом этапе осуществляется деление сдвинутого кода на неприводимый полином и определяется вес остатка . Процедура циклических сдвигов останавливается, если вес остатка =1. Этот остаток служит индикатором того, что последний разряд в сдвинутом коде ошибочный и его надо инвертировать. Инвертирование достигается суммированием по модулю 2 сдвинутого кода с кодом остатка.

Чтобы восстановить неискажённую кодовую комбинацию производятся циклические сдвиги вправо столько раз, сколько производились циклические сдвиги влево.

Пример 5.6 Пусть n = 7, k = 4, r = 3. Выберем полином

1011, который дает 7 остатков. Выберем из множества разрешённых кодовых комбинаций код 1110100 и внесём ошибку в 4-ый разряд 1111100. На рисунке 5.8 показана процедура определения искажённого символа. Разделив кодовую комбинацию с ошибкой на неприводимый полином, убедимся, что вес остатка w

Сдвига нет Å 1111100 1011¯ Å 1011¯¯ Å     w > 1 а 1-ый сдвиг влево Å 1111001 1011¯ Å 1011¯¯ Å     w > 1 б а б в 3-ий сдвиг влево Å 1100111 1011¯ Å 1011¯ Å 1011¯     w > 1   2-ой сдвиг влево Å 1110011 1011¯ Å 1011¯¯     w > 1 в 4-ый сдвиг влево Å 1001111 1011¯¯ Å 1011¯     w = 1 д г д е Исправление ошибки Å 1001111   1001110 Рис. 5.8 Процедура определения искажённого символа

больше 1, рисунок 5.8 а. На рисунках 5.8 б, 5.8 в, 5.8 г показаны процедуры циклического сдвига и получения остатков, больших единицы. На рисунке 5.8.д демонстрируется, после очередного циклического сдвига и деления полученного кода на неприводимый полином остаток равен единице, следовательно вес остатка w=1. Это значит последний сдвинутый символ ошибочный. Чтобы исправить ошибочный символ, последнюю кодовую комбинацию сложим по модулю 2 с остатком, рисунок 5.8.е. Произведя последовательно 4 раза циклический перенос вправо кодовой комбинации с исправленным символом, получим безошибочную кодовую комбинацию:

1001110 ® 0100111, 1010011, 1101001, 1110100.

Оглавление

1. ТЕОРИЯ ИНФОРМАЦИИ1

1.1 Теорема Котельникова1

1.2 Квантование сигнала по уровню3

2. Мера информации6

2.1 Мера информации по Шеннону6

2.2 Энтропия дискретного ансамбля сообщений8

2.4 Энтропия непрерывного ограниченного ансамбля12

2.3 Количество взаимной информации14

2.3.1 Дискретный канал передачи информации14

2.3.2 Непрерывный канал передачи информации17

2.3.3 Эпсилон-энтропия (ε-энтропия)20

3. Кодирование источника информации22

3.1 Метод кодирования равномерным кодом23

3.2 Метод кодирования Шеннона-Фано27

3.3 Метод кодирования Хафмана30

3.4 Теорема оптимального кодирования источника32

независимых сообщений.32

4 Канал связи35

4.1 Скорость передачи информации и37

пропускная способность канала связи37

4.2 Канал без шумов39

4.3 Канал с шумами41

4.4 Непрерывный канал связи43

4.5 Теорема Шеннона о пропускной способности47

частотно ограниченного канала47