Знак равенства будет в том случае, когда значения сигнала распределены по нормальному закону

Согласно определению пропускной способности

(4.34)

Энтропия 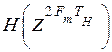- это энтропия множества отсчетов в моменты времени 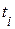с интервалом 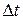из ансамбля 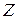для всех моментов времени 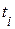. Ввиду того, что неизвестны вероятностные характеристик процесса 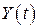, справедливы выражения

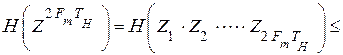
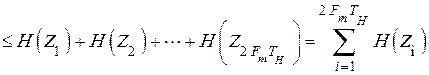. (4.35)

. (4.36)

.

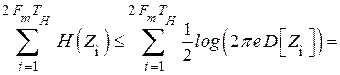
Используем свойство: среднегеометрическое не превышает среднеарифметическое. Тогда

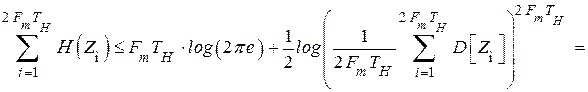
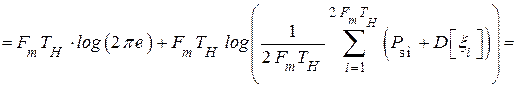
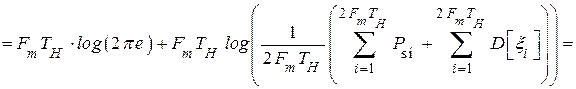
(4.37)

При вычислении условной энтропии используется независимость символов попарно на входе и выходе канала связи.

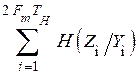= (4.38)

Условная энтропия 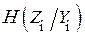зависит от шума и распределена по нормальному закону (ссылка на канал связи ****) согласно условиям теоремы. Энтропия случайной величины, распределённой по нормальному закону, равна

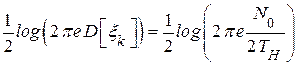. (4.39)

После подстановки (**.5) в (**.14) получим

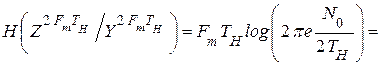
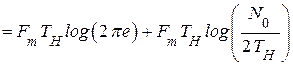(4.40)

Подставим выражения (**.13) и (**.16) в (**.10):

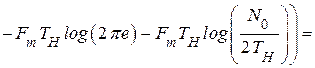
В результате получим

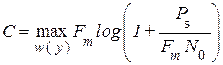(4.41)

Если сигнал на входе канала связи распределён по нормальному закону, пропускная способность канала равна

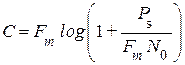(4.42)

Как видно из формулы, пропускная способность канала зависит от полосы частот, занимаемой сигналом, мощности сигнала и спектральной плотности мощности «белого» шума.

Кодирование в канале

Ранее были определены операции кодирования источников сообщений. Если полученную последовательность сигналов передавать через канал потребителю, то часть сигналов может быть искажена. Чтобы обнаружить и исправить искажения вводится некоторая избыточность информации в передаваемые кодовые комбинации. Процедура введения избыточности в кодовые комбинации называется помехоустойчивым кодированием или кодированием в канале и выполняется кодером канала. Коды, позволяющие исправлять ошибки, называются корректирующими.

Для восстановления первоначального кода служит декодер канала. На рисунке 5.1 приведена модель передачи информации с применением кодера и декодера канала.

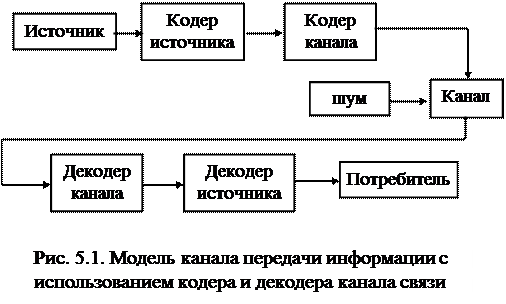Помехи могут исказить символов в кодовом слове. Если искаженные символы независимы и вероятность искажения одного символа равна , то вероятность ошибки кратности равна

, (5.1)

где 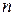- число двоичных символов в передаваемой кодовой комбинации.

Обычно 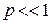. Из приведённой формулы видно, что наиболее вероятны одиночные ошибки и ошибки малой кратности. Поэтому разрабатывались корректирующие коды, определяющие одиночные ошибки и ошибки кратности 2, 3, 4.

При декодировании принятой кодовой комбинации возникают две проблемы:

- обнаружение ошибки,

- исправление ошибки.

Естественно, что вторая задача включает первую, но они различаются по методам обработки кодовой последовательности и по числу символов, необходимых для обнаружения и исправления ошибок.

Пусть на вход кодера канала поступают 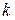- разрядные кодовые комбинации и можно образовать 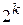- кодовых комбинаций. На выходе кодера канала получаем 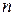- разрядные кодовые комбинации, которые образуют - кодовых комбинаций, ,и они передаются в канал связи. В множестве кодовых комбинаций содержится 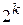кодовых комбинаций, которые соответствуют кодовым комбинациям на входе кодера канала. Назовём их разрешёнными кодовыми комбинациями, остальные - - 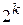запрещенными (неразрешёнными) кодовыми комбинациями.

Ошибка при декодировании обнаруживается, если декодируемый код попадет в область неразрешённых кодовых комбинаций, рисунок 5.2.

В результате передачи информации на выходе канала связи возможны различные комбинации кодов на входе кодера канала и на выходе канала связи. Их число равно 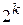. В число этих комбинаций входят:

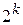- число безошибочных переходов (безошибочного декодирования),

- число переходов в другие (ошибочные) разрешённые кодовые комбинации,

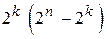- число переходов в неразрешённые кодовые комбинации. Всего различных вариантов кодовых комбинаций будет

+ + = .

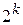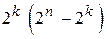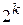
Те кодовые комбинации из 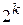разрешённых, которые перешли в область запрещённых кодовых комбинаций, могут быть обнаружены безошибочно.

Доля обнаруженных ошибочных кодовых комбинаций по отношению к общему числу вариантов приема сигналов равна

.

Рассмотрим возможность исправления ошибок. Разобьем все неразрешённые кодовые комбинации на 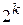подмножеств. Сопоставим каждому разрешённому коду одно определённое подмножество из области запрещённых кодов. В этом подмножестве должны содержаться коды, указывающие ошибки в принятой кодовой комбинации. Организация этих подмножеств зависит от числа исправляемых ошибок и методов кодирования-декодирования. Доля исправляемых ошибок по отношению к общему числу обнаруживаемых ошибок равна

.

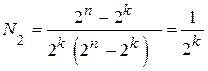Если рассмотреть геометрическую интерпретацию кодов, то кодовые комбинации будут представлять вершины 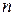-мерного куба.

Мерой различия двух кодовых комбинаций является кодовое расстояние 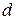, равное числу символов, которыми отличаются две кодовые комбинации, и названное расстоянием Хемминга. С геометрической точки зрения кодовое расстояние – это число рёбер многомерного куба, которое необходимо пройти от одной кодовой комбинации к другой.

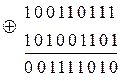Пример 5.1. Чтобы найти расстояние Хемминга между двумя кодами необходимо сложить по модулю два обе кодовые комбинации. Число «1» в результате суммирования равно кодовому расстоянию. В приведённом примере 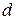=5.

Другим параметром, характеризующим кодовую комбинацию является вес кода – P - число«1» в кодовой комбинации.

Рассмотрим, как влияет кодовое расстояние на обнаружение и исправление ошибок. Положим, d = 1, т.е. все кодовые комбинации являются разрешёнными кодовыми комбинациями. Любая ошибка трансформирует одну кодовую комбинацию в другую.

Увеличим кодовое расстояние на единицу. Если расстояние между кодовыми комбинациями равно 2, то существуют запрещённые кодовые комбинации, т.е. при однократной ошибке, чтобы перейти из одной вершины гиперкуба к другой, на которой расположены разрешённые коды, нужно пройти по двум рёбрам. Но между двумя разрешёнными кодами на вершинах гиперкуба обязательно находится запрещённая кодовая комбинация. И любая однократная ошибка приводит к запрещённой кодовой комбинации, которая обнаруживается декодером.

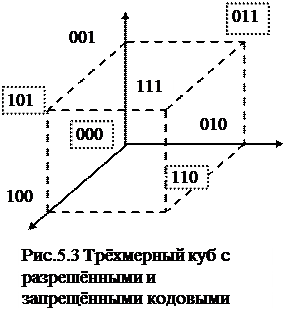На рисунке 5.3 изображён трёхмерный куб, на вершинах которого размещены трёхразрядные коды. Разрешёнными кодами являются 000, 011, 101, 110. Остальные коды 001, 010, 100, 111 ‑ запрещённые. Следует обратить внимание:

-‑ минимальное кодовое расстояние для обнаружения одиночной ошибки равно 2,

-‑ число «1» в неразрешённых кодовых комбинациях – нечётное. Поэтому иногда процедуру обнаружения одиночной ошибки называют проверкой на чётность.

В общем случае для обнаружения q кратной ошибки минимальное кодовое расстояние должно удовлетворять неравенству

(5.2)

Для исправления ошибок число проверочных кодов должно быть больше, так как проверяется каждый символ в разрешённой кодовой комбинации на наличие ошибки.

В общем случае для исправления ошибок кратности 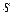минимальное кодовое расстояние меду разрешёнными кодовыми комбинациями должно удовлетворять соотношение

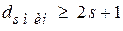(5.3)

Например, если необходимо передать символы «0» и «1» с учётом исправления возникших ошибок, то согласно неравенству (5.3), надо использовать коды с минимальным кодовым расстоянием, равным 3. Наиболее наглядным является использование кодов 000 и 111 для передачи символов «0» и «1», (рисунок 5.4).

В трёхразрядном коде две кодовые комбинации (000, 111) являются разрешёнными. Остальные кодовые комбинации – запрещенные. При наличии однократной ошибки в кодах 000 или 111 декодер обнаруживает их и исправляет.

С точки зрения геометрической интерпретации 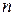-разрядный двоичный код расположен на вершинах 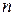-мерного куба, представляющих как разрешённые, так и запрещённые кодовые комбинации. Если интерпретировать число исправляемых символов 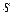как радиус 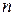-мерной сферы, из неравенства (5.3) можно получить условие

,

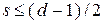определяющее подмножество разрешённых комбинаций, находящихся в 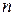-мерной сфере радиуса 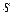, с кодовым расстоянием, не превышающим .

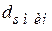Для обнаружения всех ошибок кратности и исправления ошибок кратности 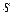расстояние между разрешёнными кодовыми комбинациями должно выбираться из условия

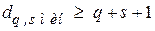. (5.4)

Приведённые формулы получены для исправления независимых ошибок. Они дают завышенные значения минимального кодового расстояния при помехе, коррелированной с сигналом.

Если длительность помехи превышает длительность сигнала, то ошибка возникает подряд в нескольких разрядах передаваемого кода. Ошибки подобного рода называются пачками или пакетами ошибок.

Длиной пачки ошибок называется число, следующих друг за другом символов, левее и правее которых в кодовой комбинации искажённых символов не содержится.

Одной из характеристик корректирующего кода является избыточность кода

, (5.5)

где 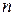‑ число символов на выходе кодера канала,

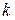‑ число символов на входе кодера канала,

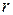- число дополнительных символов, используемых для обнаружения и исправления ошибок.

Определим связь между числом исправляемых символов и длиной 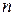разрядного кода для независимых ошибок. Общее число различных исправляемых ошибок для каждой разрешённой комбинации равно 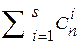,[Темников, стр. 136]. Каждая из возможных ошибок должна приводить к запрещённой кодовой комбинации, относящейся к подмножеству данной разрешённой комбинации. Таким образом, число кодов, включая разрешённую кодовую комбинацию, будет 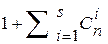. Ввиду того, что общее число различных комбинаций 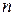-разрядного кода составляет , число разрешённых комбинаций ‑ 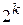, то должно выполняться неравенство

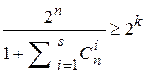. (5.6)

Эта граница была найдена Хеммингом, [**]. Из неравенства (5.6) можно определить число символов 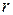, необходимых для исправления не более, чем кратных ошибок:

. (5.7)

Приведенные формулы позволяют оценивать возможности метода кодирования при заданных ограничениях на число символов в кодовой комбинации.

Систематические коды

Для передачи информации используются разнообразные методы кодирования, зависящие от требований к восстанавливаемой информации, а также от свойств линий передачи информации. На рисунке 5.5 приведена сокращённая таблица кодов, взятая из [Березюк Кодирование информации]. В левой части таблицы указаны коды, применяемые для кодирования источников сообщений. В правой части таблицы указаны коды, применяемые для помехоустойчивого кодирования. Избыточные коды помимо информационных символов содержат дополнительные символы, применяемые для обнаружения и исправления ошибок. Сами избыточные коды делятся на блочные и непрерывные. Непрерывные коды характерны тем, что между символами, несущими информацию, находятся проверочные символы, т.е. на вход кодера канала подаётся последовательность информационных символов. На выходе кодера получается новая последовательность символов, перемежающихся с проверочными символами. Процесс кодирования, передачи информации и декодирования производится в непрерывном режиме .

При блочном кодировании информации производится объединение передаваемых сообщений в блоки, и они затем подвергаются кодированию. Блок состоит из 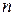символов, из которых 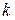символов являются информационными, 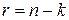- проверочными. В блочных кодах выделяются разделимые коды. В них 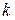известных позиций отводятся под информационные символы, а остальные 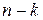позиций – под передачу проверочных символов. В неразделимых кодах такого чёткого разграничения нет. Разделимые коды обозначаются как . Разделимые коды в свою очередь делятся на систематические и несистематические коды.

Систематические 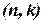коды – это коды, в которых проверочные символы представляют линейную комбинацию информационных символов. Часто эти коды называют линейными кодами.

Пусть 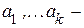информационные символы,

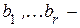проверочные символы,

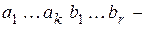разрешённая кодовая комбинация.

Согласно определению систематического кода каждый символ 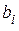может быть записан как линейная комбинация информационных символов.

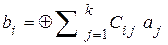, (5.8)

где коэффициенты 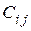принимаю значения 0 или 1.

Положим, новая разрешённая комбинация. Составим сумму по модулю два двух проверочных символов для одних и тех позиций прежней и новой кодовых комбинаций

.

Как видно из полученного выражения, вновь полученный проверочный символ на 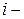ой позиции является линейной комбинацией информационных символов.

Сумма по модулю два разрешённых кодовых комбинаций дает также разрешённую кодовую комбинацию.