Приклади розв'язування задач
Механіка
Задача 1.Лiтак летить горизонтально на висотi 1500 м зi швидкiстю 200 м/с. Iз гармати роблять пострiл по лiтаку у ту саму мить, коли він знаходиться над гарматою. Нехтуючи опором повiтря, знайти, пiд яким кутом до горизонту має бути зроблений пострiл, щоб влучити в лiтак. Початкова швидкiсть снаряду 100 м/с.
Розв'язок
| h = 1500 м v0 = 100 м/с v = 200 м/c g = 9,8 м/с2 | Вважатимемо, що гармата знаходиться на початку координат. Рух снаряду можна розкласти на горизонтальний - рiвнoмipний i вертикальний - рiвнозмiнний рух , якi описуються рiвняннями:  (1) (1) |
| a, t - ? |
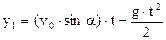 , (2)
, (2)
а рух лiтака - вiдповiдно рiвняннями:
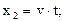 (З)
(З)
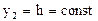 . (4)
. (4)
У мить влучання снаряду в лiтак координати цих тiл спiвпадають:
 i
i 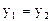 .
.
Прирiвнюючи частини, що праворуч рiвнянь (1) i (3), а також (2) i (4), одержимо
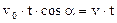 ; (5)
; (5)
 . (6)
. (6)
Із рiвняння (5) знаходимо:
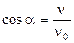 , або
, або 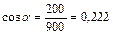 .
.
Кут, пiд яким треба зробити пострiл, дорiвнює 77 °.
Для визначення часу польоту снаряда до влучання в цiль перепише-мо рiвняння (6)
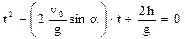 .
.
Розв'язання цього (квадратного) рiвняння
 .
.
Визначимо розмiрнiсть шуканого часу за знайденим спiввiдношенням:
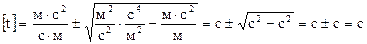 .
.
Розмiрнiсть є вiдповідною . Знайдемо числове значення t:

Отже, маємо два значения: t1 = 177 c i t2 = 1,6 с.
Два значення t зумовлено можливiстю влучання в лiтак під час руху снаряду при підійманні (t2) i при його опусканнi (t1) пiсля проходження через найвищу точку траєкторiї.
Задача 2. Колесо радiусом 0,1 м обертається так, що залежнiсть кута повороту радiусу вiд часу описується рiвнянням j = А + В×t + С×t3 , де А = 4 рад; В = 1,4 рад/с i С = 5 рад/с2. Знайти тангенцiальне, нормальне i повне прискорення точок на ободi колеса в момент t = 0,2 с.
Розв'язок
| R = 0,1 м j = А+В×t+С×t3 А = 4 рад В = 1,4 рад/с С = 5 рад/с3 t = 0,2 с | Знайдемо залежнiсть вiд часу кутової швидкостi : 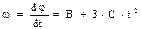 . (1) Для кутового прискорення одержуємо . (1) Для кутового прискорення одержуємо 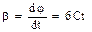 (2) Згiдно з формулами (1) , (2) і умовою задачi шуканi розмiрностi дорівнюють: (2) Згiдно з формулами (1) , (2) і умовою задачi шуканi розмiрностi дорівнюють: |
| ат , аn , а - ? |
[ω] = рад/с + (рад×с2)/с3 = рад/с + рад/с = рад/с,
[ß] = (рад×с)/с3 = рад/с2.
Числовi значення w i β, згiдно (1) i (2) , дорiвнюють
ω = 1,4 + 1,5 . 0,04 = 2,0 рад/с , β = 6,5.0,2 = 6,0 рад/с2.
Визначаємо тангенцiальне ат , нормальне аn i повне а прискорення:
аn = ω2.R = (2,0)2. 0,1 = 0,4 м/с2 ;
ат = β.R = 6,0 . 0,1 = 0,6 м/с;
 .
.
Задача 3. До нитки причеплений вантаж масою 1 кг. Знайти натяг нитки, якщо iї пiдіймати з прискоренням 5 м/с2 або опускати з тим же прискоренням.
Розв'язок
| m = 1 кг g = 9,81 м/с2 а = 5 м/с2 | 1. На вантаж дiють сили: вниз - сила тяжiння m×g, вгору - сила натягу нитки F1. Рiвнодiюча цих сил, F1 – m×g, надає вантажу прискорення, яке спрямоване в бiк F1. Застосовуючи другий закон Ньютона, запишемо: |
| F1, F2 – ? |
m×а = F1 - m×g ,
звiдки знаходимо силу натягу нитки: F1 = m ( g + a ).
Розмiрнiсть - [ F] = кг× ( м/с2 + м/с2 ) = H.
Чисельно - F1 = 1×( 9,81+5 ) = 14,81 Н.
2.На вантаж, що опускається, дiє вниз сила тяжiння m×g i вгору -сила натягу нитки F2. Тiло має прискорення, спрямоване в бiк m×g, тому за другим законом Ньютона рiвнодiюча двох протилежно спрямованих сил має дорiвнювати m×a:
m×a = m×g - F2 ,
F2 = m ( g – a ).
Розмiрнiсть - [ F2 ] = кг× ( м/с2 – м/с2 ) = Н.
Чисельно - F2 = 1×( 9,81 – 5 ) = 4,81 H.
Задача 4. Двi гирi 2 кг i 1 кг з'єднанi ниткою, перекинутою через невагомий блок. Знайти прискорення , з яким рухаються гирi , i натяг нитки. Тертям знехтувати.
Розв'язок
| g = 9,81 м/с2 m1 = 1 кг m2 = 2 кг | Сила натягу нитки перешкоджує її розтягненню, тому на кожний вантаж сила натягу дiє вертикально вгору. Отже, на перше тiло дiють: сила натягу нитки F1 |
| a, F – ? |
– вгору i сила тяжiння m1×g – вниз; на друге тiло дiють: сила натягу нитки F2 – вгору i сила m2×g – вниз.
Оскiльки блок “невагомий”, то - F1 = F2 = F.
Нехай тягар m1 опускається з деяким прискоренням (а це, звичай-но, неприродно), тодi тягар m2 пiдiймається з таким же прискоренням.
Згiдно з другим законом Ньютона
m1× а = m1× g – F1 , m2 ×a = F2 –m2×g ,
або, враховуючи F1 = F2 = F, перепишемо останню систему у виглядi
m1× а = m1× g – F , m2× a = F – m2×g .
Розв'язуючи систему рiвнянь, знаходимо:
a = ( m1 – m2 ) / ( m1 + m2 ) × g , F = ( 2×m1× m2 ) / ( m1 + m2 ).g.
Аналiзуючи розв'язок, робимо висновок: оскільки m1 < m2, то
а < 0 i спрямоване протилежно g, тобто попереднє припущення про те, що тягар m1 опускається з прискоренням, спрямованим вниз, неправильне i треба вважати, що m1 пiдiймається вгору з прискоренням а.
Розмiрностi: [а] = ( кг/кг ) × м/с2 = м/с2 ; [F] = ( кг2/кг ) ×м/с2 = Н.
Чисельно: а = –9,81/3 = – З,27 м/с2, F = (4/3) ×9,81 = 13,08 Н.
Зауважимо, що на вiсь блока дiє сила , що дорiвнює сумi сил:
F1 + F2 = 2×F = 26,16 Н.
Задача 5. Який перерiз матиме стальний трос при п'ятиразовому запасi мiцностi, щоб ним можна було пiдiймати вантаж масою 103кг з прискоренням 1,2 м/с2, якщо межа мiцностi сталi 7×108 Н/м2 ?
Розв'язок
| а = 1,2 м/с2 σm=7×108Н/м2 n = 5 g = 9,81м/с2 | Згiдно з другим законом Ньютона, вантаж прискорюється рiзницею мiж силою натягу троса i силою тяжiння вантажу : m×a = F - m×g , де F - необхiдна сила натягу троса. З урахуванням |
| S-? |
коефiцiєнту запасу мiцностi розрахункова сила натягу має бути в 5 разiв бiльшою: F`= 5×F.
Пружнє напруження у тросi σ =F`/S ,
Iз записаних спiввiдношень одержуємо
S = n× m× ( g – а ) / σ.
За останньою розрахунковою формулою розмiрнiсть шуканої площi S:
[S] = кг×м×м2 / ( с2 Н ) = Н× м2 / Н = м2.
Числове значення площi перерiзу троса
S = 5.103× ( 1,2 + 9,8 ) / ( 7 .108 ) = 7,9 .10-5 м2.
Задача 6.З якою швидкістю рухався вагон масою 20 т, якщо при ударi об стiну кожен з буферiв стиснувся на 10 см? Вiдомо, що пружина кожного з буферiв стискується на 1 см пiд дiєю сили 9,8.103 Н.
Розв'язок
| m = 20 т = 2×104 кг х = 10 см = 0,1 м х1 = 1 см = 0,01 м F1 = 9,8.103 Н | На підставі закону збереження енергiї можна дійти висновку, що кiнетична енергiя вагону перетворюється в потенцiальну енергiю двох стиснених пружин: Wk = 2×Wp . (1) |
| V – ? |
Вiдомо, що Wk = m×v2/2 , Wp = k×x2/2 , де m i v – маса i швидкiстьвагона;k - жорсткiсть пружини буфера; х - величина стиснення пружини. Жорсткiсть пружини k можна визначити iз спiввiдношення F1 = k × x1,
де F1 - сила, яка викликає пружну деформацiю х1. Пiдставляючи в рівняння (1) значення Wk, Wp i k , маємо
m × v2 /2 = ( F1 / x1 ) × x2,
звiдки одержуємо розрахункову формулу 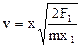 .
.
Розрахуємо розмiрнiсть [v] = м  = м
= м  = м/с.
= м/с.
Числове значення - v = 0,1  = 0,99 м/с.
= 0,99 м/с.
Задача 7. З якою швидкiстю падають на землю метеори з дуже вiд-далених областей Всесвiту, якщо їх початковi швидкостi вiдносно Землi дорiвнюють нулю. Опором повiтря знехтувати.
Розв'язок
| r1 = ¥ g = 9,81 м/с2 r2 = R = 6,67.107 м | Виходячи з закону збереження енергii, можна дійти висновку, що енергiя метеору на безмежностi має дорівнювати його енергiї на поверхнi Землi, на безмежностi потенцiальна енергiя взаємодiї метеору з Землею |
| v – ? |
Wp = – G × Mз ×m / r1
дорiвнює нулю, кінетична енергія також дорівнює нулю, тому що швидкiсть його вiдносно 3емлi дорiвнює нулю. Отже, згідно з законом збереження енергії, на поверхнi 3емлi повна енергiя метеору також дорiвнює нулю - m × v2 /2 – G × Mз × m / r2 = 0 .
Таким чином, швидкiсть метеору біля поверхнi 3емлi
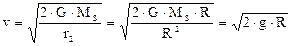 ,
,
де R – радiус земної кулi; g = G×Мз/R2 – прискорення вiльного падiння тiл бiля поверхнi Землi. Знайдемо розмiрнiсть швидкостi за розрахунковою формулою [v] =  = м /с.
= м /с.
Числове значення v = 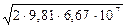 = 11,4. 103 м /с.
= 11,4. 103 м /с.
Задача 8. Маховик у виглядi диска масою 50 кг i радiусом 20 см розкручено до 480 об/хв i залишено. Пiд впливом сил тертя маховик зупинився. Знайти момент сил тертя, вважаючи його сталим, якщо до повної зупинки маховик зробив 200 обертiв.
Розв'язок
| m = 50 кг r = 20 см = 0,2 м υ = 480 об/хв = 8 об/c ω = 2×π×υ = 16×π N = 200 | Робота подолання сил тертя виконується за рахунок кiнетичної енергiї маховика : А = (I × ω2 ) / 2 , (1) де ω – кутова швидкiсть маховика; I – момент iнерцiї маховика. Робота при |
| M – ? |
обертальному русi (коли М = const)
А = М. φ, (2)
де φ – кут повороту (у радiанах – φ = 2×π×N ); М – момент дiючих сил тертя. Пiдставляючи виписанi спiввiдношення в формулу (1), одержимо
(I × ω2 ) / 2 = М. 2×π×N. (3)
Пiдставимо в рівняння (3) момент iнерцiї диску вiдносно осi обертання I, тодi одержимо розрахункову формулу
М = m×r2 ω2 / ( 8×π×N ). (4)
Розрахуємо розмiрнiсть моменту сил за формулою (4) :
[ M ] = ( кг × м2 × рад2 ) / ( рад × с2 ) = Н × м .
Зауважимо, що момент сили має розмiрнiсть Дж, але для того, щоб було очевидно, що йдеться про момент сили, а не енергетичну величину, пишуть Н × м.
Числове значення –
М = (50× 0,22 .4×.π×.4802) / ( 8×.π .200. 60 .60 ) = 1,00 Н×м.
Задача 9. Знайти рiвняння гармонiчного коливального руху , якщо максимальне прискорення точки дорiвнює 49,3 см/с2, перiод коливань 2 с i змiщення точки з положення рiвноваги в початковий момент 2,5 см.
Розв'язок
| аmax = 0,493 м / c2 Т = 2 с x0 = 2,5 .10-2 м | Рiвняння гармонічного коливання має вигляд х = А. cos ( 2..π. t / T + φ0 ), де х – змiщення точки з положення рiвноваги; А – амплiтуда; Т – перiод; t – час; |
| х = f(t) – ? |
φ0 – початкова фаза. коливання.
Прискорення точки –
а = d ( dx / dt ) / dt = – ( 4.A. π2 ) / ( T2 ) cos ( 2. π. t/ T + φ0 ).
Максимальним значення прискорення буде тоді, коли значення косинуса дорiвнюватиме – 1 , тому
аmax = 4 . А. π2 / Т2 ,
звiдки числове значення аmax = 0,05 м. Тодi рiвняння руху (1) матиме вигляд – х = 0,05 . соs ( ω. t + φ0 ), де – ω = 2.π / Т = π ( рад/с ).
Початкове значення фази знайдемо за вiдомим значенням х для t = 0: х (0) = х0.
Одержуємо соs(φ0) = 0,5 , тобто φ0 = π/3.
Остаточне рiвняння гармонiчного коливання буде мати вигляд
х =0,05 cos ( π.t + π/3 ) (м).
Молекулярна фiзика i термодинамiка
Задача 1. По газопроводу тече вуглекислий газ під тиском 4,9×105 Па i температурi 270 К. Яка швидкiсть течiї газу по трубi , якщо за 5 хв через поперечний перерiз площею 6 см2 протiкає 2,5 кг СО2?
Розв'язок
| р = 4,9×105 Па Т = 290 К t = 300 с S = 6×10-4 м2 m = 2,5 кг μ(CO2) = 0,044 кг/моль R = 8,314 Дж/(моль×К) | Якщо газ тече зi швидкiстю v, то за час t через площу S протiкає об'єм газу V = v×S×t. (1) Якщо густина газу ρ, то маса газу, що протекла, m = ρ×V = ρ×v×S×t . (2) Густину газу знайдемо за рiвнянням Менделєєва-Клапейрона: |
| V - ? |
Р×V = ( m / μ ) R×Т => ρ = m / V = ( Р×μ ) / ( R×T ) i пiдставимо iї в формулу (2):
m = P×μ / ( R×T ) ×v×S×t ,
звiдки v = ( m×R×T ) / ( P×μ× S×t ).
Знайдемо розмiрнiсть v за останньою формулою:
[v] = ( кг×Дж×К×моль ) / ( моль×К×Па×кг×м2×с ) =
Дж / ( Па× м2× с ) = м/с.
Числове значення –
v = ( 2,5×8,314×290 ) / ( 4,9×105×0,044×6×10-4×300 ) = 1,55 м /с.
Задача 2. Скiльки молекул кисню в посудинi об'ємом 100 см3, якщо при середнiй квадратичнiй швидкостi 400 м/с газ створює на стiнки тиск 9,81×103 Па.
Розв'язок
| NA= 6,02×1023 1/моль V = 10-4 м3 Р = 9,81×103 Па m = 0,032 кг/моль v = 400 м/с | Перетворимо рiвняння Менделєєва- Клапейрона до вигляду Р×V = γ×R×Т, (1) де γ - кiлькiсть молей газу, що міститься в об'ємi V. Унiверсальну газову сталу представимо у виглядi добутку сталої Больцмана k на число Авогадро NA – R = k×NA . |
| N - ? |
Загальне число молекул в об'ємi V
N = γ×.NА.
Тодi рівняння (1) приймає вигляд Р×V = N×k×Т, звiдки
N = ( Р×V ) / ( k×Т ). (2)
Знайдемо температуру газу за вiдомою середньою квадратичною швидкiстю молекул:
v2 = ( 3×R×Т ) /μ => Т = ( μ×v2 ) / ( 3×R )
i пiдставимо в формулу (2): N = ( 3×P×V×R ) / ( k×μ×v2 ) ,
де зроблена зворотня замiна R / k = NА.
Знайдемо розмiрнiсть N за розрахунковою формулою
[N] = ( Па× м3× моль×с4 ) / ( моль×кг×м2 ) = ( Дж×с4 ) / ( кг×м2 ) = [1]
– безрозмiрне.
Числове значення N -
N = (9,81×103× 10-4×6,02×1023) / (0,032×16×104) = 1,15×1020.
Задача 3. Яка кiлькiсть теплоти втрачається щогодини за рахунок теплопровiдностi повiтря мiж рамами вiкна при площi 4 м2, вiдстанi мiж рамами 30 см i нормальному атмосферному тиску? Температура повiтря в примiщеннi 291 К, зовнi - 253 К. При розрахунках вважати, що дiаметр молекул повiтря 0,3 нм.
Розв'язок
| Dt = 3600 c S = 4 м2 x = 0,3 м T1 = 291 K T2 = 253 K d = 3×10-10 м p = 1,01×105 Па μ = 0,029 κг/моль i = 5 k = 1,38×10-23 Дж/К NA= 6,02×1023 1/моль R = 8,314 Дж/(моль.К) | Кiлькiсть тепла, перенесеного внаслiдок теплопровiдностi, визначається за законом Фур'є: DQ = -æ×( dT / dx )×S×Dt . (1) Коефiцiєнт теплопровiдностi газу æ = (1/3) l <v> c×ρ, (2) де l - середня довжина вiльного пробiгу молекул; l =  . (3) Число молекул в одиницi об'єму визначається рiвнянням стану iдеального газу: p = n×k×T. (4) Величина <v> в формулі (2) - середня швидкiсть молекул газу: <v> = . (3) Число молекул в одиницi об'єму визначається рiвнянням стану iдеального газу: p = n×k×T. (4) Величина <v> в формулі (2) - середня швидкiсть молекул газу: <v> = 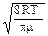 . (5) . (5) |
| DQ - ? |
Питома теплоємнiсть газу с визначається числом ступенів вiльностей (i) руху молекул газу:
с =  , (6)
, (6)
де μ - молярна маса газу.
Густину повiтря визначимо за законом Менделєєва-Клапейрона:
ρ = ( p×μ ) / ( R×T ). (7)
Пiдставимо величини (2) - (7) в рівняння (1) i одержимо, що
DQ = 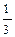
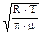
 . (8)
. (8)
Для температури повiтря вiзьмемо значення
Т = ( Т1 + Т2 ) / 2 = 272 К.
Визначимо розмiрнiсть DQ за формулою (8):
[DQ] =  ×(Дж/(К×м2))×(К/м)×м2×с = (м /с)× Дж×(с/м) = Дж.
×(Дж/(К×м2))×(К/м)×м2×с = (м /с)× Дж×(с/м) = Дж.
Числове значення -
DQ= 
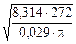
 ×
×  =2,37.104Дж=23,7 кДж.
=2,37.104Дж=23,7 кДж.
Задача 4. Яку кiлькiсть теплоти поглинає 2000 г водню, нагрiваючись вiд 273 К до 373 К при сталому тиску? Який прирiст внутрiшньої енергiї газу? Яку роботу здiйснює газ?
Розв'язок
| m = 0,2 кг DT =100 K р = соnst μ = 0,002 кг / моль i = 5 R = 8,314 Дж / (моль×К) | Кiлькiсть теплоти , яка поглинається газом, визначається за формулою: Q = 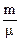 × Cp ×DT = × Cp ×DT = 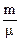 × × 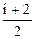 ×R×DT, (1) де m - молярна маса; i - число ступенів вiльностi; Ср - молярна теплоємнiсть газу при сталому тиску. Прирiст внутрiшньої ×R×DT, (1) де m - молярна маса; i - число ступенів вiльностi; Ср - молярна теплоємнiсть газу при сталому тиску. Прирiст внутрiшньої |
| Q , DW , A - ? |
енергiї визначається спiввідношенням
DW =  × CV × DT, (2)
× CV × DT, (2)
де CV - молярна теплоємнiсть газу при сталому об'ємi. Роботу, здiйснювану газом, визначимо, користуючись першим началом термодинамiки:
Q = DW + A, (3)
де А - робота газу.
Пiдставляючи значення величин в формули (1) – (3) , знаходимо:
[Q] = (кг.моль) / кг ×Дж / (моль×К) ×К = Дж;
[DW] = (кг×моль) / кг× Дж / (моль×К) ×К = Дж;
[А] = [ Q - DW ] = Дж.
Чисельно - Q = 0,2/0,002×7/2×8,314×100 = 290 кДж;
DW = 207 кДж; А = 83 кДж.
Задача 5. Газ, який займав об'єм 20 л пiд тиском 1,013×106 Па, iзобарично нагрiто вiд 323 К до 473 К. Знайти роботу розширення газу .
Розв'язок
| р = 1,013×10 6 Па Т1 = 323 К Т2 = 473 К V1 = 2×10-2 м3 | Робота газу А в iзобаричному процесi виражається спiввiдношенням А= р×DV, (1) де р - тиск газу; DV- змiна об'єму газу. Запишемо рівняння Менделєєва-Клапейрона для двох станiв газу при Т1 i Т2 i при р=соnst : |
| А - ? |
р×V1 =  × R×T1 , (2)
× R×T1 , (2)
p×V2 =  ×R×T2. (3)
×R×T2. (3)
Роздiлимо рівняння (3) на рівняння (2): 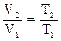 ,
,
вiднiмемо по одиницi лiворуч i праворуч:
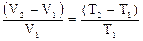
та визначимо змiну об'єму DV=V2-V1:
DV = [ ( T2 - T1 ) / T1 ] × V1.
Пiсля пiдстановки DV у вираз (1) одержуємо
А = р DV = р V1 ( T2 - T1 ) / T1.
Знаходимо розмiрнiсть за останньою формулою:
[A] = Па×м3×К/К = Па×м3 = Н×м = Дж,
i числове значення -
А=1,013×106×2×10-2× 474 - 323)/323 = 9400 Дж.
Задача 6. Яка кiлькicть теплоти поглинається при iзотермiчному розширеннi 0,5 л повітря, якщо тиск зменшується від 58,86×104 до 9,81×104 Па?
Розв'язок
| V = 5×10-4 м3 р1 = 58,86×104 Па р2 = 9,81×104 Па Т = const | В iзотермічному процесі все підведене тепло витрачається на виконання роботи Q =  R T ln R T ln 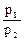 , (1) де m - маса газу; µ - молярна маса; Т - температура газу. , (1) де m - маса газу; µ - молярна маса; Т - температура газу. |
| Q - ? |
Оскільки в цьому процесі об'єм газу зростає (тиск падає), то робота додатня, i для пiдтримання сталої температури тепло Q має пiдводитися.
За законом Менделєєва-Клапейрона визначимо невідому величину температури:
 R T = р1 V1.
R T = р1 V1. 
Тоді Q = р1 V1 ln 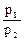 . (2)
. (2)
Використовуючи формулу (2), знаходимо розмірність -
[Q] = Па м3 = Дж,
Числове значення - Q = 523 Дж.
Задача 7. До якого тиску має бути стиснута сумiш повiтря з парою бензину в цилiндрi двигуна, щоб сумiш спалахнула, якщо початковi тиск 1,013.105 Па i температура 273 К, а температура спалаху 833 К. Стиснення вважати адiабатним, газ - двохатомним.
Розв'язок
| i = 5 p = 1,013.105 Па Т = 273 К Т = 833 К | Скористаємось рiвнянням адiабати у виглядi  , (1) де g - показник адiабати, який дорiвнює , (1) де g - показник адiабати, який дорiвнює |
| p - ? |
вiдношенню теплоємностей газу при сталому тиску i при сталому об'ємi:
g = 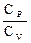 =
= 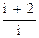 , (2)
, (2)
i - число ступенiв вiльностi молекули газу. Логарифмування формули (1) i пiдстановка значення g призводять до
ln (p) = ln (p0) + 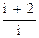
 . (3)
. (3)
Пiдстановка числових значень в формулу (3) i наступне потенцiювання призводять до p = 4,50.106 (Па).
Задача 8. Теплова машина працює за циклом Карно. Температура нагрiвача 500 К. Визначити температуру холодильника i термiчний ККД циклу, якщо за рахунок кожного кiлоджоуля тепла, одержаного вiд нагрiвача, виконується робота 350 Дж.
Розв'язок
| Т1 = 500 К A = 350 Дж Q = 1 кДж | Термiчний ККД визначає частку одержаної теплоти, яка йде на виконання роботи: h = A / Q, (1) де Q - теплота, одержана вiд нагрiвача. |
| Т2, h - ? |
З другого боку, ККД циклу Карно виражається через температуру нагрiвача Т1 i температуру холодильника Т2:
h = 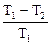 . (2)
. (2)
Порiвнюючи формулу (2) з формулою (1), одержуємо
Т2 = Т1 ( 1- A / Q ) .
Згiдно з рівнянням (1), термiчний ККД виявляється рiвним 0,35 i, згiдно з останнім спiввiдношенням, одержуємо Т2 = 325 К.
Електрика i магнетизм
Задача 1. У скiльки разiв сила електричного вiдштовхування мiж двома протонами бiльша за силу гравiтацiйного притягання мiж ними?
Розв'язок
| m = 1,672×10-27 кг е = 1,6×10-19 Кл G = 6,67×10-11 м 3 / (кг×с2) e0 = 8,85×10-12 Ф / м | Сила вiдштовхування мiж двома протонами у вакуумi може бути знайдена за законом Кулона: Fe = 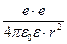 , (1) , (1) |
| Fe / Fg - ? |
де е - заряд протона і r - вiдстань мiж протонами.
Сила притягання мiж протонами визначається за законом всесвiтнього тяжiння:
Fg = 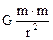 , (2)
, (2)
де m - маса протона; G - гравiтацiйна стала. Подiливши вираз (1) на формулу (2), одержуємо розрахункову формулу
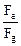 =
= 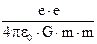 .
.
Розмiрнiсть одержаного результату -
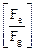 =
= 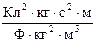 =
=  = [1].
= [1].
Числове значення результату -
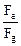 =
= 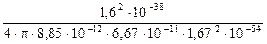 = 1,25×10-36 .
= 1,25×10-36 .
Задача 2. Знайти напруженiсть електричного поля в точцi, яка лежить посерединi мiж точковими зарядами 8×10-9 Кл i - 6×10–9 Кл. Вiдстань мiж зарядами 20 см.
Розв'язок
| q1 = 8×10-9 Кл q2 = - 6×10-9 Кл d = 0,2 м e = 1 e0 = 8,85×10-12 Ф/м | Оскільки заряди мають протилежнi знаки, то напруженостi їх полiв в точцi, яка лежить мiж зарядами, спрямованi в бiк негативного заряду. Результуюча напруженiсть поля за модулем буде дорiвнювати сумi модулiв напруженостей цих полiв. |
| Е - ? |
Модулi напруженості Е1 i Е2 визначаються за формулами
E1 =  , E2 =
, E2 =  ,
,
де r1 = r2 = d/2 - вiдстань вiд заряду до розглядуваної точки.
Сумарна напруженість поля в точцi:
Е = E1 + E2 = 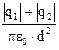 .
.
Розмiрнiсть - [Е] =  =
= 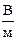 .
.
Числове значення - Е =  = 5,04×104
= 5,04×104 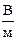 .
.
Задача 3. Безмежна вертикальна площина у вакуумi заряджена рiвномiрно з поверхневою густиною зарядiв 5×10-4 Кл/м2. До нитки причеплена заряджена кулька масою 1 г. Заряди площини i кульки однойменнi. Визначити заряд кульки, якщо нитка утворює з площиною кут 300.
Розв'язок
| m = 10-3 кг s = 5×10-4 Кл / м2 a = 300 e0 = 8,85×10-12 Ф/м g = 9,81 м/с2 | На почеплену кульку дiє вага i сила електричного вiдштовхування Fе. Результуюча сила F зрiвноважується силою натягу нитки N. Як видно з рисунка Fе = m×g×tg×a. (1) Цю ж силу представимо через напруженiсть електричного поля i заряд кульки q: |
| q - ? |
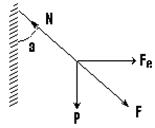
Fе = q×Е . (2)
Напруженiсть поля площини
Е = 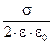 , (3)
, (3)
де s - поверхнева густина зарядiв. Пiдставляючи вираз (3) в формулу (2), а потiм в рівняння (1), одержимо:
m×g×tg a = 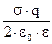 ; q =
; q = 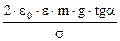 .
.
Розмiрнiсть q за останньою розрахунковою формулою:
[q] = 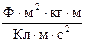 =
= 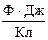 = Ф×В = Кл.
= Ф×В = Кл.
Числове значення -
q = 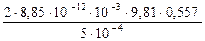 = 1,093×10-9 Кл.
= 1,093×10-9 Кл.
Задача 4. Заряджена порошинка масою 10-10 г зважена в однорiдному електричному полi мiж двома рiзнойменно зарядженими пластинами, вiдстань мiж якими дорiвнює 0,5см. При освiтленнi ультрафiолетовими променями порошинка втрачає заряд i виходить з рiвноваги. Який заряд втратила порошинка, якщо спочатку до пластин була прикладена рiзниця потенцiалiв 154 В, а потiм, щоб повернути в рiвновагу порошинку, додали ще 8 В?
Розв'язок
| m = 10-13 кг d = 5×10-3 м U1 =154 В U = 8 В g = 9,81 м / с2 | До опромiнення порошинка була в рiвновазi, тобто вага iї Р зрiвноважувалась електричною силою F. Вихiдне рiвняння: Р = F. Виражаючи вагу порошинки через iї масу m, а силу F - через напруженiсть електричного поля, |
| Dq - ? |
одержимо
m×g = q×E. (1)
Виражаючи модуль напруженостi поля через рiзницю потенцiалiв Е1 = U1 / d , з рiвняння (1) одержуємо
q1 = (m×g×d ) / U1 . (2)
Так само можна визначити, що пiсля опромiнення порошинки заряд її дорівнюватиме
q2 = ( m×g×d ) / U2 . (3)
За умовою задачi U2 = U1 + DU , тому втрачений порошинкою заряд
Dq = q1 - q2 = m×g×d× (1 / U1 - 1 / U2)
або
Dq =  =
= 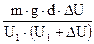 .
.
Розмiрнiсть - [Dq] = 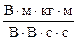 =
=  = Кл.
= Кл.
Числове значення - Dq = 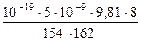 = 1,57×10-18 Кл.
= 1,57×10-18 Кл.
Задача 5. Вилiтаюча при радiоактивному розпадi ядра атому радiю a-частинка зi швидкiстю 1,6×107 м/с зустрiчає ядро натрiю. На яку найменшу вiдстань вона наблизиться до ядра натрiю?
Розв'язок
| v = 1,6×107 м / с m = 4×1,67×10-27 кг q1= 11×e =1,76×10-18 К q2 = 2×e =3,2×10-19 Кл e0 = 8,85×10-12 Ф / м | Найменша вiдстань, на яку може пiдiйти частинка до ядра натрiю, визначається за умовою Wk = Wp , (1) коли кiнетична енергiя Wk - частинки Wk = 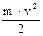 , , |
| r - ? |
перетвориться в потенцiальну енергiю iї вiдштовхування вiд позитивно зарядженого ядра Na:
Wp = 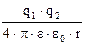 ,
,
де q1 i q2 - заряди частинки i ядра Na; r - вiдстань, на якiй зупиниться частинка бiля ядра Na. Пiдставимо значення енергiй в рівняння (1) i розв’яжемо рiвняння вiдносно r :
r = 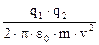 .
.
Розмiрнiсть -
[ r ] =  =
=  =
=  = м.
= м.
Числове значення -
r = 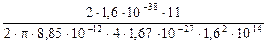 = 6×10-15 м.
= 6×10-15 м.
Задача 6. В серединi плоского конденсатору з площею пластин 200 см2 i вiдстанню мiж ними в 1мм, який заряджено до напруги 300 В, знаходиться скляна пластинка, цiлком заповнюючи простiр мiж пластинами конденсатора. Знайти змiну енергiї конденсатора пiсля вилучення склянної пластинки за таких умов: а) на електродах пiдтримується стала напруга за допомогою джерела струму б) до вилучення скляної пластинки конденсатор вiдiмкнено вiд джерела напруги.
Розв'язок
| S = 2×10-2 м2 d = 10-3 м U = 300 В e = 7 e = 1 e0 = 8,85×10-12 Ф / м | а) Енергiя зарядженого конденсатора зi скляною пластинкою: W1 =  , або пiсля пiдстановки С1 = , або пiсля пiдстановки С1 = 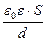 ; W1 = ; W1 =  . . |
| DW - ? |
Якщо на обкладках пiдтримується стала напруга, то пiсля вилучення скла енергiя буде дорiвнювати
W2 = 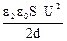 .
.
Змiна енергiї у випадку "а":
DW = W1 -W2 =  .
.
Розмiрнiсть - [DW] = 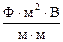 = Ф×В2 = Кл×В = Дж.
= Ф×В2 = Кл×В = Дж.
Числове значення -
DW = 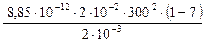 = - 4,78×10-5 Дж.
= - 4,78×10-5 Дж.
б) Якщо конденсатор вiдiмкнуто вiд джерела струму до вилучення склянної пластини, то рiзниця потенцiалiв мiж обкладками пiсля вилучення дiелектрика змiниться, проте збережеться заряд на обкладках (оскільки йому нiкуди подiтися). Енергiю конденсатора в цьому випадку доцiльно подать спiввiдношенням
W1 = 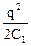 ; W2 =
; W2 =  .
.
Тоді DW = W1 -W2 = 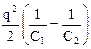 ,
,
або, оскільки q = C1 U, то
DW = 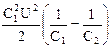 =
= 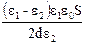 .
.
Числове значення -
DW =  = 3,35×10-4 Дж.
= 3,35×10-4 Дж.
У випадку "а" енергiя конденсатора зменшилась, а у випадку "б" - збiльшилась.
Задача 7. Визначити ККД акумулятора, ЕРС у якого дорiвнює 2,15 В, якщо вiн подає у зовнiшнє коло струм силою 5 A. Внутрiшнiй опiр акумулятора 0,18 Ом.
Розв'язок
| Е = 2,15 В I = 5 A r = 0,18 Ом | ККД джерела струму дорiвнює вiдношенню енергii, що витрачає джерело струму у зовнiшньому колi, до всiєї витраченої енергiї: h =  , (1) , (1) |
| h - ? |
Визначимо зовнiшнiй опiр кола за допомогою закону Ома для контура:
I = 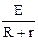 Þ R =
Þ R = 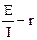 .
.
Пiдставляючи значення R в рівняння (1), одержуємо
h = 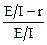 =
= 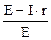 .
.
Числове значення ККД дорiвнює
h = 1- 0,90 / 2,15 = 0,58.
Задача 8. На кiнцях залiзного проводу довжиною 1,5 м i радiусом перерiзу 0,3 мм пiдтримується напруга 1,0 В. Визначити: 1) потужнiсть, яка споживається у проводi; 2) кiлькiсть тепла, яке видiляється у проводi за 1 год; 3) густину струму; 4) число електронiв, що проходить через поперечний перерiз проводу за 1 с.
Розв'язок
| I = 1,5 м U= 1,0 В е = 1,6×10-19 Кл r = 8,7×10-8 Ом×м r = 3×10-4 м t1 = 3600 c t2 = 1 c | 1. Потужнiсть, яка споживається у провiднику, визначається силою струму i напругою: P = I×U. (1) Силу струму знайдемо за законом Ома для дiлянки кола: I = U / R. (2) Опiр провiдника за його геометричними розмірами визначається так: |
| P, Q, j, N - ? |
R = 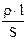 =
= 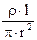 , (3)
, (3)
де r - питомий опiр матерiалу провiдника; l - довжина провiдника; S - площа поперечного перерізу провідника. Пiдставляючи формулу (3) в формулу (2), маємо
I = 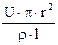 . (4)
. (4)
Числове значення сили струму
I =  = 1,44 A.
= 1,44 A.
Згiдно з формулою (1), потужнiсть дорiвнює
P = I×U = 1,44 A×1,0 В = 1,44 Вт.
2. Кiлькiсть теплоти, що видiляється в провiднику за 1 годину, визначимо за формулою
Q = I×U×t = 1,44 A×1,0 В×3600 c = 5,18×103 Дж.
3. Густину струму визначимо за спiввiдношенням
j = I / S = I / ( p×r2 ) = 1,44 A / ( p×9×10-8 м2 ) = 5,09×106 A / м2 = 5,1 A/мм2.
4. Число електронiв N, що проходять через поперечний перерiз провiдника за 1 с, знайдемо за спiввiдношенням
N = 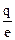 =
=  ,
,
де q - заряд, що пройшов через поперечний перерiз провiдника за час t2; e - заряд електрона.
Числове значення - N = 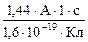 = 9×1018.
= 9×1018.
Задача 9.Вiд джерела, рiзниця потенцiалiв на клемах якого 105 В, треба передати потужнiсть 50 кВт на вiдстань 5 км. Допускаються втрати напруги в проводах 1%. Розрахувати найменший перерiз мiдного проводу, придатного для цiєї мети.
Розв'язок
U = 105 В P = 5×104 Вт n = 0,01  = 5×103 м r = 1,7×10-8 Ом×м = 5×103 м r = 1,7×10-8 Ом×м | Падiння напруги в проводах U = I×R, (1) пропорцiональне опору проводiв: R = 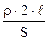 , (2) де r - питомий опiр провода; 2× , (2) де r - питомий опiр провода; 2×  -довжина -довжина |
| S - ? |
проводiв (два проводи!); S - перерiз провода.
Струм I можна знайти за потужнiстю i напругою на клемах джерела струму:
I = 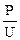 . (3)
. (3)
Враховуючи, що падiння напруги в проводах має становити не бiльше нiж частку n вiд прикладеної напруги
U1 = n×U , (4)
прирiвняємо вирази (1) i (4) i пiдставимо значення I i R iз формул (2) i (3):
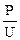
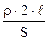 = n×U або S =
= n×U або S = 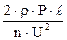 .
.
Розмiрнiсть - [S] =  = м2
= м2
Числове значення -
S = 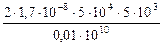 = 8,510-8 м2.
= 8,510-8 м2.
Задача 10. До двох батарей, з'єднаних паралельно, пiдiмкнули електричну лампу. Який опiр має бути у лампи, аби вона споживала максимальну потужнiсть? Визначити максимальну потужнiсть при ЕРС батарей 12 В i 10 В i однакових внутрiшнiх опорах батарей по 1 Ом.
Розв'язок
| Е1 = 12 В Е2 = 10 В r1 = r2 = 1Ом | Для розв'язку задачi застосуємо закони Кiрхгофа для розгалужених кiл. Для цього позначимо на схемi напрямки струмiв i виберемо напрямок обходу контурiв На схемi маємо два вузли - F i C. За першим законом Кiрхгофа можна скласти тiльки одне рiвняння. Сума струмів, що знаходяться, |
| R, P - ? |
 наприклад, у вузлі С:
наприклад, у вузлі С:
I1 + I2 – I = 0 (1)
Застосуємо другий закон Кiрхгофа, запишемо для контура ABDE (обхід за годинниковою стрілкою!) :
I1 × r1+ I× R = Е1 (2)
Для контура FCDE;
I2 × r2+ I× R = Е2 . (3)
Рiвняння (1) - (3) утворюють систему, за допомогою якої можна визначити три елементи електричного кола. Визначаючи I1 та I2 iз виразів (2) та (3) i пiдставляючи їх значення в формулу (1), знаходимо значення струму в лампi, виражене через iї опiр:
I =  . (4)
. (4)
Потужнiсть, що споживається електролампою, подамо так:
P = I2×R = (Е1 + Е2 )2  = 0 . (5)
= 0 . (5)
Для визначення опору R = R0 , за яким лампа споживає максимальну потужність, продиференцiюємо рівняння (5) за R i прирiвняємо похiдну до нуля:
(Е1 + Е2 )2  = 0,
= 0,
звiдки одержуємо R0 = r/2. Оскiльки величина Р позитивна, то це значення R вiдповiдає максимуму, в чому легко впевнитися, застосувавши метод змiни знаку першої похiдної при переходi через значення R. З урахуванням того, що R0 = r/2, за формулою (5) обчислюємо максимальну потужнiсть лампи:
Pмах = (Е1 + Е2 )2  =
=  = 60,5 Вт.
= 60,5 Вт.
Задача 11.По двох довгих прямолiнiйних проводах, якi розмiщенi на вiдстанi 5 см один вiд одного, течуть струми по 10 А. Визначити напруженiсть магнiтного поля, що створюється в точцi, яка лежить посерединi мiж проводами у випадках, коли струми течуть: 1) в одному напрямку; 2) в протилежних напрямках.
Розв'язок
I1 =  I2 = 10 A R = R / 2 = 2,5×10-2 м I2 = 10 A R = R / 2 = 2,5×10-2 м | Результуюча напруженiсть магнiтного поля дорiвнює векторнiй сумi полiв, створюваних струмами I1 i I2. Напрямок полiв струмiв у точцi мiж проводами знаходимо за |
| Н - ? |
 правилом буравчика, абсолютну величину - за формулою
правилом буравчика, абсолютну величину - за формулою
H = 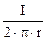 , (1)
, (1)
де r - вiдстань вiд прямолiнiйного довгого провiдника.
В данiй задачi абсолютнi значення напруженостей вiд обох провiдникiв однаковi:
H1 = H2 = 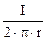 =
=  = 63,6 А/м.
= 63,6 А/м.
У випадку однаково спрямованих струмiв у точцi мiж проводами вектори Н1 i Н2протилежнi. Результуюча напруженiсть дорiвнює за модулем рiзницi модулiв Н1 i Н2:
Н = Н1 - Н2 = 0.
У випадку, коли струми течуть у протилежних напрямках, модуль результуючої напруженостi дорiвнює сумi модулiв:
Н = Н1 + Н2 = 127,3 А/м.
Якщо змiнити напрямок Н2 на протилежний, то Н спрямований вниз.
Задача 12. Знайти кiнетичну енергiю протона, який рухається по дузi кола радiусом 60 см в магнiтному полi, iндукцiя якого дорiвнює 1 Тл i перпендикулярна до напрямку швидкостi протона.
Розв'язок
| r = 0,6 м B = 1 Тл е = 1,6×10-19 Кл a = 900 m = 1,672×10-27 кг | Кiнетична енергiя визначається за формулою Wk = 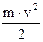 . (1) При русi в магнiтному полi на заряджену частку з боку магнiтного поля перпендикулярно до швидкостi дiє сила Лоренца, яка вiдiграє роль . (1) При русi в магнiтному полi на заряджену частку з боку магнiтного поля перпендикулярно до швидкостi дiє сила Лоренца, яка вiдiграє роль |
| Wk - ? |
доцентрової сили: 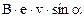 =
= 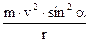 . (2)
. (2)
Iз рівняння (2) визначаємо швидкiсть частинки:
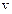 =
= 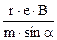 .
.
Пiдставивши v в формулу (1), одержимо
Wk = 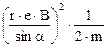 .
.
Розмiрнiсть -
[ Wk ] =  =
=  =
=  = Дж.
= Дж.
Числове значення -
Wk = 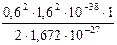 = 27,68×10-13 Дж.
= 27,68×10-13 Дж.
Задача 13. Дротяна рамка розмiщена перпендикулярно до магнiтного поля, iндукцiя якого змiнюється за законом В = В0 × [ 1-exp(-k×t) ], де В0 = 0,5 Тл; k = 0,1 с-1 . Визначити величину ЕРС, яка iндукується в контурi в момент t = 2,3 с. Площа рамки S = 0,04 м2.
Розв'язок
| В0 = 0,5 Тл k = 0,1 с -1 S = 0,04 м2 t = 2,3 с | Величина ЕРС, що iндукується в контурi, визначається за законом Фарадея: Е = -  , (1) де Ф – магнітний потік через контур. , (1) де Ф – магнітний потік через контур. |
| Е - ? |
В даному випадку
Ф =В×S = В0 ×S × [1-exp(-k×t) ] . (2)
Підставляючи формулу (2) в формулу (1) , одержуємо
Е = - k×В0×S×exp(-k×t).
Розмірність Е не залежить від показника експоненти, оскільки він безрозмірний. Розрахуємо розмірність Е:
[Е] = 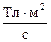 =
= 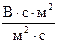 = B.
= B.
Числове значення -
Е = 0,5 ×0,04 × exp(-0,1×2,3 ) = 2,06×10-3 B.
Задача 14. У коливальному контурі з індуктивністю 0,01 Гн відбуваються затухаючі коливання, причому заряд конденсатора зменшується у 10 разів за час одного періоду 10-5 с. Визначити опір контура.
Розв'язок
| L = 0,01 Гн q0/q = 10 T = 10-5 с | При затухаючих коливаннях заряд на обкладках конденсатора змінюється за законом q = q0 × e -R×t/2×L × cos (w×t). (1) При t = 0 заряд на конденсаторі дорівнює q0, а через період - |
| R - ? |
q = q0 × e -R×T/2×L × cos (2×p) = q0 × e -R×T/2×L . (2)
Звідси одержуємо R =  ×
× 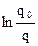 .
.
Розмірність - [R] =  =
= 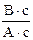 = Ом.
= Ом.
Числове значення - R =  = 4605 Ом.
= 4605 Ом.
Задача 15. Одношарова обмотка котушки довжиною 50 см і діаметром 5 см складається з 500 витків проводу перерізом 1 мм2. При якій частоті змінного струму її імпеданс вдвічі більший від опору ?
Розв'язок
| l = 0,5 м S1 = 10-6 м2 N = 500 d = 0,05 м r = 1,7 10-8 Ом×м m0 = 4×p×10-7 Гн/м | За умовою задачі імпеданс вдвічі більший опору: Z = 2R. (1) Імпеданс котушки - Z = 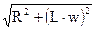 . (2) З рівнянь (2) і (1) одержуємо значення w . (2) З рівнянь (2) і (1) одержуємо значення w |
| n - ? |
циклічної частоти: w = 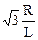 .
.
Визначимо R і L через параметри котушки:
R =  , L =
, L = 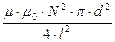 ,
,
де ( N×p×d ) - довжина провода. Підставляючи R і L у вираз для w, одержуємо n = 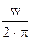 =
= 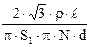 .
.
Розмірність - [n] = 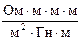 =
= 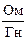 =
= 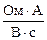 =
=  = Гц.
= Гц.
Числове значення - n = 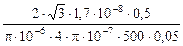 = 300 Гц.
= 300 Гц.
Оптика, фізика атома, ядра, твердого тіла
Задача 1. Від двох когерентних джерел (l = 0,8 мкм) промені попадають на екран, на якому спостерігають інтерференційну картину. Коли на шляху одного з променів, перпендикулярно йому, розташували мильну плівку ( n = 1,33 ), інтерференційна картина змінилася на протилежну. При якій найменшій товщині плівки це можливо?
Розв'язок
| l = 0,8 мкм n = 1,33 | Зміна інтерференційної картини на протилежну означає, що на тих місцях екрану, де спостерігалися максимуми освітленості, почали спостерігати мінімуми і навпаки. Таке можливо при зміні оптичної |
| d мін - ? |
різниці ходу променів на непарне число напівдовжин хвилі.
У разі мінімальної товщини плівки це 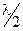 .
.
Якщо товщина плівки dмін , то
d мін ×( n – 1 ) = 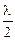 ,
,
звідки d мін =  =
=  = 1,21 мкм.
= 1,21 мкм.
Задача 2. Визначити концентрацію цукрового розчину, якщо при проходженні світла через трубку з цим розчином довжиною 20 см площина поляризації світла повертається на кут 10°. Питоме повертання цукру у розчині 0,6 град/(дм×%).
Розв'язок
