Характеризующие термодинамические свойства

Влажного воздуха

Влажный воздух, образующий атмосферу Земли, является смесью сухого воздуха и водяного пара. Сухой воздух − смесь 11 газов, основными из которых являются азот (75,5 % общей массы воздуха), кислород (23,15 %), аргон (1,286 %) и диоксид углерода (0,04 %). Давление атмосферного воздуха на уровне океана равно примерно 0,1 МПа. Температура атмосферного воздуха изменяется в интервале от –50 °С до +50 °С. При таких параметрах сухой воздух подчиняется законам идеального газа, и для него справедливы уравнение Клапейрона

pс.в·vс.в=Rс.в·T

(5.1)

и закон Дальтона

,

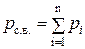(5.2)

где p_i − парциальные давления компонентов сухого воздуха;

v_с.в.– объём 1 кг сухого воздуха;

R_с.в. = 287,1 кДж/(кг·К) – удельная газовая постоянная водяного пара.

Водяной пар, находящийся во влажном воздухе, также хорошо подчиняется законам идеального газа. Так уравнение состояния для d_пкг водяного пара, приходящегося на 1 кг сухого воздуха, имеет вид

рп·vс.в = dп RпT,

(5.3)

где р_п − парциальное давление водяного пара, Па;

v_с.в − удельный объем сухого воздуха, м³/кг с.в.;

d_п − количество пара, кг, содержащееся в 1 кг сухого воздуха (эту величину называют паросодержанием влажного воздуха);

R_п = 461,0 кДж/(кг·К) – удельная газовая постоянная водяного пара.

Поскольку влажный воздух является смесью сухого воздуха и водяного пара и оба компонента подчиняются законам идеального газа, влажный воздух можно рассматривать как идеальный газ.

Сложив уравнения (5.1) и (5.3), получим уравнение состояния влажного воздуха, отнесенное к 1 кг сухого воздуха

рб·vс.в=Rвл.в ·T

(5.4)

где р_б=р_с.в.+р_п − барометрическое (полное давление) влажного воздуха, Па;

R_вл.в=R_с.в+dR_п = 287,1+461,0d − удельная газовая постоянная влажного воздуха, имеющая размерность Дж/(кг с.в.·К).

В технике кондиционирования учитывается температурная зависимость энтальпии сухого воздуха: при температуре 0°С принимается равной нулю, а при других температурах рассчитывается из соотношения

hcв = cp с.в·t

(5.5)

Значение теплоемкости с_р,с.в. принимается равным 1,00485 кДж/(кг с.в.·К).

Начало отсчета энтальпии водяного пара принято от состояния насыщенной жидкости при температуре 0 °С. Поэтому энтальпия перегретого водяного пара рассчитывается из соотношения

hп = ros+cp, п·t = 2501+cp,п·t

(5.6)

где r_os = 2501 кДж/кг – теплота парообразования водяного пара при темпера-туре 0 °С;

с_р,п – изобарная теплоемкость пара, принимаемая равной 1,93 кДж/(кг·К).

Энтальпия влажного воздуха, как аддитивная величина энтальпии сухого воздуха и водяного пара, рассчитывается из соотношения, полученного сложением уравнений (5.5) и (5.6), причем последнее умножается на d

Нвл.в=hс.в.+d·hп=cр, с.в ·t+d(2501+1,93·t)=c'р,вл.в ·t+2501·d

(5.7)

Здесь с'_р,вл.в. = с_р,с.в.+d·с_р,п – теплоемкость влажного воздуха, отнесенная к одному кг сухого воздуха.

В зависимости от соотношения температуры, влагосодержания и общего (барометрического) давления влажный воздух может находиться в трех состояниях: ненасыщенном, насыщенном и пересыщенном.

Приведенные выше уравнения (5.1)-(5.7) справедливы лишь для гомогенных смесей, то есть для ненасыщенного и насыщенного влажного воздуха.

Для характеристики состояния влажного воздуха используются также понятия влагосодержание, относительная влажность, абсолютная влажность и плотность влажного воздуха.

Различают массовое и мольное влагосодержание.

Массовым влагосодержанием (d) называется отношение массы влаги, содержащейся во влажном воздухе (М_воды) к массе сухого воздуха (М_возд), то есть количество влаги, приходящейся на 1 кг сухого воздуха

.

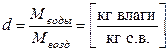(5.8)

Мольное влагосодержание х − отношение числа молей влаги к соответствующему числу молей сухого воздуха

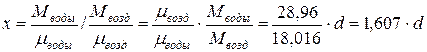(5.9)

или

d = 0,622·x .

(5.10)

Величины d и x, рассчитываемые из соотношений (5.8)-(5.10), характеризуют влажный воздух, в котором влага может находиться как в виде пара, так и в виде капель жидкости или кристаллов льда.

Если влага в воздухе находится только в виде пара, то

.

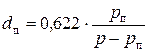(5.11)

Величина d_п называется паросодержанием.

В случае, когда влажный воздух находится при атмосферном давлении В,

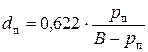(5.12)

Максимально возможное паросодержание d_s насыщенного влажного воздуха при заданной температуре рассчитывается из соотношения

.

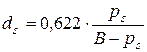(5.13)

Относительной влажностью называется отношение парциального давления водяного пара, содержащегося во влажном воздухе, к давлению насыщения водяного пара при данной температуре. Относительную влажность можно рассматривать также как отношение фактической плотности пара в смеси к плотности насыщенного пара при той же температуре

.

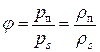(5.14)

Значения φ выражаются в процентах (от 0 до 100 %) либо в долях единицы (от 0 до 1). Уравнение (5.12) для расчета паросодержания ненасыщенного влажного воздуха может быть преобразовано с учетом соотношения (5.14) к виду

.

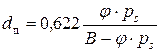(5.15)

Абсолютной влажностью называется масса водяного пара, содержащегося в одном м³ влажного воздуха.

Плотность влажного воздуха (кг/м³) рассчитывается из уравнения

,

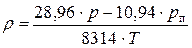(5.16)

где р_п – парциальное давление водяных паров, Па;

р – полное (атмосферное) давление влажного воздуха, Па.

Используя уравнения (5.7) и (5.15), можно рассчитывать и исследовать процессы тепловлагообмена во влажном воздухе. Однако для инженерных расчетов и анализа процессов тепломассообмена во влажном воздухе широкое применение нашла косоугольная тепловая H,d диаграмма влажного воздуха (рис. 5.1). Поскольку в уравнение (5.15) входят три независимых переменных, то при построении тепловой диаграммы необходимо зафиксировать один параметр. Обычно фиксируют барометрическое давление В, так как в земных условиях оно изменяется незначительно.

На диаграмме по оси абсцисс откладывается влагосодержание влажного воздуха d (г влаги)/(кг сухого воздуха), а по оси ординат — энтальпия H. При фиксированном полном давлении влажного воздухам, его термодинамическое состояние определяется двумя независимыми переменными (пересечение изолиний которых на диаграмме и определяет точку А). Если положение точки А известно (см.рис.5.1), то могут быть определены следующие параметры влажного воздуха в этой точке: t_А– температура по сухому термометру (истинная температура влажного воздуха); t_τА– температура по мокрому термометру (температура насыщения влажного воздуха); t_рА – температура точки росы (температура, при которой в процессе чистого охлаждения влажного воздуха из него начинает выпадать влага в виде жидкости либо твердой фазы); d_А – влагосодержание; φ_А – относительная влажность; H_А – энтальпия; р_пА – парциальное давление пара во влажном воздухе. Параметры d_А , t_рА и р_пА являются взаимозависимыми, то есть каждый из них однозначно определяет два остальных. Поэтому любая комбинация из них не определяет термодинамическое состояние влажного воздуха. Энтальпия H_А является функцией состояния, рассчитываемой из уравнения (5.7), а парциальное давление пара р_пА хотя и есть независимой переменной, не может быть определено экспериментально.

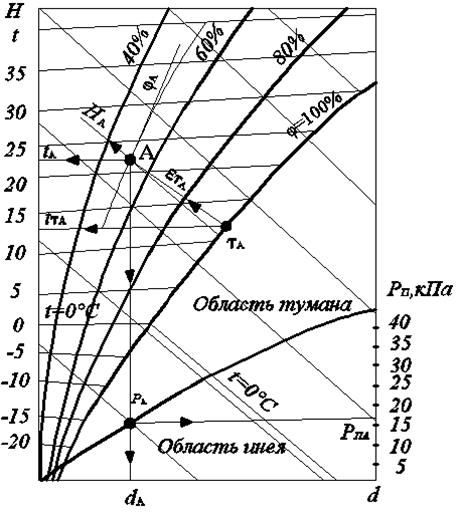
Рис. 5.1. Косоугольная тепловая диаграмма H,d влажного воздуха

На диаграмме нанесены изолинии основных параметров влажного воздуха:

– прямые линии постоянных температур (изотермы t= idem), расходящиеся веером относительно изотермы 0°С (изотермы, соответствующие положительным температурам – восходящие прямые, а отрицательным – ниспадающие);

– прямые линии постоянной энтальпии (изоэнтальпы H =idem) – прямые, наклонённые под углом примерно 45 ° к координатным осям H,d (с тем условием, чтобы изотерма 0°С была горизонтальной);

– вертикальные прямые линии постоянного влагосодержания (d =idem);

– кривые линии постоянной относительной влажности (изофиты φ = idem), включая линию состояния насыщенного влажного воздуха φ = 100 %;

– линия парциальных давлений водяного пара, p_п = f(t,d).

Положение линии φ = 100 % зависит от полного давления влажного воздуха: чем оно больше, тем левее и круче располагается эта линия.

Все процессы тепломассообмена во влажном воздухе изображаются на диаграмме H,d непрерывными линиями.

Направление процесса тепломассообмена характеризуется уклоном процесса ε и/или коэффициентом влаговыпадения ξ. Уклон процесса рассчитывается из соотношения

.

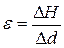(5.17)

Следовательно, ε является отношением полного изменения энтальпии влажного воздуха в процессе тепловлагообмена ΔH (полной теплоты) к соответствующему изменению влагосодержания Δd. Величина εизменяется от +∞ до -∞.

Коэффициент влаговыпадения ξрассчитывается из соотношения

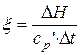(5.18)

и является отношением полной теплоты в рассматриваемом процессе ΔH к ощутимой теплоте c_р'·Δt, идущей на изменение температуры воздуха.

Расчеты процессов тепломассообмена во влажном воздухе могут выполняться как аналитически (с помощью приведенных выше уравнений), так и графически (с помощью H,d диаграммы). Аналитические методы расчета более точны, но громоздки; графические – менее точны, но более просты и наглядны.

Изобарная теплоемкость влажного воздуха c_р' в соотношении (5.18) при графическом методе решения задач принимается равной единице. При аналитическом решении необходимо учитывать зависимость теплоемкости от влажности и рассчитывать c_р' из соотношения

с'р = ср,с.в.+ср,п·dп ,

(5.19)

где c_р.с.ви c_р,п – удельные массовые изобарные теплоемкости сухого воздуха и водяного пара при соответствующей температуре, кДж/(кг·К);

d_п – паросодержание воздуха, (кг пара/кг с.в.).

Температурную зависимость теплоемкостей c_р.с.ви c_р,п можно не учитывать, так как температура воздуха в процессах тепломассообмена изменяется в сравнительно узких пределах.

При тепловлажностной обработке воздуха наблюдается недорекуперация в соответствующих процессах, то есть влажный воздух недоохлаждается (недонагревается) и/или недоосушается (недоувлажняется) по сравнению с температурой и влагосодержанием среды либо поверхности, с которой он взаимодействует. Это явление характеризуется коэффициентами охлаждения (нагрева) η_t, и осушения (увлажнения) η_d воздуха, рассчитываемыми из уравнений

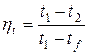	(5.20)
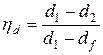	(5.21)

где t₁, t₂ и d₁, d₂ – температура и влагосодержание воздуха на входе и выходе из аппарата при его обработке соответственно;

t_f, d_f – температура и влагосодержание воздуха, равновесного с параметрами поверхности аппарата или среды, с которой воздух взаимодействует.

Часто встречается процесс смешения двух или нескольких потоков воздуха, отличающихся по массе и состоянию. Такой процесс можно рассчитать с помощью диаграммы H,d. Пусть точка 1 характеризует воздух массой М₁ с энтальпией Н₁, а точка 3 – воздух массой М₃ с энтальпией Н₃ (рис.5.2). Тогда состояние воздуха после смешения этих потоков (точка 4) может быть определено из уравнений баланса теплоты и влаги

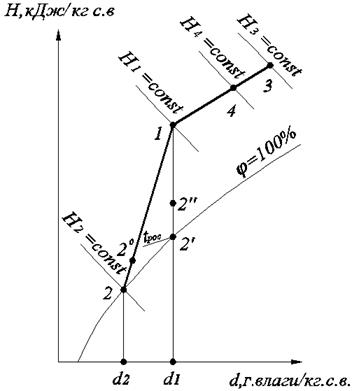
Рис.5.2. Процессы охлаждения, осушения и смешения воздуха

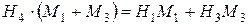	(5.22)
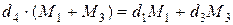.	(5.23)

Решая совместно уравнения (5.22) и (5.23), находим

.

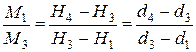(5.24)

Это тождество определяет уравнение прямой линии, проходящей через три точки с координатами (Н₁, d₁; Н₄, d₄и Н₃, d₃). Таким образом, точка 4, характеризующая состояние смеси двух потоков, принадлежит прямой, соединяющей точки 1и 3. Точка 4 делит отрезок прямой 1-3 на части, обратно пропорциональные массам смешиваемых потоков воздуха.

Особое место среди процессов, осуществляемых во влажном воздухе, занимают процессы, занимающие промежуточное положение между процессами чистого охлаждения и чистого осушения, Такие процессы характеризуют охлаждение и осушение воздуха в воздухоохладителях (рис.5.2, процесс 1-2). Если температура поверхности воздухоохладителя выше точки росы воздуха t_рос. окончания изменения состояния воздуха будет характеризоваться точкой 2'', лежащей на прямой 1–2' выше точки 2'. В случае равенства температур поверхности воздухоохладителя и точки росы воздуха, теоретически предельное конечное состояние воздуха будет характеризоваться точкой 2', лежащей на линии насыщения. Если же температура поверхности охладителя ниже t_рос., воздух будет одновременно охлаждаться и осушаться, направление этого процесса условно изображается прямой 1–2, а конечное состояние воздуха – точкой 2⁰, лежащей на прямой 1-2, выше точки 2. В результате процесса 1-2влагосодержание воздуха снизится на Δd = d₁-d₂⁰. Отводимая при этом теплота определяется разностью энтальпий H₁-H₂⁰.