Энергитические зоны в кристаллах.теорема Блоха.Зонная структура энергет-го спектра электронов

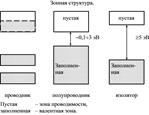
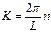расположение энергетических зон, разрешенных и запрещенных.На рис. энергетический спектр электронов кристалле имеет зонную структуру.L – длина кольца цепочки.Значения волновых векторов . Зону, произошедшую от валентных уровней атомов, образующих кристалл, называют валентной зоной.Зоны, произошедшие от внутренних уровней, всегда полностью заполнены электронами Частично заполненной или незаполненной может быть внешний валентный уровень (зона проводимости).Наиболее слабо связаны 3S-электроныПространственная протяженность электронных волновых функций зависит от квантовых чисел. Для больших квантовых чисел электронные волновые функции простираются на большие расстояния от ядра, для этих уровней взаимное влияние атомов будет проявляться при больших расстояниях между атомами.Твердое тело из четырех атомов будет иметь всего четыре уровня, распределенные по некоторому энергетическому интервалу.Эффект сближения атомов проявляется в увеличении общего числа уровней. В реальном теле содержится порядка 10²³ отдельных уровней, которые непрерывно распределяются внутри некоторого интервала, образуя зону разрешенных значений энергии. Такая же ситуация в основном имеет место для валентных электронов любого атома..Полупроводники и изоляторы отличаются друг от друга только шириной запрещенной зоны.Теорема Блоха утверждает, что собственные функции волнового уравнения с периодическим потенциалом имеют вид произведения функции плоской волны 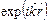.На функцию 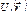, которая является периодической функцией в кристаллической решетке: 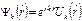Волновую функцию называют функцией Блоха. Решения уравнения Шредингера такого вида состоят из бегущих волн, из таких решений можно составить волновой пакет, который будет представлять электрон, свободно распространяющийся в периодическом потенциальном поле, созданном ионными остовами.Форма волнового пакета при t=0 для дебройлевских волн 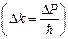. Амплитуда 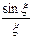указана штриховой линией, волна – сплошной. Движение монохроматической плоской волны вдоль оси Х можно описать функцией 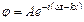.Скорость распространения волны может быть найдена как скорость перемещения постоянной фазы. 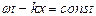.Если время изменится на ∆t,координата должна измениться на ∆х, которая может быть найдена из равенства 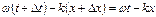т.е. 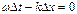Отсюда скорость распространения постоянной фазы, получившей название фазовой скорости: 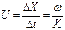Фазовая скорость электрона, движущегося со скоростью V, можно написать 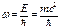, , 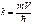, 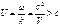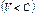для описания электрона в атоме мы должны использовать волновое уравнение, т.к. волновой пакет расплывается практически мгновенно.Волновое уравнение фотона содержит вторую производную по времени, т.к. фотон всегда релятивистская частица. Энергетические зоны являются следствием периодической структуры кристалла и представляют собою фундаментальные характеристики электронной структуры твердого тела. 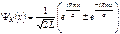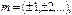Волновая функция имеет вид: 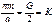Рассмотрим мысленно «процесс образования» твердого тела из изолированных атомов. Пока атомы изолированы, они имеют совпадающие схемы энергетических уровней. По мере «сжатия» нашей модели до кристаллической решетки, взаимодействие между атомами приводит к тому, что энергетические уровни атомов смещааются, расщепляются и расширяются в зоны, образуется зонный энергетический спектр. Образование зонного энергетического спектра в кристалле является квантово-механическим эффектом в вытекает из соотношения неопределенностей.