Общие подходы к решению прямых задач электроразведки
В основе теории электроразведки лежат уравнения Максвелла, являющиеся постулатами макроскопической электродинамики. Они включают в себя все основные законы электромагнетизма (законы Ома, Ампера, Кирхгофа и др.) и описывают поля в разных средах. Из уравнений Максвелла получается дифференциальное уравнение, названное телеграфным. Решая его, можно получить электрическую ( 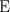 ) компоненту поля в средах вдали от источника с электромагнитными параметрами
) компоненту поля в средах вдали от источника с электромагнитными параметрами 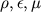 :
:
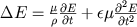 , где , где 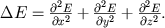 | (3.5) |
Дифференцирование ведется по декартовым координатам ( х, у, z) и времени (  ). Уравнение для магнитной (
). Уравнение для магнитной (  ) компоненты поля аналогично.
) компоненты поля аналогично.
Если геоэлектрический разрез известен, то с помощью уравнения (3.5) и физических условий задачи, называемых условиями сопряжения, решаются прямые задачи электроразведки, т.е. получаются аналитические или численные значения 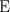 и
и  , которые соответствуют заданному геоэлектрическому разрезу. В теории электроразведки прямые задачи решаются для разных физико-геологических моделей (ФГМ) сред. Под ФГМ понимаются абстрактные геоэлектрические разрезы простой геометрической формы, которыми аппроксимируются реальные геолого-геофизические разрезы. Сложность решения прямых задач заключается в выборе моделей, близких к реальным, но таких, чтобы для избранного типа первичного поля удалось получить хотя бы приближенное решение для
, которые соответствуют заданному геоэлектрическому разрезу. В теории электроразведки прямые задачи решаются для разных физико-геологических моделей (ФГМ) сред. Под ФГМ понимаются абстрактные геоэлектрические разрезы простой геометрической формы, которыми аппроксимируются реальные геолого-геофизические разрезы. Сложность решения прямых задач заключается в выборе моделей, близких к реальным, но таких, чтобы для избранного типа первичного поля удалось получить хотя бы приближенное решение для 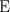 или
или  . Для этого применяется математическое моделирование с использованием современных ЭВМ. В недалеком прошлом основным способом решения прямых задач для сложных ФГМ и разных по структуре типов полей являлось физическое моделирование на объемных или плоскостных моделях сред.
. Для этого применяется математическое моделирование с использованием современных ЭВМ. В недалеком прошлом основным способом решения прямых задач для сложных ФГМ и разных по структуре типов полей являлось физическое моделирование на объемных или плоскостных моделях сред.
Наиболее простыми моделями сред являются:
однородное изотропное пространство или полупространство с одинаковыми электромагнитными свойствами (решения над ними называются соответственно первичным или нормальным полем источника);
анизотропное пространство или полупространство с электромагнитными свойствами, отличающимися в направлении и вкрест слоистости пород;
одномерные неоднородные среды, в которых свойства меняются в одном направлении. Такими ФГМ могут быть, например, вертикальные контакты двух сред, ряд вертикальных пластов или горизонтально слоистая среда с разными  ;
;
двухмерные неоднородные среды, в которых электромагнитные свойства меняются в двух направлениях. Примером могут быть наклонные пласты или цилиндры, простирающиеся вдоль одного направления и отличающиеся по  от вмещающих горных пород;
от вмещающих горных пород;
трехмерные неоднородные среды, в которых свойства меняются по трем направлениям. Самой простой из подобных моделей является шар с разными 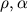 или
или  в однородном полупространстве.
в однородном полупространстве.
В порядке увеличения сложности структуры первичных полей, а значит возрастания сложности решения прямых задач, используемые для электроразведки поля можно расположить в следующей последовательности: точечных и дипольных источников постоянного тока, плоских гармонических электромагнитных волн, сферических волн дипольных гармонических или импульсных источников, цилиндрических волн длинного кабеля и т.п.
Существуют различные подходы к решению прямых задач с помощью уравнения (3.5). Любое правильное решение, удовлетворяющее всем физическим требованиям, единственно и корректно. Под корректностью понимается такое решение, в котором малым изменениям исходных данных соответствуют малые приращения расчетных параметров.
