Обработка результатов измерений. 1. Определить перепад давлений на концах капилляра:

1. Определить перепад давлений на концах капилляра:

Δр = ρ_воды gΔh

2. Определить расход воздуха в установке, используя соотношение Пуазейля:

,

где G = V/t, V – объём воздуха, пошедшего через нагреватель за время t.

3. Рассчитать массовый расход воздуха по формуле m/t = G r_{воздуха,} Он
остается постоянным в течение всего опыта, т.к. Dh=const.

4. На основании формул (4) и (5) рассчитать значения I_Н и Q/t соответственно, данные занести в таблицу.

5. Используя градуировочную зависимость для термопары “хромель-копель” (см. справочник), определить разность температур DТ для каждого значения e. Полученные данные занести в таблицу.

6. Искомое значение с_Р найти по формуле (6).

7. Определить погрешность измерения величины с_Р

8. Построить график зависимости с_Р от температуры воздуха в нагревателе Т = Т_л + ΔТ и сравнить с табличными значениями.

Контрольные вопросы

1. Что называют числом степеней свободы (молекулы)?

2. Сколько и какие степени свободы имеет двух, трех, четырехатомные молекулы?

3. Какой газ называют идеальным?

4. Что такое внутренняя энергия идеального газа и как она зависит от числа степеней свободы молекул, составляющих газ?

5. В чем заключается различие понятий внутренней энергии, теплоты и работы?

6. Сформулировать и записать первое начало термодинамики.

7. Дать определение изохорному и изобарному процессам (графическое изображение и их характеристики).

8. Что такое теплоемкость? Как она зависит от способа нагревания газа?

9. Вывести формулы для определения молярной теплоемкости при изохорном и изобарном процессах.

10. Дать определение молярной теплоемкости, удельной теплоемкости, показать связь между ними.

11. Объяснить методику измерения теплоемкости воздуха при постоянном давлении методом протока.

12. Первый закон термодинамики утверждает невозможность построения вечного двигателя. Почему?

Лабораторная работа № 3

ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ ПРИ ФАЗОВОМ ПЕРЕХОДЕ

Цель работы: определение изменения энтропии при фазовом переходе на примере кристаллизации олова из расплава при его охлаждении. Определение температуры и удельной теплоты кристаллизации олова.

Введение

В термодинамике фаза определяется как равновесное состояние вещества, которое по своим физическим свойствам существенно отличается от других возможных равновесных состояний этого вещества. Переход вещества из одной фазы в другую называется фазовым переходом или фазовым превращением. К фазовым переходам первого рода относятся превращения, характеризуемые следующими основными свойствами:

а) поглощение или выделение скрытой теплоты перехода;

б) различие плотностей фаз;

в) скачкообразный характер появления новой фазы;

г) взаимное равновесие фаз в промежуточных состояниях фазового перехода;

д) существование метастабильных состояний типа перегретой жидкости или переохлаждённого пара.

Переход твердого вещества в жидкое (плавление) и обратный переход (кристаллизация) относятся к фазовым переходам первого рода, при которых скачком изменяются плотность, внутренняя энергия, энтропия тела. При этом поглощается (при плавлении) или выделяется (при кристаллизации) энергия, называемая теплотой плавления (кристаллизации).

Т,К Тк 0 t,с

При заданном давлении прямое и обратное фазовые превращения происходят при строго определенной температуре, поэтому изобарный фазовый переход одновременно является изотермическим. Одним из возможных способов измерения температуры и теплоты кристаллизации является метод построения диаграммы отвердевания(или плавления),т.е. кривой зависимости температуры отвердевающего (или расплавляемого) вещества от времени при неизменных внешних условиях.

Рис. 1

Для получения диаграммы, сосуд (ампулу) c исследуемым веществом помещают в печь и, нагревая его, измеряют через определенные промежутки времени температуру вещества в ампуле.

На диаграмме отвердевания (рис.1) качественно изображен процесс медленного охлаждения и кристаллизации металлической пробы (олово), помещенной в нагреваемую ампулу. При достаточно медленном охлаждении можно считать, что температуры Т пробы и ампулы одинаковы во всех точках. Эта температура отмечается по вертикальной оси диаграммы. Если тепловая мощность N, отдаваемая образцом, может считаться постоянной, то горизонтальная ось времени (рис.1) является одновременно и осью “теплоты, отданной образцом и ампулой”. Тепловая мощность N не равна мощности нагревателя, т.к. часть теплоты отводится в окружающую среду.

Левая и правая убывающие части кривой на рис.1 изображают остывание расплава и ампулы (слева) и остывание твердого образца и ампулы (справа). Тепловая мощность N на любом из этих участков равна изменению внутренней энергии системы за единицу времени:

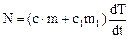(1)

Массы пробы металла m и ампулы m₁ , а также их удельные теплоемкости с и c₁ вблизи температуры плавления известны. Горизонтальный участок на рис.1 изображает процесс кристаллизации металла. Ордината его - температура плавления, а приращение абсциссы - время фазового перехода t_ф.п. Здесь выполняется равенство:

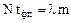, (2)

где l - удельная теплота кристаллизации. Исключив N из формул (1) и (2), найдем:

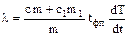, (3)

где - скорость охлаждения образца.

Любое изменение состояния системы в общем случае можно представить как результат бесконечно большого числа бесконечно малых изменений. Величина, равная отношению теплоты, полученной телом при изотермическом процессе, к температуре, при которой происходит теплопередача, т.е. Q/T, называется приведенной теплотой. 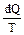Приведенное количество теплоты, сообщаемое телу на бесконечно малом участке процесса равно .Для обратимых процессов , следовательно, есть полный дифференциал некоторой функции, не зависящий от пути, каким система пришла в данное состояние.

Функция состояния системы, характеризующая направление протекания самопроизвольных процессов в замкнутой термодинамической системе, называется энтропией, дифференциалом которой является выражение :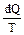

(4)

Если система перешла из состояния 1 в состояние 2, имеет смысл говорить только об увеличении или уменьшении энтропии системы, т.е. об её изменении:

DS =S₂ - S₁=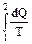

В замкнутых системах энтропия может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов):

DS ³ 0 (5)

Так как реальные процессы необратимы, то все процессы в замкнутой системе ведут к увеличению энтропии.

Также как и внутренняя энергия, энтропия обладает свойством аддитивности и является однозначной функцией состояния термодинамической системы.

Физический смысл энтропии был выяснен Больцманом, который связал энтропию с термодинамической вероятностью состояния системы W:

S =k lnW, (6)

где k - постоянная Больцмана.

Термодинамическая вероятность W состояния системы - это число способов, которыми может быть реализовано данное состояние макроскопической системы, или число микросостояний, осуществляющих данное макросостояние (по определению W³1).

Таким образом, энтропия определяется логарифмом статистического веса данной системы. Статистическим весом (или термодинамической вероятностью) системы называют число микроскопических (молекулярных) способов, с помощью которых может быть реализованно данное макросостояние этой системы. Следовательно, энтропия может рассматриваться как мера вероятности состояния термодинамической системы. Её статистическое толкование следующее:энтропия - мера молекулярного беспорядка в системе или мера неупорядоченности системы. Используя понятие энтропии, Больцман дал свою формулировку второго закона термодинамики: «Все процессы в природе протекают в направлении, приводящем к увеличению вероятности состояния».

При плавлении телу нужно сообщить некоторое количество теплоты, чтобы вызвать разрушение кристаллической решетки. Подводимая при плавлении теплота идет не на нагрев тела, а на разрыв межатомных связей, поэтому плавление протекает при постоянной температуре. При подобных переходах - из более упорядоченного кристаллического состояния в менее упорядоченное жидкое состояние - степень беспорядка увеличивается и, с точки зрения второго начала термодинамики, этот процесс связан с возрастанием энтропии системы. Если переход происходит в обратном направлении (кристаллизация), то система теплоту выделяет и энтропия системы убывает.

При процессе кристаллизации выделяется количество теплоты:

DQ = l × m (7)

Тогда, используя формулу (4), имеем выражения для изменения энтропии DS в процессе кристаллизации:

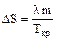, (8)

где Т_кр - температура кристаллизации.