 Эффект Комптона.Распространяясь в веществе,
Эффект Комптона.Распространяясь в веществе, 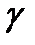 -излучение взаимодействует с электронами и ядрами атомов, а также с кулоновским полем, окружающим ядра и электроны атомов. Имеется возможность осуществления более десятка элементарных процессов взаимодействия
-излучение взаимодействует с электронами и ядрами атомов, а также с кулоновским полем, окружающим ядра и электроны атомов. Имеется возможность осуществления более десятка элементарных процессов взаимодействия 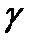 -излучения с веществом, заканчивающихся поглощением или рассеянием
-излучения с веществом, заканчивающихся поглощением или рассеянием 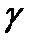 -квантов.В качестве примера взаимодействия фотона с частицами вещества рассмотрим упругое рассеяние фотона на первоначально покоящейся частице (электроне) – эффект Комптона.Упругое рассеяние фотона на первоначально покоящемся электроне приводит к изменению длины волны фотона и появлению электрона отдачи – так называется электрон, получивший импульс в результате реакции. Атомарный электрон в этом случае можно рассматривать как свободную частицу, так как при комптоновском рассеянии энергия фотона значительно превышает энергию связи электрона в атоме.Пусть фотон с длиной волны
-квантов.В качестве примера взаимодействия фотона с частицами вещества рассмотрим упругое рассеяние фотона на первоначально покоящейся частице (электроне) – эффект Комптона.Упругое рассеяние фотона на первоначально покоящемся электроне приводит к изменению длины волны фотона и появлению электрона отдачи – так называется электрон, получивший импульс в результате реакции. Атомарный электрон в этом случае можно рассматривать как свободную частицу, так как при комптоновском рассеянии энергия фотона значительно превышает энергию связи электрона в атоме.Пусть фотон с длиной волны 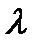 рассеивается под углом
рассеивается под углом  на покоящемся электроне. При этом длина волны рассеянного фотона
на покоящемся электроне. При этом длина волны рассеянного фотона 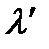 , а электрон отдачи вылетает под углом
, а электрон отдачи вылетает под углом  к направлению распространения падающего фотона. Найдем изменение длины волны
к направлению распространения падающего фотона. Найдем изменение длины волны 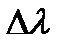 фотона при комптоновском рассеянии.Для данного случая запишем закон сохранения импульса:
фотона при комптоновском рассеянии.Для данного случая запишем закон сохранения импульса: 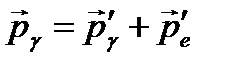 ,где
,где 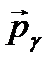 и
и 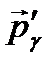 − импульсы падающего и рассеянного фотонов,
− импульсы падающего и рассеянного фотонов,  − импульс электрона отдачи (частицы отдачи) и закон сохранения энергии:
− импульс электрона отдачи (частицы отдачи) и закон сохранения энергии:  ,где
,где 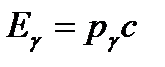 и
и 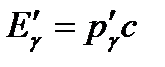 − энергии падающего и рассеянного фотонов,
− энергии падающего и рассеянного фотонов,  − полная энергия электрона отдачи (частицы отдачи),
− полная энергия электрона отдачи (частицы отдачи), 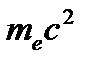 − энергия покоя электрона,
− энергия покоя электрона, 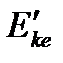 − кинетическая энергия электрона после рассеяния.Используя векторную диаграмму для импульсов взаимодействующих частиц, перейдем от векторной формы записи закона сохранения импульса (4.1) к скалярной форме, используя теорему косинусов:
− кинетическая энергия электрона после рассеяния.Используя векторную диаграмму для импульсов взаимодействующих частиц, перейдем от векторной формы записи закона сохранения импульса (4.1) к скалярной форме, используя теорему косинусов: 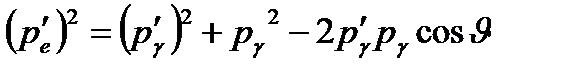 .Тогда уравнения (4.2) и (4.3) можно записать в виде системы:
.Тогда уравнения (4.2) и (4.3) можно записать в виде системы: 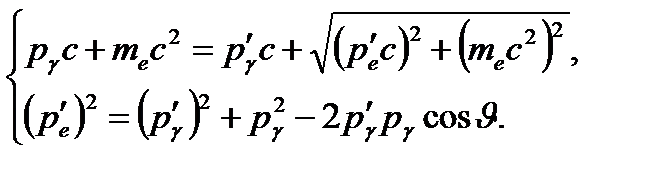
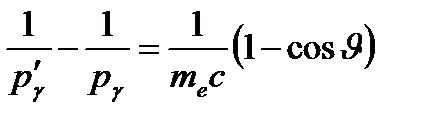 ,Учтем, что
,Учтем, что 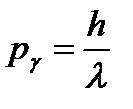 и
и 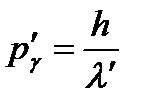 , и выразим изменение длины волны фотона при рассеянии:
, и выразим изменение длины волны фотона при рассеянии: 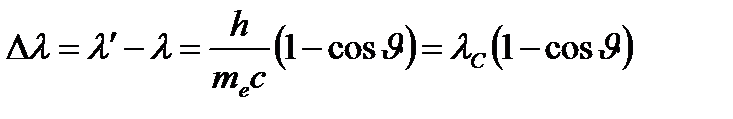 ,где
,где 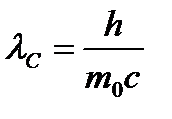 – комптоновская длина волны частицы с массой покоя
– комптоновская длина волны частицы с массой покоя 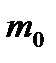 . (Для электрона комптоновская длина волны
. (Для электрона комптоновская длина волны  м, для протона
м, для протона 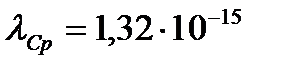 м.).Энергия рассеянного фотона равна
м.).Энергия рассеянного фотона равна 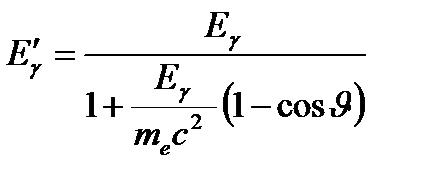
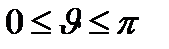
| Рис. 1. К эффекту Комптона |
Энергию электрона отдачи (частицы отдачи) можно выразить через угол рассеяния фотона
:
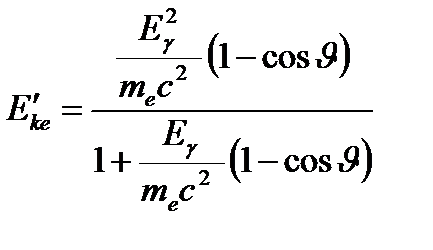
или через угол рассеяния

самого электрона:
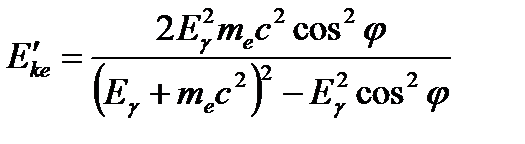
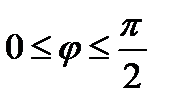
Связь между углами рассеяния:
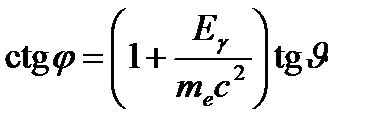
. Изменение длины волны фотона при комптоновском рассеянии не зависит от самой длины волны

(и соответственно, энергии
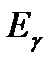
) падающего фотона, а определяется только углом рассеяния фотона
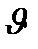
. Фотоны, рассеянные на углы
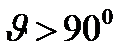
, всегда имеют энергию

МэВ независимо от начальной энергии
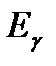
, а при
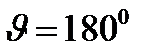
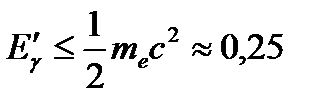
МэВ. При рассеянии назад (
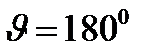
,

) фотон уносит минимальную энергию:
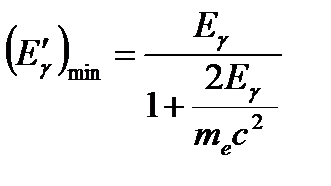
, при этом кинетическая энергия комптоновского электрона максимальна:
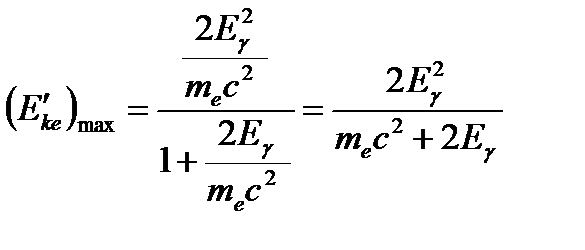
. Упругое рассеяние фотона на первоначально покоящейся частице приводит к изменению его длины волны и появлению т.н. частицы отдачи – так называется частица, получившая импульс в результате реакции.
Рассмотрим процесс упругого столкновения фотонов со свободными электронами (свободными можно считать электроны, энергии связи которых в атоме значительно меньше той энергии, которую фотон может передать электрону при взаимодействии). Пусть на первоначально покоившийся электрон падает фотон с энергией 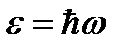 и импульсом
и импульсом 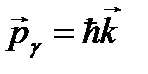 . Энергия электрона до столкновения равна его энергии покоя
. Энергия электрона до столкновения равна его энергии покоя 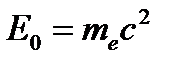 , импульс электрона
, импульс электрона 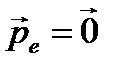 . После столкновения электрон будет обладать импульсом
. После столкновения электрон будет обладать импульсом  и энергией
и энергией 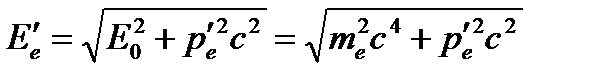 . Энергия и импульс фотона также изменятся и станут равными
. Энергия и импульс фотона также изменятся и станут равными 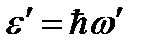 и
и 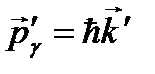 . Из законов сохранения энергии и импульса системы следуют два равенства:
. Из законов сохранения энергии и импульса системы следуют два равенства:  ,
, 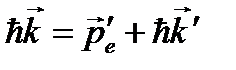 . Длина волны рассеянного фотона оказывается большей исходной его длины волны на величину
. Длина волны рассеянного фотона оказывается большей исходной его длины волны на величину 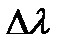 , называемую комптоновским смещением длины волны рассеянного фотона:
, называемую комптоновским смещением длины волны рассеянного фотона: 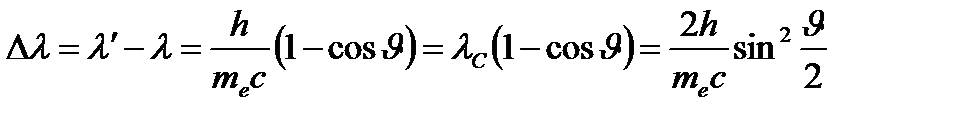 , где J – угол рассеяния фотона в лабораторной системе отсчета (угол между векторами
, где J – угол рассеяния фотона в лабораторной системе отсчета (угол между векторами 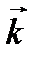 и
и 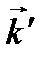 , рис. 1); величина
, рис. 1); величина 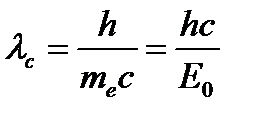 называется комптоновской длиной волны электрона (частицы). Для электрона и протона ее значения примерно равны соответственно λce 2,43×10-12 м, λcp 1,32×10-15 м. Энергия рассеянного фотона
называется комптоновской длиной волны электрона (частицы). Для электрона и протона ее значения примерно равны соответственно λce 2,43×10-12 м, λcp 1,32×10-15 м. Энергия рассеянного фотона 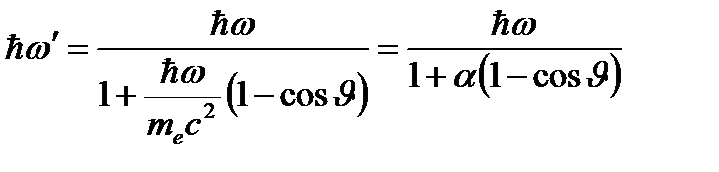 , где
, где 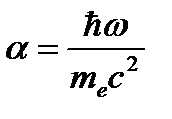 . Кинетическая энергия электрона (частицы) отдачи
. Кинетическая энергия электрона (частицы) отдачи 
13. Виды спектров. Закономерности атомных спектров. Комбинационный принцип Ритца.Виды спектров:1)раскаленные ТВ.тела или жидкости, созд. Непр или сплошные спектры излуч. Пример: ачт,солнце. 2) атомарные газы при высоких Т, созд. Линейчатые спектры испуск., сост.из отдельных узких спектральных линий. В этом сл.атомы можно счит.не взаим.др.сдр.,поэт. Спектры также наз.атомными. Изолир.атомы опр. хим.эл. спектр.линии, присущие только этому хим.эл. 3) молек.газы при высоких Т созд. Полосатые спектры испускания: мн-во тесно располож.линий,обр.группы или полосы, раздел. темными промежутками.Анализ эмпирических данных по линейчатым спектрам показал, что отдельные линии в спектрах могут быть объединены в группы линий, которые принято называть сериями. Бальмер пришел к выводу (1885), что линии в видимой части спектра водорода можно представить следующей формулой: 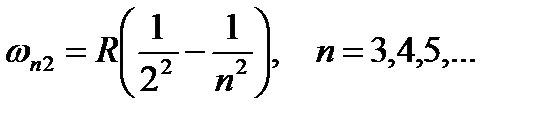 , где
, где  − частота излучения соответствующей линии,
− частота излучения соответствующей линии,  с-1 − постоянная Ридберга. Эта серия линий называется серией Бальмера. Лайман открыл (1906) другую серию линий, лежащую в ультрафиолетовой части спектра атома водорода:
с-1 − постоянная Ридберга. Эта серия линий называется серией Бальмера. Лайман открыл (1906) другую серию линий, лежащую в ультрафиолетовой части спектра атома водорода:  Эта серия называется серией Лаймана. Пашен открыл (1908) серию в инфракрасной части спектра атома водорода:
Эта серия называется серией Лаймана. Пашен открыл (1908) серию в инфракрасной части спектра атома водорода: 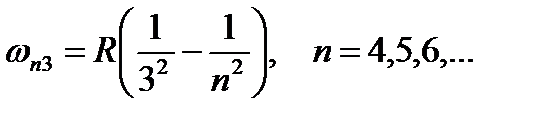 Эта серия называется серией Пашена. В дальнейшем в инфракрасной части спектра водорода были открыты также другие серии: серия Брэкета
Эта серия называется серией Пашена. В дальнейшем в инфракрасной части спектра водорода были открыты также другие серии: серия Брэкета  серия Пфундта
серия Пфундта  Все эти серии можно представить в виде обобщенной формулы Бальмера:
Все эти серии можно представить в виде обобщенной формулы Бальмера:  Комбинационный принцип Ритца (1908): Все многообразие спектральных линий рассматриваемого атома может быть получено путем попарных комбинаций величин называемых спектральными термами
Комбинационный принцип Ритца (1908): Все многообразие спектральных линий рассматриваемого атома может быть получено путем попарных комбинаций величин называемых спектральными термами 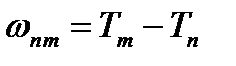 . Для атома водорода спектральные термы можно задать выражением:
. Для атома водорода спектральные термы можно задать выражением: 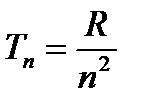 . Серия линий получается, если число
. Серия линий получается, если число  фиксировано,
фиксировано,  пробегает все целые значения
пробегает все целые значения  . Однако не все возможные комбинации спектральных термов атома соответствуют фактически существующим линиям в спектре.
. Однако не все возможные комбинации спектральных термов атома соответствуют фактически существующим линиям в спектре.
 Эффект Комптона.Распространяясь в веществе,
Эффект Комптона.Распространяясь в веществе, 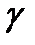 -излучение взаимодействует с электронами и ядрами атомов, а также с кулоновским полем, окружающим ядра и электроны атомов. Имеется возможность осуществления более десятка элементарных процессов взаимодействия
-излучение взаимодействует с электронами и ядрами атомов, а также с кулоновским полем, окружающим ядра и электроны атомов. Имеется возможность осуществления более десятка элементарных процессов взаимодействия 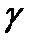 -излучения с веществом, заканчивающихся поглощением или рассеянием
-излучения с веществом, заканчивающихся поглощением или рассеянием 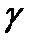 -квантов.В качестве примера взаимодействия фотона с частицами вещества рассмотрим упругое рассеяние фотона на первоначально покоящейся частице (электроне) – эффект Комптона.Упругое рассеяние фотона на первоначально покоящемся электроне приводит к изменению длины волны фотона и появлению электрона отдачи – так называется электрон, получивший импульс в результате реакции. Атомарный электрон в этом случае можно рассматривать как свободную частицу, так как при комптоновском рассеянии энергия фотона значительно превышает энергию связи электрона в атоме.Пусть фотон с длиной волны
-квантов.В качестве примера взаимодействия фотона с частицами вещества рассмотрим упругое рассеяние фотона на первоначально покоящейся частице (электроне) – эффект Комптона.Упругое рассеяние фотона на первоначально покоящемся электроне приводит к изменению длины волны фотона и появлению электрона отдачи – так называется электрон, получивший импульс в результате реакции. Атомарный электрон в этом случае можно рассматривать как свободную частицу, так как при комптоновском рассеянии энергия фотона значительно превышает энергию связи электрона в атоме.Пусть фотон с длиной волны 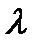 рассеивается под углом
рассеивается под углом  на покоящемся электроне. При этом длина волны рассеянного фотона
на покоящемся электроне. При этом длина волны рассеянного фотона 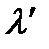 , а электрон отдачи вылетает под углом
, а электрон отдачи вылетает под углом  к направлению распространения падающего фотона. Найдем изменение длины волны
к направлению распространения падающего фотона. Найдем изменение длины волны 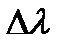 фотона при комптоновском рассеянии.Для данного случая запишем закон сохранения импульса:
фотона при комптоновском рассеянии.Для данного случая запишем закон сохранения импульса: 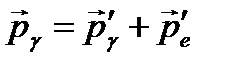 ,где
,где 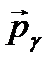 и
и 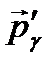 − импульсы падающего и рассеянного фотонов,
− импульсы падающего и рассеянного фотонов,  − импульс электрона отдачи (частицы отдачи) и закон сохранения энергии:
− импульс электрона отдачи (частицы отдачи) и закон сохранения энергии:  ,где
,где 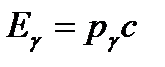 и
и 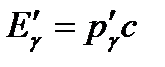 − энергии падающего и рассеянного фотонов,
− энергии падающего и рассеянного фотонов,  − полная энергия электрона отдачи (частицы отдачи),
− полная энергия электрона отдачи (частицы отдачи), 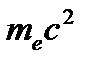 − энергия покоя электрона,
− энергия покоя электрона, 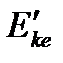 − кинетическая энергия электрона после рассеяния.Используя векторную диаграмму для импульсов взаимодействующих частиц, перейдем от векторной формы записи закона сохранения импульса (4.1) к скалярной форме, используя теорему косинусов:
− кинетическая энергия электрона после рассеяния.Используя векторную диаграмму для импульсов взаимодействующих частиц, перейдем от векторной формы записи закона сохранения импульса (4.1) к скалярной форме, используя теорему косинусов: 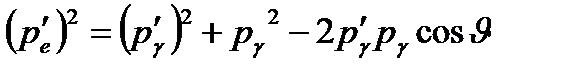 .Тогда уравнения (4.2) и (4.3) можно записать в виде системы:
.Тогда уравнения (4.2) и (4.3) можно записать в виде системы: 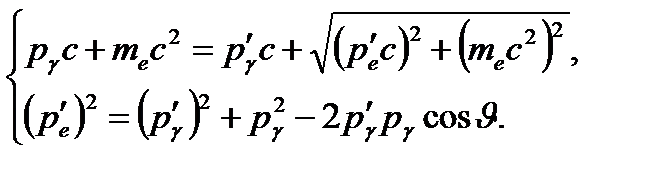
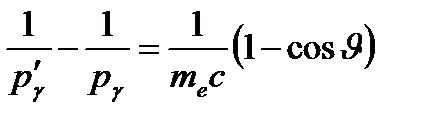 ,Учтем, что
,Учтем, что 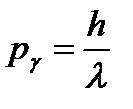 и
и 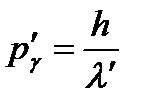 , и выразим изменение длины волны фотона при рассеянии:
, и выразим изменение длины волны фотона при рассеянии: 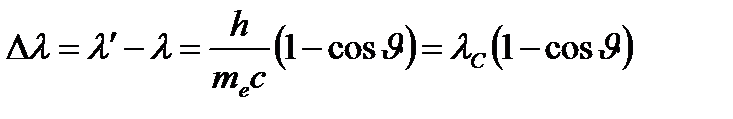 ,где
,где 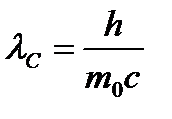 – комптоновская длина волны частицы с массой покоя
– комптоновская длина волны частицы с массой покоя 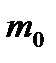 . (Для электрона комптоновская длина волны
. (Для электрона комптоновская длина волны  м, для протона
м, для протона 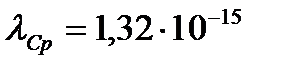 м.).Энергия рассеянного фотона равна
м.).Энергия рассеянного фотона равна 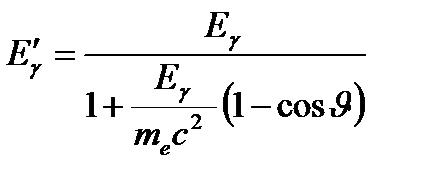
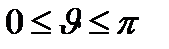
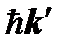
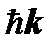
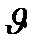 :
: 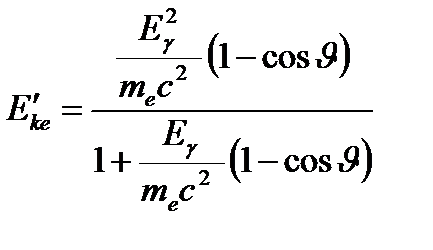 или через угол рассеяния
или через угол рассеяния  самого электрона:
самого электрона: 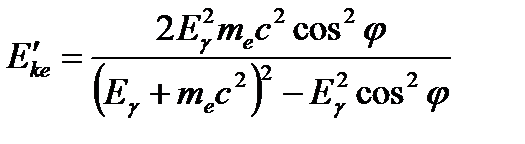
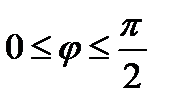 Связь между углами рассеяния:
Связь между углами рассеяния: 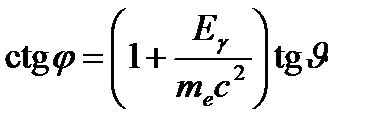 . Изменение длины волны фотона при комптоновском рассеянии не зависит от самой длины волны
. Изменение длины волны фотона при комптоновском рассеянии не зависит от самой длины волны  (и соответственно, энергии
(и соответственно, энергии 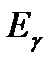 ) падающего фотона, а определяется только углом рассеяния фотона
) падающего фотона, а определяется только углом рассеяния фотона 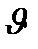 . Фотоны, рассеянные на углы
. Фотоны, рассеянные на углы 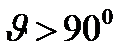 , всегда имеют энергию
, всегда имеют энергию  МэВ независимо от начальной энергии
МэВ независимо от начальной энергии 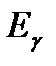 , а при
, а при 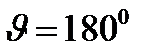
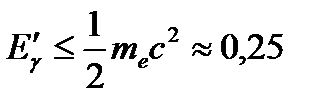 МэВ. При рассеянии назад (
МэВ. При рассеянии назад ( 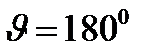 ,
,  ) фотон уносит минимальную энергию:
) фотон уносит минимальную энергию: 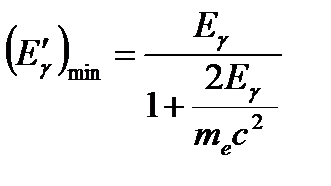 , при этом кинетическая энергия комптоновского электрона максимальна:
, при этом кинетическая энергия комптоновского электрона максимальна: 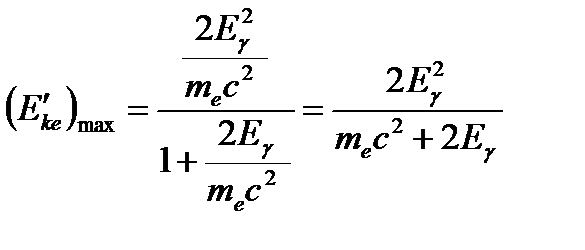 . Упругое рассеяние фотона на первоначально покоящейся частице приводит к изменению его длины волны и появлению т.н. частицы отдачи – так называется частица, получившая импульс в результате реакции.
. Упругое рассеяние фотона на первоначально покоящейся частице приводит к изменению его длины волны и появлению т.н. частицы отдачи – так называется частица, получившая импульс в результате реакции. 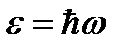 и импульсом
и импульсом 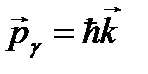 . Энергия электрона до столкновения равна его энергии покоя
. Энергия электрона до столкновения равна его энергии покоя 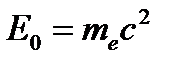 , импульс электрона
, импульс электрона 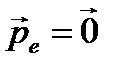 . После столкновения электрон будет обладать импульсом
. После столкновения электрон будет обладать импульсом  и энергией
и энергией 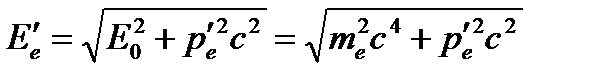 . Энергия и импульс фотона также изменятся и станут равными
. Энергия и импульс фотона также изменятся и станут равными 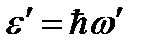 и
и 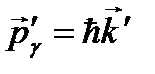 . Из законов сохранения энергии и импульса системы следуют два равенства:
. Из законов сохранения энергии и импульса системы следуют два равенства:  ,
, 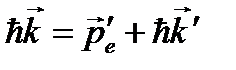 . Длина волны рассеянного фотона оказывается большей исходной его длины волны на величину
. Длина волны рассеянного фотона оказывается большей исходной его длины волны на величину 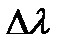 , называемую комптоновским смещением длины волны рассеянного фотона:
, называемую комптоновским смещением длины волны рассеянного фотона: 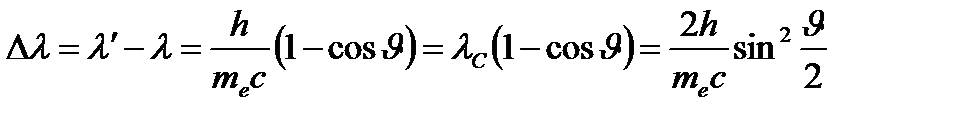 , где J – угол рассеяния фотона в лабораторной системе отсчета (угол между векторами
, где J – угол рассеяния фотона в лабораторной системе отсчета (угол между векторами 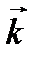 и
и 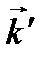 , рис. 1); величина
, рис. 1); величина 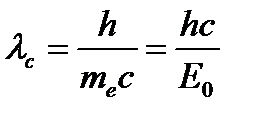 называется комптоновской длиной волны электрона (частицы). Для электрона и протона ее значения примерно равны соответственно λce 2,43×10-12 м, λcp 1,32×10-15 м. Энергия рассеянного фотона
называется комптоновской длиной волны электрона (частицы). Для электрона и протона ее значения примерно равны соответственно λce 2,43×10-12 м, λcp 1,32×10-15 м. Энергия рассеянного фотона 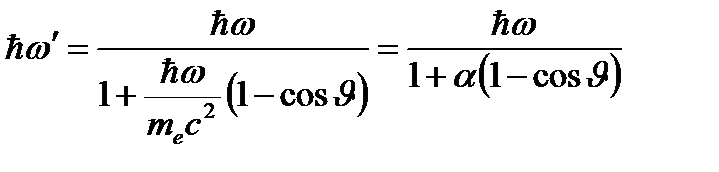 , где
, где 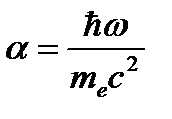 . Кинетическая энергия электрона (частицы) отдачи
. Кинетическая энергия электрона (частицы) отдачи 
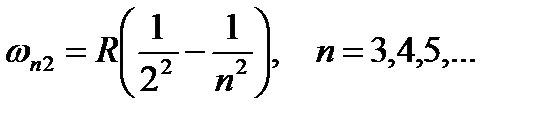 , где
, где  − частота излучения соответствующей линии,
− частота излучения соответствующей линии,  с-1 − постоянная Ридберга. Эта серия линий называется серией Бальмера. Лайман открыл (1906) другую серию линий, лежащую в ультрафиолетовой части спектра атома водорода:
с-1 − постоянная Ридберга. Эта серия линий называется серией Бальмера. Лайман открыл (1906) другую серию линий, лежащую в ультрафиолетовой части спектра атома водорода:  Эта серия называется серией Лаймана. Пашен открыл (1908) серию в инфракрасной части спектра атома водорода:
Эта серия называется серией Лаймана. Пашен открыл (1908) серию в инфракрасной части спектра атома водорода: 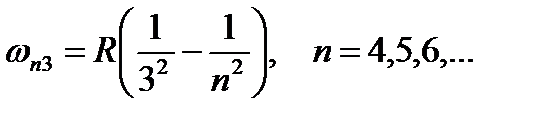 Эта серия называется серией Пашена. В дальнейшем в инфракрасной части спектра водорода были открыты также другие серии: серия Брэкета
Эта серия называется серией Пашена. В дальнейшем в инфракрасной части спектра водорода были открыты также другие серии: серия Брэкета  серия Пфундта
серия Пфундта  Все эти серии можно представить в виде обобщенной формулы Бальмера:
Все эти серии можно представить в виде обобщенной формулы Бальмера:  Комбинационный принцип Ритца (1908): Все многообразие спектральных линий рассматриваемого атома может быть получено путем попарных комбинаций величин называемых спектральными термами
Комбинационный принцип Ритца (1908): Все многообразие спектральных линий рассматриваемого атома может быть получено путем попарных комбинаций величин называемых спектральными термами 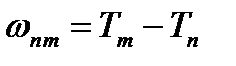 . Для атома водорода спектральные термы можно задать выражением:
. Для атома водорода спектральные термы можно задать выражением: 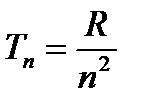 . Серия линий получается, если число
. Серия линий получается, если число  фиксировано,
фиксировано,  пробегает все целые значения
пробегает все целые значения  . Однако не все возможные комбинации спектральных термов атома соответствуют фактически существующим линиям в спектре.
. Однако не все возможные комбинации спектральных термов атома соответствуют фактически существующим линиям в спектре.