Дополнительные приложения квантовой механики

Прохождение частицы через потенциальный барьер.

Туннельный эффект

Рассмотрим движение частицы при прохождении потенциального барьера. Пусть она движется слева направо и встречает на своем пути потенциальный барьер высотой U₀ и шириной l (рис. 6.1). Согласно классической теории, если энергия частицы больше высоты барьера (E > U₀), то она беспрепятственно пройдет над барьером.

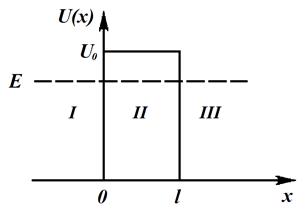
Рис. 6.1. Потенциальный барьер

При этом скорость частицы несколько снизится в области II и примет первоначальное значение в области III. Если же энергия частицы меньше высоты барьера (E < U₀), то сквозь барьер она проникнуть не сможет, поэтому отразится от стенки барьера и полетит в обратном направлении.

Квантовая механика предсказывает иное поведение частицы. В частности, даже если E>U₀, существует ненулевая вероятность, что частица отразится от барьера и полетит в обратную сторону. В тоже время частица может проникнуть сквозь барьер независимо от того, превышает ли ее энергия величину потенциального барьера или нет.

Рассмотрим ситуацию, когда E<U₀, в этом случае уравнение Шредингера:

для областей I и III имеет вид: 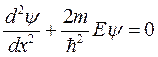(6.1)

а для области II: 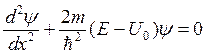(6.2)

Решениями этих уравнений будут функции ψ₁(x), ψ₂(x), ψ₃(x), что легко проверить подстановкой: Вид этих функций представлен на рис. 6.2.

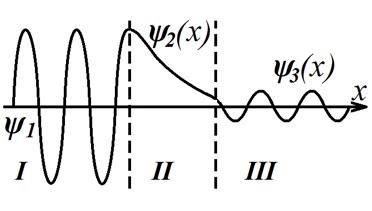
Рис. 6.2. Изменение волновой функции при переходе через потенциальный барьер

Запишем их:

для области I: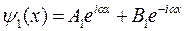

для области III: 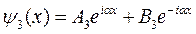где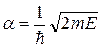

для области II: 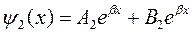где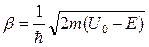

Слагаемое в каждом решении вида е^iαx соответствует волне, распространяющейся в положительном направлении оси x, слагаемое же вида е^–iαx соответствует волне, распространяющейся в отрицательном направлении оси x.

Сразу отметим, что коэффициент В₃ должен быть равен нулю, так как в области III есть только волна, распространяющаяся в положительном направлении оси x, то есть слева направо. Для нахождения остальных коэффициентов необходимо воспользоваться упомянутыми выше условиями, накладываемыми на волновую функцию – однозначность, непрерывность и конечность.

Чтобы функция была непрерывна, волновые функции на границах рассматриваемых областей должны иметь одинаковое значение:

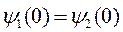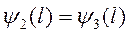и (6.3)

чтобы ψ была гладкой (без изломов), ее производные должны быть непрерывны на границах областей:

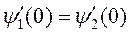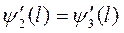и (6.4)

Отсюда вытекают уравнения на искомые коэффициенты:

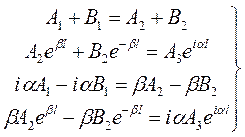(6.5)

Решение этой системы {А₁, А₂, А₃, В₁ и В₂} позволяет найти две важные величины: вероятность отражения частицы от потенциального барьера: 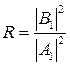, называемую коэффициентом отражения, а также вероятность прохождения частицы через барьер: 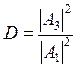, называемую коэффициентом прохождения (или коэффициентом прозрачности). Коэффициенты R и D связаны соотношением: 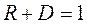(6.6)

Можно показать, что 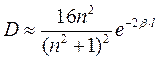, где .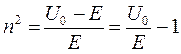

Поскольку выражение 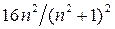имеет величину порядка единицы, то коэффициент прозрачности можно считать равным:

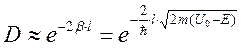(6.7)

Для потенциального барьера произвольной формы (рис. 6.3) формула 6.7 заменяется выражением:

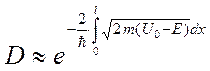(6.8)

При преодолении барьера частица как бы проходит через «туннель» в барьере (заштрихованная область на рис. 6.3). В связи с этим явление прохождения квантовых частиц сквозь непреодолимые с классической точки зрения препятствия названо туннельным эффектом.

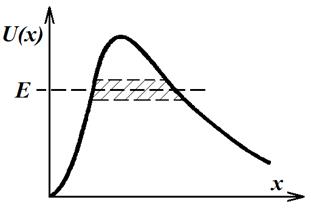
Рис. 6.3. Туннель в потенциальном барьере произвольной формы

Классическая физика не может допустить существования туннельного эффекта. Например, пусть тело без трения скользит и встречает на своем пути горку высотой h (чем выше горка, тем больше потенциальный барьер). Если тело имеет заданную кинетическую энергию, и эта энергия меньше, чем по закону сохранения требуется для преодоления горки, то есть mV²/2 ˂ mgh. В этом случае тело поднимется до той высоты, где вся его кинетическая энергия перейдет в потенциальную, остановится, а затем начнет движение в обратном направлении.

Для частиц, имеющих квантовые свойства, туннельный эффект наблюдается очень часто. Например, α-частица, покидающая ядро при α-распаде полония ²¹⁰Po, преодолевает потенциальный барьер U = 23 МэВ, величина которого существенно превосходит энергию самой α-частицы E_α = 5.3 МэВ. То есть, не будь возможен в этом случае туннельный эффект, α-излучения бы не существовало. Также не было бы возможным простое протекание тока через окисленный контакт (например, через вилку, вставляемую в розетку), так как тонкий не заметный для глаза слой окисла на поверхности металла создает потенциальный барьер. Большинство электронов имеют энергию гораздо меньше величины этого барьера, что является существенным затруднением для их движения.