Нормальное распределение Гаусса

При 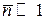и относительно малом отклонении от среднего 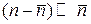выполняется нормальное распределение

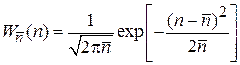. (1.19)

Резултат получил Гаусс в 1809 г.

Карл Фридрих Гаусс (1777–1855)

Доказательство:

Распределение Пуассона

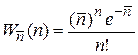
логарифмируем

.

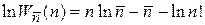Используем формулу Стирлинга (будет доказана в курсе ММФ)

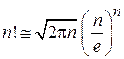, при ,

,

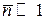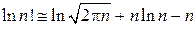тогда

.

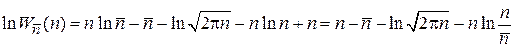Учитывая

, ,

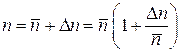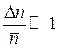разлагаем в ряд

.

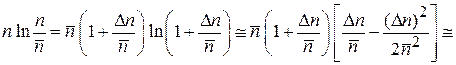
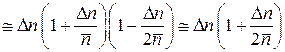В результате

.

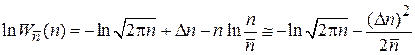Заменяя 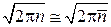и потенцируя, получаем (1.19).

Условие нормировки

На основании 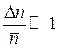считаем n квазинепрерывным, тогда

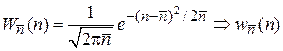– плотность вероятности,

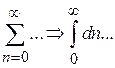
Условие нормировки получает вид

,

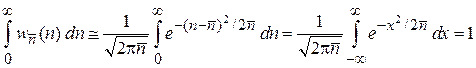где

;

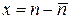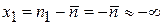при ;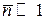

;

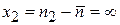учтено

.

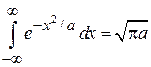Среднее значение

,

,

,

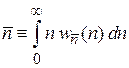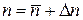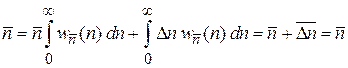где

.

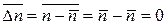Дисперсия

,

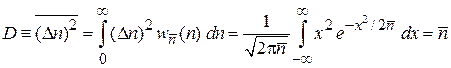где

, ,

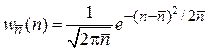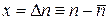и учтено

.

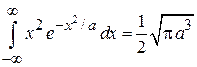В результате

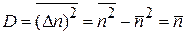. (1.20)

Из (1.19) и (1.20) плотность вероятности

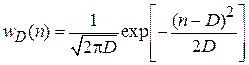. (1.21)

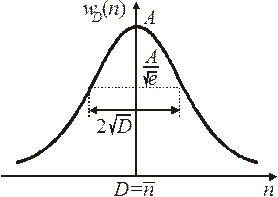
Распределение Гаусса,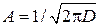

Центральная предельная теорема – при суммировании большого числа независимых случайных величин, имеющих различные распределения, результирующее распределение близко к распределению Гаусса.

Теорема обосновывает применимость нормального распределения к многочисленным случайным процессам. Теорему доказал Ляпунов в 1901 г.

Александр Михайлович Ляпунов (1857–1918)

ПРОИЗВОДЯЩАЯ ФУНКЦИЯ

Производящая функция позволяет получать важные соотношения теории вероятности простым путем.

Для дискретного распределения 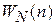случайной величины n ( 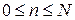) определяем производящую функцию

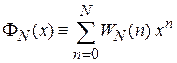, (1.22)

где |x| £ 1 обеспечивает сходимость сумма. Из (1.22) получаем функцию распределения

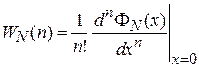. (1.23)

Средние значения и дисперсия

Используем

,

,

.

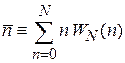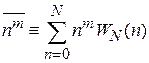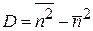Из (1.22) находим

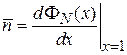, (1.24)

,

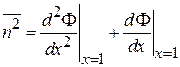ПРИМЕРЫ

1.Для распределения Пуассона найти производящую функцию и .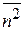

Используем производящую функцию (П.1.5) для биномиального распределения (см. практические занятия)

,

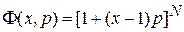и

,

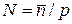тогда

.

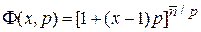Учитываем 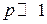, тогда

, .

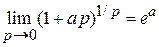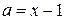Получаем производящую функцию распределения Пуассона

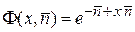. (П.1.14)

Из (1.25)

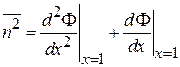
с учетом

, ,

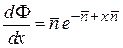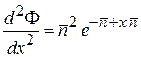следует (1.20)

.

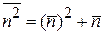2.Найти распределение времен свободного пробега электрона металла.

Согласно классической теории в узлах кристаллической решетки металла находятся ионы, валентные электроны образуют идеальный газ. Любой макроскопический объем металла электрически нейтрален, поэтому на электрон не действуют электростатические силы и благодаря тепловому движению он свободно перемещается от одного столкновения с ионом до следующего.

При термодинамическом равновесии тепловые процессы стационарные и вероятность b столкновения электрона за единицу времени не зависит от t. Вероятность столкновения за время dt равна

.

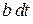Функция распределения времен свободного пробега w(t) равна вероятности того, что время свободного движения лежит в единичном интервале около значения t.

Вероятность независимых событий – свободного движения электрона до момента t и столкновения в следующий промежуток dt, равна

,

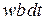и является уменьшением вероятности обнаружения электрона при переходе от t к 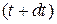. В результате

.

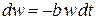Разделяя переменные и интегрируя

,

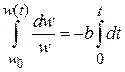получаем

,

.

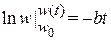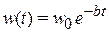Условие нормировки

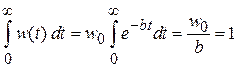
дает

, .

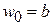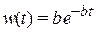Среднее время свободного пробега

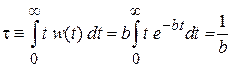. (П.1.22)

В результате функция распределения времен свободного пробега

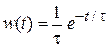. (П.1.23)

Вероятность свободного движения в течение времени t уменьшается экспоненциально с ростом t. Среднеквадратичное время свободного пробега

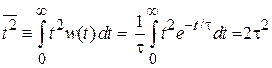(П.1.23а)

равно удвоенному квадрату среднего времени свободного пробега.

3.Найти скорость дрейфа 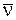электронов металла в электрическом поле Е.

За время свободного пробега t электрон набирает скорость 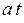, где ускорение 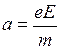. Если при столкновении упорядоченная скорость теряется, то средняя скорость

.

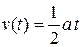Время свободного пробега меняется от столкновения к столкновению. Пусть электрон испытывает последовательно N столкновений с временами свободного пробега t₁, t₂,…, t_N и средними скоростями 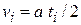, тогда скорость дрейфа

.

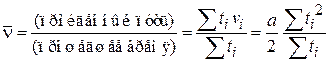Поделив числитель и знаменатель на N, и полагая 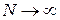, получаем

.

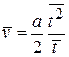Из распределения (П.1.23) 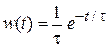находим

, .

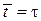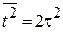Получаем

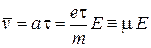, (П.1.24)

где подвижность электронов

.

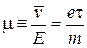Скорость дрейфа пропорциональна электрическому полю и среднему времени t свободного пробега электрона.

1.3. Частицы совершают броуновское движение в жидкости с коэффициентом вязкого трения g при температуре Т. Доказать формулу Эйнштейна (1905 г.) для среднего квадрата смещения частицы вдоль оси x за время t

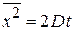, (П.1.25)

где 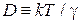– диффузионная постоянная.

На частицу в жидкости действует сила трения

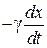
где 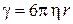– коэффициент вязкого трения для шарообразной частицы радиусом r, η – динамическая вязкость. При соударении с молекулой жидкости действует сила f. Из второго закона Ньютона получаем уравнение движения частицы массой m

.

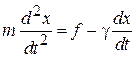Умножаем уравнение на x и используем

,

,

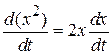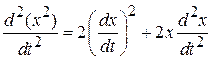и получаем

.

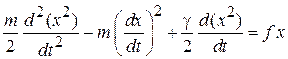Усредняем слагаемые по большому числу частиц, тогда

, , .

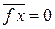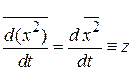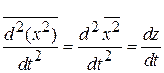Теорема о распределении тепловой энергии (2.40) дает

.

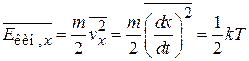Уравнение получает вид

,

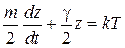или

,

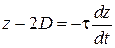где 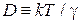– диффузионная постоянная; 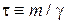– время релаксации. Интегрируем

, ,

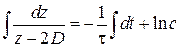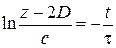находим

,

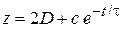где второе слагаемое описывает процесс релаксации. При 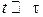пренебрегаем вторым слагаемым и получаем

.

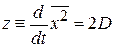Интегрирование дает (П.1.25) .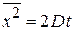

Приведенный вывод предложил Поль Ланжевен в 1908 г. На основе (П.1.25) Жан Перрен измерил постоянную Больцмана и получил число Авогадро в 1926 г. Существенное влияние на броуновское движение оказывает также вихревое течение жидкости, увлекаемой движением частицы, что усложняет формулу (П.1.25), как показали В. Владимирский и Ю.А. Терлецкий в 1945 г. Этим эффектом можно пренебречь для броуновского движения в газе.

При баллистическом движении пройденный частицей путь 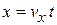, тогда 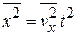. Энергия движения определяется температурой согласно (2.40) 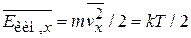, откуда 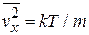. В результате средний квадрат смещения частицы вдоль оси x при 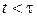пропорционален квадрату времени

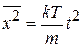. (П.1.26)

Например, кварцевый шарик диаметром 1 мкм, совершающий броуновское движение в воде при комнатной температуре, проходит путь 1 нм за время ~ 1 мкс. Между двумя рассеяниями шарик движется баллистически на протяжении ~ 1Å в течение время ~ 100 нс.