Передача электромагнитной энергии вдоль проводов линии

Передача электромагнитной энергии вдоль проводов линии осуществляется электромагнитным полем, распространяющимся в окружающем провода пространстве. Провода осуществляют роль направляющих электромагнитного поля.

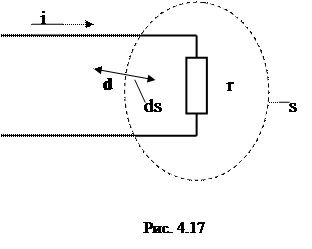
Рассмотрим произвольный приемник электромагнитной энергии, который соединен с источником посредством двухпроводной линией связи. Окружим этот приемник вместе с частью линии замкнутой поверхностью s (рис. 4.17). Предполагая, что в пространстве, в котором расположены провода линии и сам приемник нет свободных зарядов, перепишем уравнение (4.7) в следующем виде:

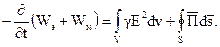
Если мы рассматриваем источник, заключенный внутри поверхности s, то вектор ds имеет направление, совпадающее с внешней нормалью к этой поверхности. Если же мы хотим считать положительной энергию, передаваемую внутрь данной области сквозь поверхность s, то необходимо изменить направление положительной нормали на обратное. В данном случае в последнем выражении следует заменить ds на ds₁

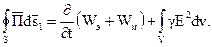
Отсюда видно, что приращение энергии электрического и магнитного полей в объеме V и поглощение энергии в приемнике и в проводах линии, расположенных в этом объеме, происходит за счет передачи энергии в область V сквозь ограничивающую ее поверхность s.

В частном случае, когда ток в цепи постоянный

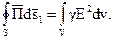
Таким образом, при постоянном токе (все величины неизменны во времени) энергия, поглощаемая в цепи в форме тепла, равна энергии, передаваемой в область V сквозь ограничивающую ее поверхность s.

4.7. Примеры по расчету электромагнитного поля

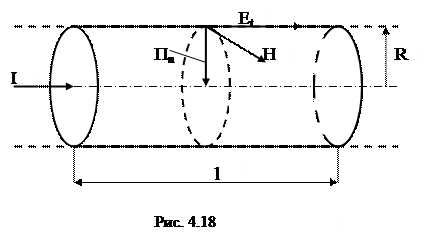
Пример 1. По прямолинейному медному проводу кругового сечения радиусом R = 20 мм (рис. 4.18) протекает постоянный ток I = 6283 А. Определить поток электромагнитной энергии, проникающей в провод на отрезке l = 1 м со стороны внешней среды.

Решение. В начале, используя закон полного тока, найдем напряженность магнитного поля Н на поверхности провода

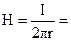50000 А/м

После этого находим касательную составляющую напряженности электрического поля

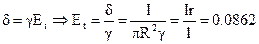В/м.

Здесь удельная проводимость меди g принята равной 58×10⁶ См/м; r – сопротивление отрезка провода длиной l.

Нормальная составляющая вектора Пойнтинга равна:

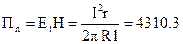Вт/м².

Величина 2pRl = s есть цилиндрическая поверхность данного отрезка провода. Мощность, передаваемая в провод сквозь его поверхность из окружающей среды, оказывается равной:

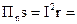541.6 Вт

Отсюда видно, что мощность, передаваемая в провод сквозь его поверхность, полностью расходуется на тепловые потери (I²r).

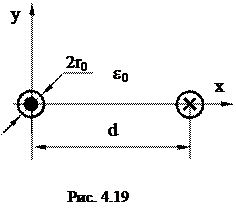Пример 2. По двухпроводной линии постоянного тока (рис. 4.19) передается энергия от генератора к приемнику. Расстояние между осями проводов d = 10 м. Провода выполнены из меди и имеют радиус r₀ = 20 мм. Напряжение между проводами U = =1500 кВ. В линии протекает ток I = 4 кА. Относительное значение диэлектрической проницаемости окружающей среды равно 1. Найти распределение вектора Пойнтинга вдоль линии, соединяющей оси проводов (вдоль оси х). Построить график этого распределения. (Сопротивление проводов при расчете не учитывать).

Решение. Поскольку сопротивление проводов не учитывается, то на оси ох напряженность электрического поля имеет только одну составляющую Е_х. Эта составляющая легко определяется на основе теоремы Гаусса (как было показано в разделе 1). Так, если не учитывать смещение электрических осей проводов (поскольку их радиус гораздо меньше расстояния между ними), то напряженность поля на линии, соединяющей оси проводов (вне проводов), равна:

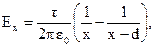
где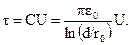

Напряженность магнитного поля на этой линии имеет также одну составляющую, направленную вдоль оси оу, которая определяется с помощью закона полного тока

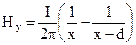
Таким образом, вектор Пойнтинга в области вне проводов на линии, соединяющей оси проводов, имеет одну составляющую, направленную вдоль оси оz

.

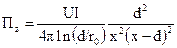Изменение данной составляющей вдоль оси ох показано на рис. 4.20.

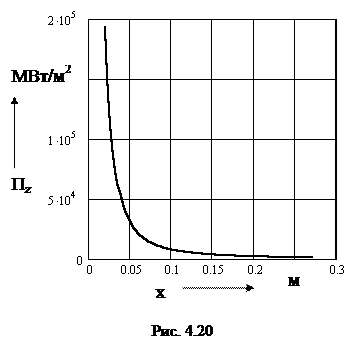Как видно из графика, максимальное значение вектор Пойнтинга принимает на поверхности провода (192800 МВт/м²), а затем он быстро уменьшается и уже на расстоянии, равном 23 см от поверхности, его значение составляет 1113 МВт/м²

Отсюда можно сделать вывод, что вся энергия, которая передается от источника к приемнику, сосредоточена в очень ограниченной области вокруг проводников (график распределения потока мощности около второго провода аналогичен). Внутри проводов вектор Пойнтинга равен нулю, поскольку сопротивление проводов равно нулю, а следовательно и напряженность электрического поля равна нулю.

Пример 3. Провести расчет напряженности электрического и магнитного поля в дальней зоне для антенны, имеющей мачту высотой 100 м, излучающей электромагнитное поле в гектометровом диапазоне при l=400 м мощностью 100 кВт.

Пусть ток вдоль антенны распределен синусоидально и определяется выражением (4.37). В этом случае сопротивление излучения определяется с помощь формулы (4.50) или с помощью графика (рис. 4.16) при l/l=0.25, а затем (для учета влияния земли) делится пополам. Таким образом, сопротивление R_S=36.565 Ом. После этого, с помощью выражения (4.49), находим амплитудное значение тока I₀= 73.96 А.

Поскольку антенна расположена в воздухе, то волновое сопротивление среды Z_В=120p=377 Ом.

Примем расстояние, на котором будем определять напряженность, равным 5000 м, а угол y =0 (рис. 4.11). В этом случае модуль напряженности электрического поля (определяется по формуле (4.43)) будет равен 0.888 В/м, а модуль напряженности магнитного поля Н=Е/ Z_В=0.00235 А/м.