Закон ома для цепей переменного тока

Лабораторная работа №324

Приборы и принадлежности:переменный резистор, катушка индуктивности, конденсатор, амперметр и вольтметр переменного тока.

Введение.Закон Ома и правила Кирхгофа, установленные для постоянного тока, остаются справедливыми для мгновенных значений переменных токов и напряжений в цепях небольшой протяженности и если их изменения происходят не слишком быстро.

Электромагнитные возмущения распространяются по электрической цепи в виде электромагнитной волны со скоростью с . Если за время t=l/c , необходимое для прохождения электрического сигнала от источника в самую удаленную точку цепи (l – размер цепи), сила переменного тока изменяется незначительно, то мгновенные значения тока в любом сечении цепи в данный момент будут практически одинаковы. Токи, удовлетворяющие такому условию, называются квазистационарными. Для периодически изменяющихся токов условие квазистационарности запишется следующим образом:

t = (l/c)<< Т, или l<<l,

где Т – период колебаний переменного тока,

l – длина электромагнитной волны.

Ток промышленной частоты (50 Гц) квазистационарен в цепях протяженностью до 10² км (так как l=6·10⁶ м при Т=1/50 с). Для квазистационарных токов справедливы закон Ома, закон Джоуля-Ленца и др. В условиях данной лабораторной работы мы будем иметь дело с электрическими цепями, протяженность которых существенно меньше приведенной выше.

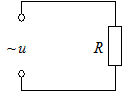1.Пусть цепь переменного тока состоит из источника и резистора R, а емкостным и индуктивным сопротивлениями можно пренебречь в силу их малости. Такого рода нагрузка для источника является активной, т.е. в ней происходит преобразование энергии электрического тока в тепловую или механическую (рис.1). В цепь включен источник переменно-

Рис.1 го тока, на выходе которого напряжение изменяется по закону

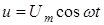, (1)

где u – мгновенное напряжение – напряжение в момент времени t,

U_m – амплитуда напряжения,

w – циклическая частота изменения напряжения.

При выполнении условия квазистационарности ток в любом месте цепи определяется законом Ома

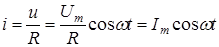, (2)

где I_m – амплитуда тока

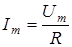. (3)

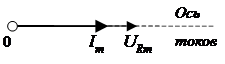Соотношения между токами и напряжениями в различных электрических цепях становятся более наглядными, если их представить в виде векторов на так называемой векторной диаграмме. Как она строится? Выбирают произвольное направление, которое принимают, например, за ось токов (рис.2). Вдоль этого направления откладывают направленный отрезок прямой пропорциональный I_m – вектор тока. Вектор напряжения U_Rm будет направлен туда же, так как согласно соотношению (2) напряжение и ток в случае активной нагрузки изменяются синфазно. Совокупность вектора напряжения и вектора ток образуют векторную диаграмму рассматриваемой электрической цепи. Рис.2

2.Подадим переменное напряжение (1) на катушку индуктивности L с пренебрежимо малым активным сопротивлением (рис.3). По катушке потечет переменный ток i, вследствие чего возникнет ЭДС самоиндукции

.

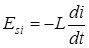В стационарных условиях величина ЭДС самоиндукции уравновешивается приложенным напряжением со стороны источника

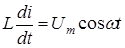, (4)

которое назовем падение напряжения на индуктивности и обозначим u_L

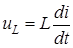. (5)

Перепишем уравнение (4) в виде

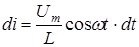(6)

и проинтегрируем его с целью определения тока в цепи

.

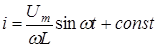Так как в рассматриваемой цепи нет постоянной составляющей тока, то const=0. Таким образом,

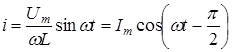, (7)

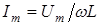где . (8)

Сравнивая полученное выражение (8) с (3), видим, что роль сопротивления в случае индуктивной нагрузки играет величина

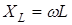, (9)

которую называют индуктивным сопротивлением. Если L взять в генри, w – в с^-1 , то X_L будет выражено в омах. Индуктивное сопротивление растет с увеличением частоты переменного тока w. Постоянному току индуктивность не оказывает сопротивления.

Заменив в формуле (5) U_m на wLI_m, получим следующее выражение для падения напряжения на индуктивности:

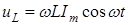. (10)

Из сравнения выражений (7) и (10) видно, что ток, текущий через индуктивность, отстает по фазе от приложенного напряжения u_L на 90°.

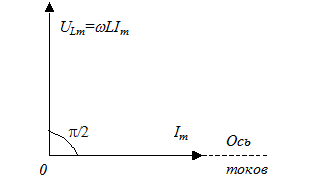
Векторная диаграмма для индуктивной нагрузки приведена на рис.4. Вектор U_Lm проводится под

Рис.4 углом p/2 радиан к вектору Im.

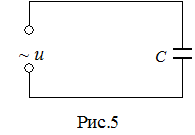3.Пусть на конденсатор емкости С (рис.5) подано переменное напряжение (1), под действием которого конденсатор перезаряжается с частотой n=w/2p, вследствие чего по цепи идет переменный ток. Напряжение на конденсаторе равно приложенному напряжению u

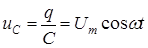. (11)

Отсюда .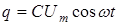

Производная dq/dt дает ток в цепи i

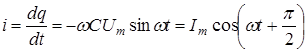
, (12)

где 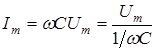. (13)

Сравнение выражений (13) и (3) показывает, что величина 1/wC играет роль сопротивления, его называют емкостным сопротивлением и обозначают X_C.

X_C=1/wC (14)

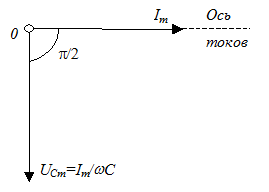Если взять емкость С в фарадах, w – в с^-1, то Х_С получается в омах. Для постоянного тока (w=0) конденсатор представляет бесконечно большое сопротивление. С ростом частоты переменного тока сопротивление конденсатора уменьшается.

При сравнении соотношения (12) с (1) видно, что протекающий через конденсатор ток опережает по фазе приложенное напряжение на 90°. Таким образом, в случае емкостной нагрузки вектор тока на векторной диаграмме повернут относительно вектора напряжения на +p/2 радиан (рис.6). Рис.6

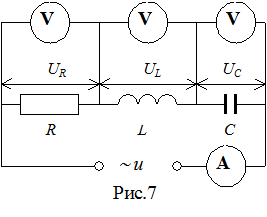4.Рассмотрим электрическую цепь, состоящую из активного сопротивления R, индуктивности L и емкости С, соединенных последовательно между собой и с источником переменного напряжения (рис.7). В цепи установится переменный ток, который вызовет на активном сопротивлении падение напряжения U_R=IR, на индуктивном – U_L=IwL, на емкостном – U_C=I/wC. Все падения напряжения в сумме должны составлять входное напряжение, т.е. напряжение источника U. Здесь U, U_R, U_L, U_C, I – показания соответствующих приборов, т.е. эффективные величины. Эта сумма не может быть арифметической, она может быть только векторной, так как между отдельными слагаемыми существуют фазовые сдвиги. Векторная диаграмма для данной цепи построена с учетом этих сдвигов (рис.8). Вместо амплитудных значений тока и напряжения она построена по эффективным величинам (в отличие от примеров, представленных на рис.2; 4; 6). Это равноценно изменению масштаба диаграммы в 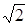раз.

Построение векторной диаграммы производится в следующем порядке.

Из некоторой точки 0 (назовем ее началом) в произвольном направлении (например, горизонтально) проводим прямую, которую назовем осью. В данном случае удобно начать построение с выбора оси токов, поскольку в рассматриваемой цепи ток одинаков во всех ее элементах. Из начала вдоль оси токов проводим направленный отрезок, пропорциональный току I. Это будет вектор тока. В этом же направлении в выбранном масштабе проводим вектор напряжения U_R=IR, так как падение напряжения на активном сопротивлении синфазно току. Из того же начала проводим вектор U_L=ILw под углом +p/2 к вектору тока, так как напряжение на индуктивности опережает ток, и под углом –p/2 проводим вектор U_C=I/Cw, поскольку это напряжение отстает от тока. Складывая все три вектора напряжения, мы получим входное напряжение U.

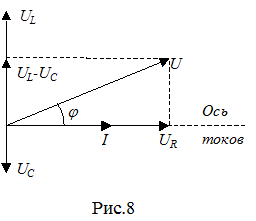Из диаграммы видно, что между приложенным к цепи полным напряжением и током в ней наблюдается сдвиг по фазе. Угол сдвига фаз j определяется следующим образом:

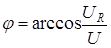, или 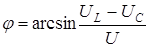. (16)

Из прямоугольного треугольника, гипотенуза которого U , следует, что

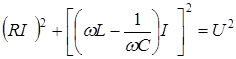, откуда 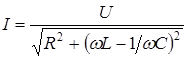. (17)

Величина, равная

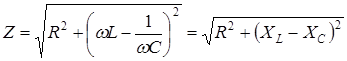, (18)

называется полным сопротивлением цепи.

Итак, если напряжение на входе цепи изменяется по закону

,

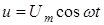то в цепи течет ток

,

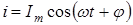где j и I_m определяются формулами (16) и (17). Формула (17) является законом Ома для цепей переменного тока, который можно сформулировать так: переменный ток в участке цепи прямо пропорционален переменному напряжению на этом участке и обратно пропорционален его полному сопротивлению.

В зависимости от величины индуктивного X_L и емкостного X_C сопротивлений ток в цепи может отставать от приложенного напряжения (при X_L>X_C) или опережать его (при X_L<X_C).

Выше был написан закон Ома для переменного тока в случае чисто активной нагрузки (3), индуктивной – (8) и емкостной – (13). Формулы (17) и (18) могут быть применены к цепям, представляющим собой любую комбинацию R,L,C.

Целью данной лабораторной работы является проверка выполнения закона Ома в цепях различной модификации и определение на его основании индуктивности катушки и емкости конденсатора.

Описание установки.Установка состоит из лабораторной панели, на которой помещены переменный резистор, двухсекционная катушка без ферромагнитного сердечника (L₁ – 1200 витков медного провода и L₂ – 2400 витков), две группы конденсаторов: С₁ и С₂ , вольтметр, амперметр и тумблер включения источника тока. В качестве источника используется сеть промышленной частоты (n=50 Гц, w=2pn=314 с^-1) с пониженным до безопасных значений напряжением.

Упражнение 1