Интерференция от клина. Полосы равной толщины 4 страница

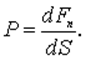По кинетической теории давление газа на стенки сосуда возникает в результате непрерывных ударов о них отдельных молекул. Эти удары молекул о стенки приводят к некоторым смешениям частиц материала стенки и, значит, к ее деформации. Деформированная же стенка действует на газ упругой силой, направленной в каждой точке перпендикулярно к стенке. Сила эта равна по абсолютному значению и противоположна по направлению силе, с которой газ действует на стенку.

Определение температуры в кинетической теории газов. В кинетической теории газов доказывается, что если две подсистемы (из одинаковых или разных молекул) могут обмениваться энергией, то в состоянии равновесия оказываются равными средние кинетические энергии поступательного движения их молекул. Исходя из этого, кинетическая теория газов определяет температуру как величину, пропорциональную средней кинетической энергии поступательного движения молекулы: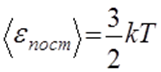

где k — постоянная Больцмана, которая выражается через универсальную газовую постоянную и число Авогадро (см. разд. 2.1): k = R/Na ~1,38•10 -23 Дж/К. Коэффициент пропорциональности выбран так, чтобы уравнение состояния идеального газа.

Внутренняя энергия данной массы идеального газа зависит только от его температуры и не зависит ни от давления, ни от объема.

Билет 14

1.14.

Физический маятник.

Физический маятник - твёрдое тело способное совершать колебания относительно оси, не совпадающей с центром масс.

Используя основной закон динамики вращательного движения, покажите, что при малых углах отклонения он совершает гармонические колебания.

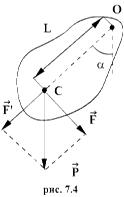
При небольших углах отклонения α (рис. 7.4) физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.

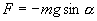
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла α

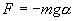
Для вывода закона движения физического маятникА используем основное уравнение динамики вращательного движения

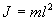. Момент силы: определить в явном виде нельзя. С учетом всех величин, входящих в исходное дифференциальное уравнение колебаний физического маятника имеет вид:

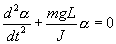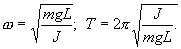Решение этого уравнения

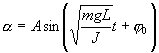
Приведенная длина и период колебаний физического маятника.

Определим длину l математического маятника, при которой период его колебаний равен периоду колебаний физического маятника, т.е. 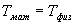или

.
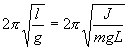Из этого соотношения определяем

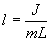
Данная формула определяет приведенную длину физического маятника, т.е. длину такого математического маятника, период колебаний которого равен периоду колебаний данного физического маятника.

5.5 Работа газа, теплоемкость, изменение внутренней энергии, первый закон термодинамики при изопроцессах.

Работой газа называется его неквазистатическое расширение, а также последующее давление на определенную поверхность (как правило данный закон выполним для газа, находящегося в закрытом пространстве, например, поршне) под действием внешних сил. Теплоемкость– свойство материала поглощать определенное количество тепла при нагревании и выделять его при охлаждении. Газ, находящийся в состоянии термодинамического равновесия, можно характеризовать внутренней энергией.

Внутренней энергией называют полную энергию его молекул. В термодинамике она включает в себя суммарную кинетическую энергию теплового движения молекул и потенциальную энергию их взаимодействия. Закон Генри — закон, по которому при постоянной температуре растворимость газа в данной жидкости прямо пропорциональна давлению этого газа над раствором. Закон пригоден лишь для идеальных растворов и невысоких давлений. Собственно, закон Генри констатирует достаточно простой факт: чем выше давление газа над поверхностью жидкости, тем труднее растворенному в ней газу высвободиться. И это совершенно логично с точки зрения молекулярно-кинетической теории, поскольку молекуле газа, чтобы вырваться на свободу с поверхности жидкости, нужно преодолеть энергию соударений с молекулами газа над поверхностью, а чем выше давление и, как следствие, число молекул в приграничной области, тем сложнее растворенной молекуле преодолеть этот барьер.

Билет 15

3.11

Дифракционная решетка. Схема и преимущества осуществления дифракции света на решетке.

Главные максимумы, условие их возникновения.

Дифракционный спектр. Дифракционная картина при освещении решетки белым светом.

1)Дифракционная решетка представляет собой совокупность большого числа равноотстоящих щелей, нанесенных на стеклянной или металлической поверхности.

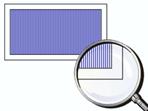
Период решетки d - это сумма ширины щели b и расстояния между щелями a.

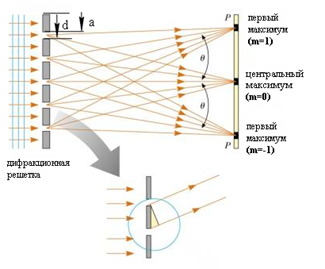
2)

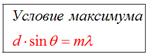
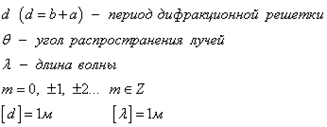
3) Дифракционный спектр - получается при прохождении света сквозь большое число малых отверстий и щелей(Дифракционную решётку)

2.2.

Электростатическое поле.

Электростатическое поле — поле, созданное неподвижными в пространстве и неизменными во времени электрическими зарядами (при отсутствии электрических токов). Электрическое поле представляет собой особый вид материи, связанный с электрическими зарядами и передающий действия зарядов друг на друга.

Основные характеристики электростатического поля:

· напряженность

· потенциал

Напряженность и электрическое смещение электростатического поля.

Напряженность электростатического поля - это силовая характеристика электростатического поля, численно равная силе, действующей на единичный положительный заряд.

Напряженность электростатического поля - векторная величина: E = F/Qпробный

Единица напряженности - вольт на метр (В/м)

Электростатическое поле представляется графически силовыми линиями или линиями напряженности .

Электри́ческая инду́кция (электри́ческое смеще́ние) — векторная величина, равная сумме вектора напряжённости электрического поля и вектора поляризации(Смещение электрических зарядов вещества под действием электрического поля)

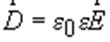Единицей электрического смещения является кулон на метр квадратный (Кл/м²).

, где e0 – электрическая постоянная; e – относительная диэлектрическая проницаемость среды; 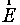– вектор напряженности электрического поля.

Направление вектора электрического смещения 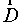совпадает с направлением вектора напряженности 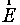. Согласно определению вектора электрического смещения 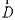и выражения можно записать

.

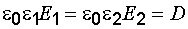Напряженность поля точечного заряда.

Напряженность электростатического поля (точечного заряда): 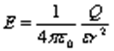где r - расстояние от заряда Q, создающего поле, до точки поля, в которой определяется напряженность

Примеры формул напряженности поля заряженных тел.

1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.

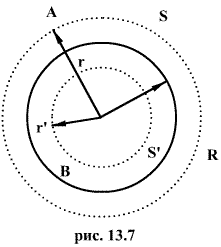Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность 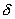заряда в любой точке сферы будет одинакова.

Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R. Поток вектора напряженности через поверхность S будет равен

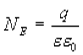
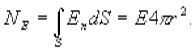
По теореме Гаусса

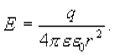
Следовательно

Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.

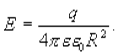Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать

Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. 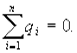Следовательно, по теореме Гаусса, 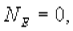и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю.

Ядерная модель атома.

Результаты квантово-механического рассмотрения поведения электрона в водородоподобном атоме.

Излучение и поглощение энергии атомами и молекулами.

Большие успехи в исследовании строения атомов были достигнуты в опытах английского ученого Эрнеста Резерфорда по рассеянию α-частиц при прохождении через тонкие слои вещества. В этих опытах узкий пучок α-частиц, испускаемых радиоактивным веществом, направлялся на тонкую золотую фольгу. За фольгой помещался экран, способный светиться под ударами быстрых частиц. Было обнаружено, что большинство α частиц отклоняется от прямолинейного распространения после прохождения фольги, т. е. рассеивается, а некоторые α-частицы вообще отбрасываются назад. Рассеяние α-частиц Резерфорд объяснил тем, что положительный заряд не распределен равномерно в шаре радиусом 10^(-10)м, как предполагали ранее, а сосредоточен в центральной части атома — атомном ядре. При прохождении около ядра α-частица, имеющая положительный заряд, отталкивается от него, а при попадании в ядро — отбрасывается в противоположном направлении. Так ведут себя частицы, имеющие одинаковый заряд, следовательно, существует центральная положительно заряженная часть атома, в которой сосредоточена значительная масса атома. Расчеты показали, что для объяснения опытов нужно принять радиус атомного ядра равным примерно 10^(-15) м.

Резерфорд предположил, что атом устроен подобно планетарной системе. Суть модели строения атома по Резерфорду заключается в следующем: в центре атома находится положительно заряженное ядро, в котором сосредоточена вся масса, вокруг ядра по круговым орбитам на больших расстояниях вращаются электроны (как планеты вокруг Солнца). Заряд ядра совпадает с номером химического элемента в таблице Менделеева.

Атом водорода состоит из положительно заряженных протона Р и одного электрона е.

n - главное квантовое число; n=1,2,3…; ℓ- орбитальное квантовое число; l=1,2,3…(n-1); m- магнитное квантовое число m=-1,…,0,…,1; J-спиновое квантовое число J=+1/2;-1/2

В состоянии покоя е находится на нижнем уровне. Поглощая W, е переходит на более высокий уровень (переходит в возбужденное состояние).

Время жизни е в возбужд. состоянии - 10-8с, после чего е переходит на уровень ниже.

Возвращение на предыдущий уровень сопровождается излучением фотонов с определенным количеством энергии.

Основные серии переходов: 1) Лаймана (n=1), 2) Бальмера (n=2), 3) Пашена (n=3).

Билет 16

1.12.

Кинематика колебательного движения: смещение, амплитуда, фаза, циклическая частота.

Колебательные движения –– это движения, повторяющиеся во времени. Простейшей периодической функцией является гармоническая функция cos или sin.

Характеристика колебаний

Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.

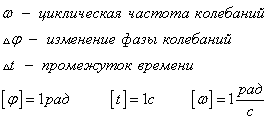Циклическая частота характеризует скорость изменения фазы колебаний.

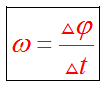
Начальное состояние колебательной системы характеризует начальная фаза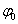

Амплитуда колебаний A - это наибольшее смещение из положения равновесия

Период T - это промежуток времени, в течение которого точка выполняет одно полное колебание.

Частота колебаний - это число полных колебаний в единицу времени t.

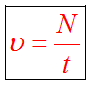
Частота, циклическая частота и период колебаний соотносятся как

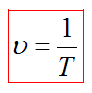
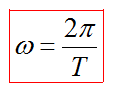
Уравнение гармонических колебаний.

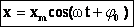
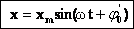
Скорость и ускорение точки, совершающей гармонические колебания.

Согласно определению скорости, скорость – это производная от координаты по времени

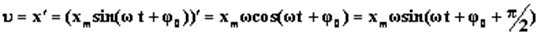
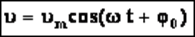
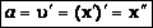Согласно определению ускорения, ускорение – это производная от скорости по времени:

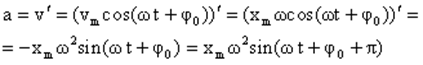- вторая производная от координаты по времени.

Тогда:

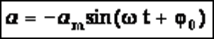
2.5.

Электрический ток.

Электри́ческий ток — направленное (упорядоченное) движение заряженных частиц

Условия возникновения и существования электрического тока.

1. наличие свободных носителей зарядов,

2. наличие разности потенциалов. это условия возникновения тока,

3. замкнутая цепь,

4. источник сторонних сил, который поддерживает разность потенциалов.

Сторонние силы.

Сторонние силы - силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока. Сторонними считаются все силы отличные от кулоновских сил.

Э.д.с. Напряжение.

Электродвижущая сила (ЭДС) — физическая величина, характеризующая работу сторонних (непотенциальных) сил в источниках постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работе этих сил по перемещению единичного положительного заряда вдоль контура.

ЭДС можно выразить через напряжённость электрического поля сторонних сил

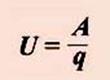Напряжение ( U ) равно отношению работы электрического поля по перемещению заряда
к величине перемещаемого заряда на участке цепи.


Единица измерения напряжения в системе СИ:

[ U ] = 1 B

Сила тока.

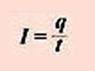Сила тока ( I )- скалярная величина, равная отношению заряда q , прошедшего через поперечное сечение проводника, к промежутку времени t , в течение которого шел ток. Сила тока показывает, какой заряд проходит через поперечное сечение проводника за единицу времени.

Плотность тока.

Плотность тока j — вектор, модуль которого равен отношению силы тока, протекающего через некоторую площадку, перпендикулярно направлению тока, к величине этой площадки.

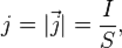
В СИ единицей плотности тока является ампер на квадратный метр (А/м2).

Выражение плотности тока через характеристики переносчиков заряда.

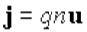
Плотность тока j для отрицательных носителей направлена противоположно скорости u. Направление вектора плотности тока называют направлением электрического тока. Таким образом, для положительных зарядов направление тока совпадает с направлением движения носителей, для отрицательных – противоположно ему.

В том случае, когда существует разброс носителей тока по скоростям, под u следует понимать среднюю скорость направленного движения носителей тока. Если в переносе заряда участвуют носители разных типов (электроны и дырки в полупроводнике, ионы разного типа в электролите), то плотность тока определяется формулой

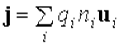, где суммирование ведется по разным типам носителей.

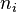— концентрация частиц каждого типа,

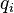— заряд частицы данного типа,

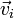— вектор средней скорости частиц этого типа.

3.10

Дифракция Фраунгофера (дифракция в параллельных лучах), ее отличие от дифракции Френеля. Способы осуществления дифракции Фраунгофера.

Дифракция Фраунгофера от одной щели. Условия максимумов и минимумов дифракции. Распределение интенсивности света по экрану.

1)Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка 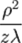, что сильно упрощает теоретическое рассмотрение явления. Здесь — расстояние от отверстия или преграды до плоскости наблюдения, 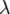— длина волны излучения, а — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Дифракционные явления Фраунгофера имеют большое практическое значение, лежат в основе принципа действия многих спектральных приборов, в частности, дифракционных решёток. В последнем случае для наблюдения светового поля «в бесконечности» используются линзы или вогнутые дифракционные решетки (соответственно, экран ставится в фокальной плоскости).

Дифракция Френеля: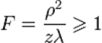

Дифракция Фраунгофера: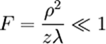