Проводимость полупроводников и металлов.

Величина электрического тока I через образец, например в виде параллелепипеда, определяется в зависимости от напряжения U и сопротивления образца R:

I = U/R = US/rl = gUS/l = gSE (1)

Где I – ток; l - длина образца; S - площадь; R - сопротивление; r- удельное объемное сопротивление; g - проводимость материала.

Из этого соотношения видно, что проводимость связана с величиной напряженности электрического поля Е = U/l и плотностью тока j = I/S:

g = j/E или j = gE (2)

Величина g полупроводников и металлов существенно зависит от температуры кристаллов.

Электрический ток в твердом теле обусловлен передвижением свободных заряженных частиц. В металлах электрический ток возникает вследствие перемещения свободных электронов, в полупроводниках – свободных электронов и дырок.

Величина g зависит от концентрации n и р и подвижности m_n и m_р. Величина подвижности определяется как отношение дрейфовой скорости v_др к напряженности поля

m = v_др/Е; [m] = м²/В×с (3)

Допустим, что в образце имеется определенная концентрация носителей – электронов n. Приложение к образцу напряжения U Создает напряженность Е = U/l, и вцепи протекает ток I_n, обусловленный передвижением электронов с дрейфовой скоростью v_n.

Анализ показывает, что через поперечное сечение образца протекает ток, равный

I_n = Q_n/t = env_ntS/t = env_nS = enm_nES (4)

Где Q_n – заряд, прошедший через поперечное сечение S за время t ; е – заряд электрона.

С учетом соотношения (2) имеем

g_n = enm_n (5)

В общем случае при наличии носителей n- и р-типа

g = g_n + g_p = enm_n + epm_p (6)

Из соотношений (2) и (6) видно, что плотность тока j в цепи определяется величинами проводимости g и напряженности электрического поля, при фиксированной напряженности электрического поля (постоянном напряжении на образце) плотность тока определяется только величиной проводимости. Величина g в свою очередь зависит от значений n,p и m_n , m_р, определяемых температурой, типом материала и примесей.

Зависимость концентрации носителей заряда

В полупроводниках и металлах от температуры.

Металлы.

При образовании кристаллической решетки металлов каждый атом решетки отдает один валентный электрон в «электронный газ» металла. Вследствие этого при любой температуре число электронов, способных участвовать в процессе проводимости, остается практически неизменным и равно плотности узлов решетки: n @ 10²⁸ м^-3 .

Зонная диаграмма металла приведена на рис.5.а. В металле при любой температуре электроны находятся в зоне проводимости, физически это означает, что они свободны и могут передвигаться по кристаллу. При Т = 0_оК все электроны имеют нижние значения энергии ( скорость носителей ограничена при этой температуре значением v_ф , энергия ограничена значением Е_ф = mv²_ф/2, ( Е_ф – энергия уровня Ферми). При увеличении температуры ( Т > 0оК)ьбэлектроны могут увеличивать свою скорость (энергию), поэтому значения энергии некоторых носителей будут больше значения Е_ф, на зонной диаграмме увеличение энергии электрона изображается переходом 1 ( рис. 4.а).

Полупроводники.

Количество носителей заряда в полупроводниках существенно зависит от температуры и типа материала. Зонные диаграммы полупроводников различных типов представлены на рис. 4.б-г.

При температуре 0^оК свободные носители отсутствуют; в собственном полупроводнике все носители связаны с собственными атомами материала ( на языке зонной диаграммы это означает, что носители находятся в валентной зоне). Собственный полупроводник имеет уровень Ферми Е_ф посередине запрещенной зоны.

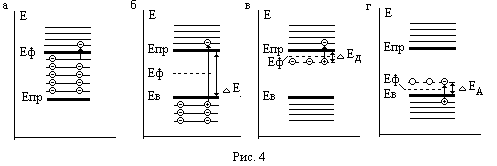В донорном полупроводнике при Т=0 все свободные носители также отсутствуют, они связаны с собственными атомами материала ( находятся в валентной зоне) и с атомами примеси ( находятся на уровне Е_д).

Уровень энергии Е_фn для примесного донорного полупроводнтка при низких температурах находится вблизи дна зоны проводимости (рис.4.в).

В акцепторном полупроводнике при Т=0 все свободные носители также отсутствуют; электроны связаны с собственными атомами материала ( находятся в валентной зоне), атомы примеси (акцепторы) не ионизованы. При увеличении температуры собственные атомы начинают ионизоваться, электрон захватывается акцептором ( электрон находится на уровне акцептора Е_а) и появляется дырка (в валентной зоне). Уровень энергии Е_фр для примесного акцепторного полупроводника находится вблизи потолка валентной зоны (рис. 4.г)

В собственных полупроводниках носители заряда ( электроны и дырки) появляются вследствие ионизации собственных атомов. Концентрация собственных носителей увеличиваетс с повышением температуры согласно выражению:

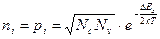(7)

где N_c, N_v – плотности состояний (уровней) в зоне проводимости и валентной зоне; Т – температура кристалла,К; DЕ_з – ширина запрещенной зоны; к – постоянная Больцмана.

Логарифмируя выражение (7), получаем

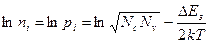(8)

Если пренебречь зависимостью N_c, N_v от температуры, то n(T) описывается прямой линией в координатах ln n от (1/T, К) (рис 5.а)

В примесных полупроводниках образование носителей обусловлено генерацией как из собственных атомов, так и с примесных центров.

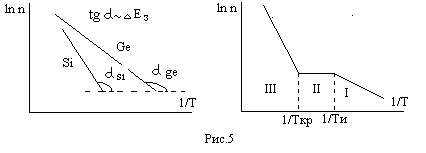Поскольку энергия ионизации , например донорной примеси DЕ_д гораздо меньше ширины запрещенной зоны DЕ_з , то при увеличении температуры от 0^оК в первую очередь начнут ионизоваться примесные центры – доноры.

В диапазоне температур 0 – 150^оК зависимость n(T) представляется в виде

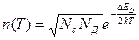(9)

где Ед – энергия ионизации доноров; Nд – концентрация доноров.

В координатах ln n(T) = f(1/T) зависимость n(T) представляется отрезком прямой линии ( рис 5.б, участок 1).

Увеличение температуры выше температуры ионизации примесей Т_и приводит к полной ионизации доноров, поэтому дальнейшее возрастание температуры не влияет на ионизацию. Это приводит к тому, что в диапазоне Т_кр< Т < Т_и концентрацция носителей остается постоянной ( Т_кр – температура, при которой концентрация генерируемых собственных носителей становится сравнимой с концентрацией доноров).

Таким образом в области температур Т=300 – 400 ^оК доноры ионизованы полностью, концентрация электронов примесного происхождения намного превышает концентрацию электронов собственного происхождения даже при ничтожном количестве примеси. Например, кремний, легированный примесью в количестве 0,001%, считается химически чистым. В то же время, это соответствует концентрации примесей 10²³ м^-3 (концентрация атомов кремния 10²⁸ м^-3).

Поскольку при Т=300 – 400 ^оК все атомы примеси ионизованы, концентрация свободных электронов примесного происхождения будет равна 10²³ м^-3, что намного больше концентрации свободных электронов и дырок собственного происхождения (при 300^оК n_i = 10¹⁶ м^-3). Следовательно, введение ничтожного количества примеси повысило концентрацию электронов по сравнению с концентрацией электронов собственного происхождения на семь порядков. Поэтому при Т=300 – 400 ^оК концентрацией электронов собственного происхождения можно пренебречь и считать, что в донорном полупроводнике концентрация основных носителей определяется только электронами примесного происхождения, т.е. n_n = N_д.

При температурах Т > Т_кр генерация носителей собственного происхождения создает количество носителей (электронов и дырок), превышающее количество электронов примесного происхождения, в этом диапазоне зависимость n(T) описывается соотношением (7).

Методические указания.

Статическая вольт-амперная характеристика кристалла снимается путем исследования зависимости тока в кристалле от напряжения I(U_n ). Сопротивление кристалла определяется графически по зависимости I(U_n ):

.

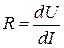Значение удельного сопротивления r и электропроводности определяется с учетом соотношения (1) и (2 ).

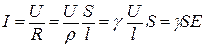(1),

где I – ток, l – длина образца, S – площадь, R – сопротивление, r - удельное объемное сопротивление, g- проводимость материала. Параметры кристалла (длина и площадь сечения) указаны на стенде.

Из соотношения (1) имеем, что проводимость связана с величиной напряженности электрического поля 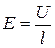и плотностью тока :

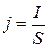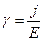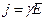или (2).

Величина s полупроводников и металлов существенно зависит от температуры кристаллов.

Нагрев кристалла производится косвенным образом с помощью нагревателя. Температура кристалла фиксируется в процессе нагрева с помощью термопары.

В процессе нагрева образца снимается зависимость тока от температуры, после чего рассчитывается и строится зависимость .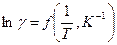

С учетом соотношения 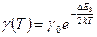(3),

где DE₃ – энергия активации собственных носителей (ширина запрещенной зоны), s¢₀ (Т) – параметр, мало зависящий от температуры, имеем

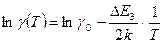(4).

Таким образом, в координатах ln g(1/T) зависимость проводимости от температуры представляется прямой линией с наклоном, равным

,

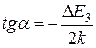Где DE₃ - ширина запрещенной зоны полупроводника, k – постоянная Больцмана (k = 8,625 × 10^-5 эВ/K=1,38×10^-23 Дж/K).

На графике по оси абсцисс откладываются значения 1/T (Т⁰ К) по оси ординат – значение натурального логарифма проводимости материала (g).

С учетом температурной зависимости электропроводности полупроводников, описываемой соотношением (3), сопротивление полупроводникового резистора изменяется с температурой

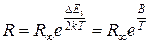(5),

где 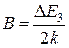- коэффициент температурной чувствительности, зависящий от типа примеси, ширины запрещенной зоны, энергии активации примеси и т.п.; R_¥ - постоянная, зависящая от материала и размеров полупроводника, Т – температура в градусах Кельвина.

На практике широко используются сопротивления, у которых ширина запрещенной зоны весьма мала ( 0,1 – 0,3 эВ), вследствие чего при возрастании температуры значение сопротивления резко уменьшается (термисторы). Сопротивление термисторов имеет значение от нескольких Ом до нескольких сотен килоом.

Коэффициент температурной чувствительности В ( 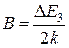) имеет значение от 700 до 15000 К и практически одинаков для данного термистора в рабочем диапазоне температур.

Температурный коэффициент сопротивления термистора показывает относительное изменение сопротивления термистора при изменении тепрературы на 1 Кельвин

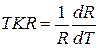(6).

Температурный коэффициент зависит от температуры, поэтому его необходимо записывать с индексом, указывающим температуру, при которой имеет место данное значение. С учетом (5) имеем

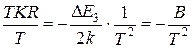(7).

Значение TKR при комнатной температуре различных термисторов находятся в пределах –(0,8 – 6,0)×10^-2 К^-1 . Обратим внимание на то, что термисторы имеют отрицательный температурный коэффициент сопротивления.

В качестве рабочего элемента термистора выбираются полупроводники на основе окислов металлов, например, цинка, титана.

Работа полупроводниковых приборов, позисторов, основана на возрастании сопротивления материала при увеличении температуры. Это обусловлено уменьшением подвижности носителей заряда в области высоких температур, вследствие чего проводимость полупроводника начинает уменьшаться. В итоге, сопротивление позистора возрастает при увеличении температуры кристалла. Отметим, что позистор, в частности, при большом увеличении температуры полупроводник переходит в область собственной проводимости, и его сопротивление начнет уменьшаться.

Рабочим элементом позисторов является специальная керамика на основе соединений титана бария.

Термисторы и позисторы используются в электронных схемах для регистрации температуры окружающей среды, оценки потоков различных излучений, например, оптического излучения лазеров, ядерного, рентгеновского и т.п., в схемах сигнализации и т.д.

Измерения и обработка результатов

1. Произвести анализ схемы (рис.1).

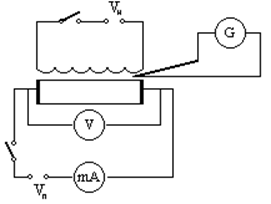
Рис.1

2. По разрешению преподавателя включить питание схемы: подать напряжение на полупроводник.

I. Снятие вольтамперной характеристики полупроводника при комнатной температуре Т₀ (значение Т₀ определяется в лаборатории) .

1. Увеличивая потенциометром напряжение от 0 до 60 В через каждые 10 В снимите зависимость силы тока, протекающего через проводник, от напряжения. Данные занесите в таблицу 1.

Таблица 1.

№ пп	U, В	I, мА	R, Ом	R ± DR	r, Ом м	s, См/м
1.
2.
….
10.

2. По полученным данным постройте график зависимости I = f(U) при комнатной температуре ( график прямой строить по методу наименьших квадратов) .

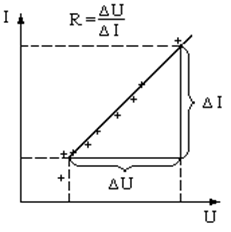
Рис.2

3. Вычислите сопротивление полупроводника для каждого измерения по формуле .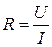

6. Вычислите среднее значение удельного сопротивления r и среднее значение удельной проводимости g с учетом его параметров (кристалл имеет форму цилиндра: длина l = 10 мм, диаметр d = 1мм ). Значение удельного сопротивления r и электропроводность g определяются по соотношениям:

,

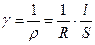где l – длина кристалла, S – площадь сечения кристалла.

Результаты занесите в таблицу 1.

II. Исследование температурной зависимости электропроводности полупроводника.

1. Установить по указанию преподавателя напряжение на кристалле. Определить значение тока при комнатной температуре.

2. Включить нагрев полупроводника. Нагрев кристалла производится с помощью нагревателя включаемого тумблером «Вкл. нагревателя». Температура кристалла регистрируется в процессе нагрева. В процессе нагрева изменится сопротивление и, следовательно, ток через кристалл. Зафиксировать значение тока образца при разных температурах в диапазоне до 90⁰ С. Данные занесите в таблицу 2.

Таблица 2.

U = … В
№ пп	Т0, С	Т, К	1/Т, К-1	I(Т), мА	R, Ом	s, См/м	lns
1.
2.
3.	…
4.

3. Отключите установку от сети.

4. В процессе нагрева образца снимается зависимость тока от напряжения и по полученным данным находится значение

.

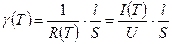5. Рассчитать зависимость lng = f(1/T) и построить график для исследуемого образца.

,

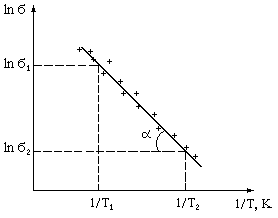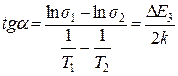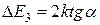В координатах lng (1/Т) зависимость проводимости от температуры представляется прямой линией с наклоном равным 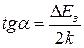, где DЕ₃ – ширина запрещенной зоны, k = 1,38×10²³ Дж/К=8,625×10^-5 эВ/K ‑ постоянная Больцмана; Т – термодинамическая температура;

5. Рассчитать ширину запрещенной зоны DЕ₃ (эВ) по формуле

.

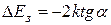Вопросы для защиты работы.

1. Нарисуйте зонную диаграмму собственного и примесного (акцепторного и донорного полупроводника.

2. В каких полупроводниках (собственных или примесных) при комнатной температуре больше свободных носителей зарядов?

3. Может ли энергия свободного носителя иметь значение Е_в < Е < Е_пр?

4. Как изменяется концентрация основных носителей заряда в примесном полупроводнике при возрастании концентрации примесей?

5. Как изменяется концентрация неосновных носителей заряда в примесном полупроводнике при возрастании концентрации примесей?

6. Германий и кремний имеют одинаковое количество примесных центров. В каком полупроводнике концентрация неосновных носителей при комнатной температуре больше?

7. Нарисуйте зависимость ln n(1/T) для собственных и примесных полупроводников.

8. Может ли проводимость полупроводников уменьшаться с ростом температуры?

9. Как определить ширину запрещенной зоны полупроводников?

ЛАБОРАТОРНАЯ РАБОТА 16

ИЗУЧЕНИЕ ФОТОРЕЗИСТОРОВ

Ц е л ь р а б о т ы: Исследовать характеристики сернисто-кадмиевого фотосопротивления

ФС-К1 ,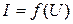

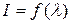
О б о р у д о в а н и е : Фоторезистор, источник монохроматического света, микроамперметр, вольтметр, амперметр, реостаты, источники питания.

Теоретические сведения

Фотопроводимость – это возникновение проводимости вещества под действием света. Увеличение электропроводимости при освещении, как показывает опыт, связано с увеличением концентрации носителей тока.

Существует три пути увеличения концентрации под действием света:

1. Кванты света вырывают электрон из заполненной зоны и забрасывают его в зону проводимости (Рис.1), одновременно возрастает число дырок и электронов. Энергия фотона при этом должна быть несколько больше ширины запрещенной зоны полупроводника:

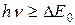(1).

2. Электроны под действием света вырываются из заполненной (валентной) зоны и забрасываются на свободные примесные уровни, при этом возрастает дырочная проводимость (Рис.2), энергия кванта немного больше больше энергии активации акцепторов:

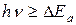(2).

3. Электроны под действием света забрасываются с примесных уровней в свободную зону и увеличивается электронная проводимость (рис.3). Энергия квантов света при этом немного больше энергии донорных примесей:

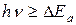
Процесс внутреннего освобождения электронов под действием света является внутренним фотоэффектом.

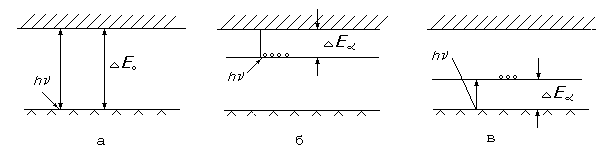
Рис.1

На рис.1 представлена схема образования фотоносителей в полупроводнике: а – собственном, б – донорном, в – акцепторном.

Минимальную частоту n₀ (или максимальную длину волны l₀) при котором свт может еще образовывать фотоносители, т.е. является фотоэлектрически активным, называют красной границей фотопроводимости. Из формул (1 – 2) можно определить красную границу фотопроводимости:

Для собственных полупроводников ;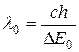

Для примесных полупроводников ,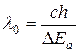

Где с – скорость распространения света в вакууме, h – постоянная Планка.

Для собственных полупроводников, ширина запрещенной зоны которых 2¸3 эВ, красная граница фотороводимости приходится на видимую часть спектра. Многие примесные полупроводники имеют энергию активации примесей порядка десятых долей электрон-вольта. Красная граница фотопроводимости для них лежит в инфракрасной области спектра.

В собственном полупроводнике фотопроводимость связана с перебросами электрона из валентной зоны в зону проводимости. Красная граница определяется наименьшей энергией, необходимой для такого переброса, т.е., на первый взгляд, должна определяться соотношением:

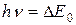(3).

Однако это не вполне точно. Дело в том, что поглощении света должен соблюдаться не только закон сохранения энергии, но и закон сохранения импульса. Электрон “проглотивший” фотон, получает не только энергию, но и импульс:

.

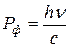В общем случае, когда электрон вырывается светом с произвольного уровня валентной зоны, на котором он имел скорость V₁ , выбрасывается в зону проводимости на уровень, где его скорость станет V₂ , закон сохранения энергии и импульса имеет вид:

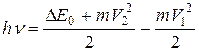(4)

.

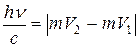Если учесть, что импульс фотона относительно мал (так как скорость света очень велика), то 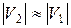и формулы (3) и (4) дают близкие значения. Поэтому для приближенной оценки ширины запрещенной зоны полупроводника можно пользоваться формулой (3).

При 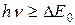коэффициент поглощения очень велик; практически весь свет поглощается в очень тонком поверхностном слое полупроводника. При этом концентрация фотоэлектронов оказывается очень большой и увеличивает вероятность рекомбинации (т.е. их обратного перехода в валентную зону с уменьшением времени жизни носителей). Кроме того, в поверхностном слое всегда имеется большое количество дефектов и примесей, затрудняющих дрейф свободных электронов.

В силу этих причин свет с частотой 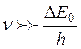поглощается поверхностным слоем и не вызывает заметного фотоэффекта.

Законы сохранения энергии и импульса в случае примесного полупроводника имеют более сложную форму и в данной работе не рассматриваются.

Наряду с ионизацией атома основной решетки возможно и другое возбуждкенное состояние основного атома, при котором электрон не отрывается от него, а лишь переходит на один из незаполненных уровней. Иначе говоря, электрон не разрывает связи с дыркой, а образует с ней единую систему. Такая система называется экситонной.Уровни энергии экситонов располагаются у дна зоны проводимости (рис.2).

Рис.2

Движение экситона можно представить как совместное перемещение электрона и дырки. Грубо это выглядит так: экситон на данном этапе “захлопывается”, т.е. электрон переходит в нормальное состояние. Выделившийся при этом экситон передается соседнему атому. Так как экситон является электрически нейтральной системой, то их возникновение в полупроводнике не приводит к увеличению проводимости. В настоящее время предполагается, что экситоны возникают при фотоэлектрически активном поглощении света. Возникнув, они некоторое время блуждают по объему полупроводника. При столкновении с примесными атомами или другими дефектами решетки экситоны или рекомбинируют или “разрываются”. В первом случае возбужденный атом переходит в нормальное состояние, а энергия излучается в виде квантов света. Во втором случае образуется пара носителей – электрон-“дырка”, которая вносит вклад в фотопроводимость полупроводника.

На фотопроводимость полупроводника существенное влияние оказывает температура. С понижением температуры понижается число носителей тока. Это приводит, во-первых, к увеличению относительной доли фотопроводимости в общей проводимости полупроводника, во-вторых, к увеличению абсолютной величины фотопроводимости, т.к. с уменьшением концентрации носителей тока уменьшается вероятность рекомбинации фотоносителей.

Изменение температуры называет изменение красной границы фотопроводимости, т.к. изменяется величина ширины запрещенной зоны.

Полупроводниковые фоторезисторы широко применяются на практике. Они являются световыми реле. Фоторезисторы имеют одинаковую проводимость в обоих направлениях.

В отличие от фотоэлементов в фоторезисторах под действием света фото э.д.с. не возникает. Фоторезисторы имеют различную чувствительность к разным длинам волн. Например, ФС-А1 наиболее чувствительны к инфракрасной области спектра (l_max =2,2 мкм), ФСК – к видимой области спектра (l_max =0,38 – 0,78 мкм), а ФС-Б – на границе видимой и инфракрасной областей (l_max = 0,7 мкм).

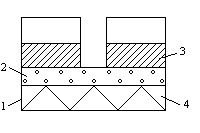
Рис.3

Конструктивно фоторезисторы представляют собой обычные омические резисторы, состоящие из пластмассового корпуса 1, полупроводникового слоя 2, заключенного между токопроводящими электродами 3 и изолирующей прокладки 4 (рис.3).

Измерение и обработка результатов

Схема установки

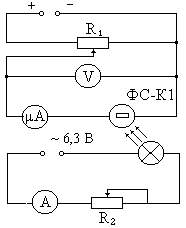
1. Установите ток накала нити лампы в пределах 3 -3,5 А.

2. Снимите вольтамперную характеристику фоторезистора 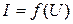меняя напряжение с помощью потенциометра через каждые 5 В. При этом 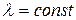(задается преподавателем). Данные измерений занесите в таблицу 1.

Таблица 1.

№ пп	l=const	U, В	I, мкА
1.
2.
3.
4.
5.

3. Освещая фоторезистор светом различной длины волны, снимите зависимость 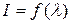, при этом 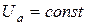(U_а - задается преподавателем). Отсчеты снимайте через 25 нм в интервале от 300 до 900 нм. Данные измерений занесите в таблицу 2.

Таблица 2.

№ пп	Ua=const	λ, нм	I, мкА
1.
2.
3.
4.
5.
6.
7.
8.

Полученные результаты изобразите графически.

4. По графику определите 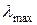- длину волны, к которой фоторезистор наиболее чувствителен.

5. По формуле 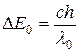оцените ширину запрещенной зоны сернистого кадмия.

Контрольные вопросы

1. Чем объясняется увеличение проводимости полупроводников при их освещении?

2. Почему при 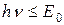не выполняется заметный фотоэффект?

3. Что такое экситоны?

4. Как изменяется фотопроводимость полупроводников с изменением температуры?