Лабораторная работа № 5 эффект Комптона

Введение

Недостаточность волновой теории рассеяния рентгеновских лучей, обнаруживающаяся при изучении интенсивности рассеяния очень коротких длин волн, особенно резко сказывается, если обратиться к рассмотрению частоты рассеянных лучей. Согласно волновой теории механизм рассеяния состоит «в раскачивании» электронов электромагнитным полем падающей волны. Естественно ожидать поэтому, что частота рассеянного излучения должна совпадать с частотой падающего излучения.

Между тем уже старые наблюдения показывали, что при рассеянии рентгеновских и особенно g- лучей длина волны изменяется, а именно, в составе рассеянного излучения появляются более длинные волны, обладающие меньшей проницающей способностью. Так как до открытия спектроскопии рентгеновских лучей для определения длины волны приходилось пользоваться грубыми методами, основанными на различии абсорбции лучей разных длин волн, то в деталях явления разобраться было трудно, и его обычно приписывали влиянию вторичных факторов.

В 1922—1923 гг. А. Комптон, воспользовавшись рентгеновским спектрографом, тщательно изучил это явление и показал, что оно отнюдь не может быть сведено к влиянию побочных факторов, но непосредственно связано с самим механизмом рассеяния.

Рис. 1. Схема опыта Комптона.

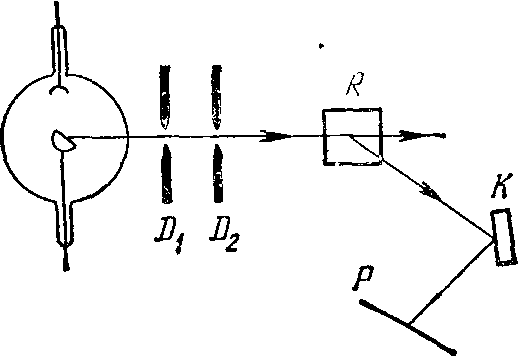Схема опыта Комптона приведена на рис. 1.

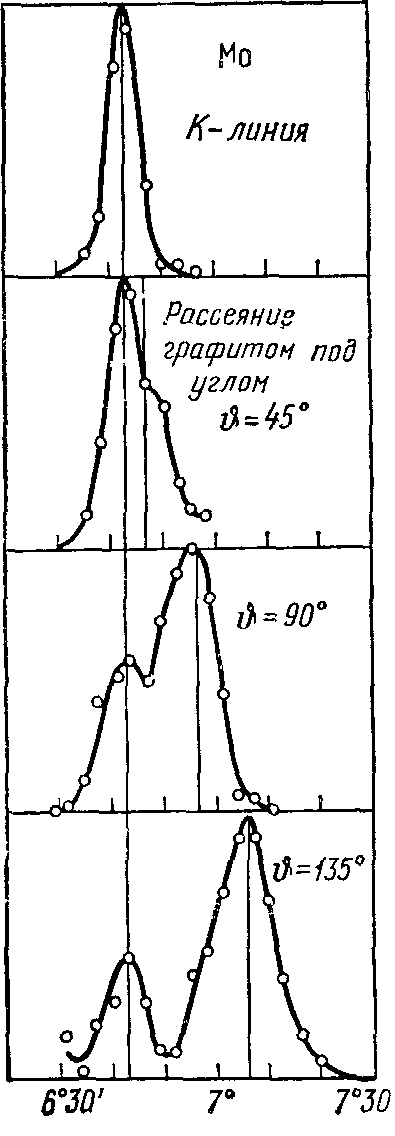
Рис. 2. Эффект Комптона на графите.

Источником рентгеновского излучения служила рентгеновская трубка с молибденовым антикатодом. Узкий пучок монохроматического рентгеновского излучения выделялся диафрагмами D₁ и D₂ и рассеивался на исследуемом теле R. Для исследования спектрального состав рассеянного излучения оно после прохождения ряда диафрагм попадало на монокристалл графита K рентгеновского спектрографа, а затем на фотопластинку P.

На рис. 2 представлены результаты измерений при различных углах рассеяния для K-линии молибдена (l = 0,0712605 нм). Сверху показана форма линии исходного излучения (т. е. угловое распределение интенсивности в линии). Ниже сделано то же самое для рассеянного излучения при различных значениях угла рассеяния. Ясно видно, что первоначально одиночная линия в результате рассеяния становится двойной. Можно сразу установить следующие особенности явления:

1. В рассеянном излучении присутствуют как первоначальная длина волны возбуждающего излучения, так и длина волны, смещенная в сторону длинных волн.

2. Величина смещения зависит от угла рассеяния, а именно, она возрастает при увеличении этого угла.

3. При увеличении угла рассеяния интенсивность несмещенной линии падает, а интенсивность смещенной линии возрастает.

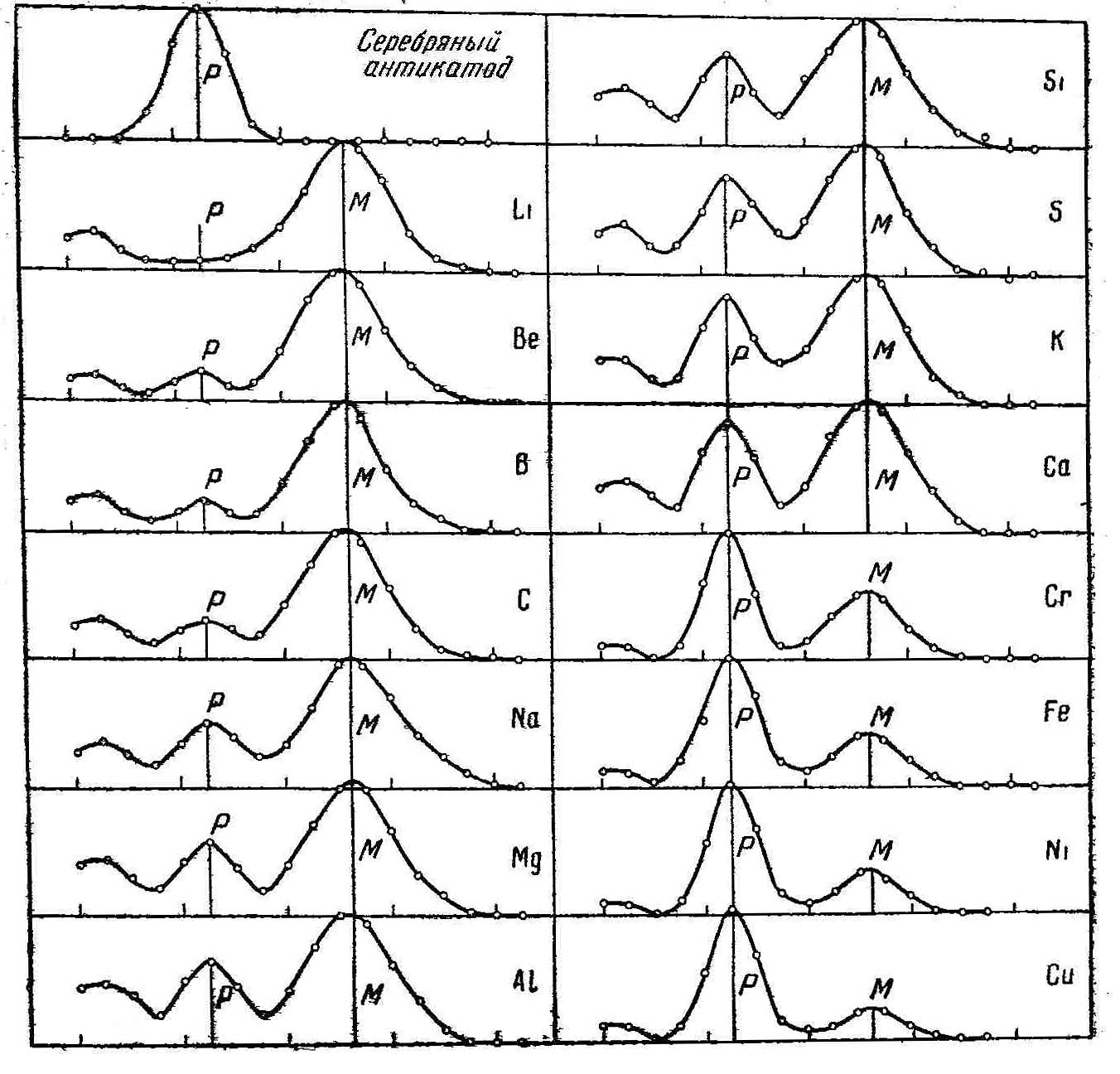На рис. 3 приведены спектры линии K_a. серебряного антикатода (К_a = 0,56267 А), рассеянной под одним и тем же углом различными веществами. Можно установить следующие особенности процесса:

1. Величина смещения не зависит от природы радиатора.

2. E AAQA8wAAAOsFAAAAAA== " stroked="f">

Рис. 3. Эффект Комптона на радиаторах различной природы (Комптон и By).

При возрастании атомного номера радиатора интен­сивность несмещенной линии возрастает, а интенсивность смещенной линии падает. Так, у лития рассеянное излучение практически полностью состоит из смещенной длины волны, а у меди интенсивность смещенной линии невелика по сравнению с интенсивностью линии несмещенной.

§ 2. Элементарная теория эффекта Комптона

Описанные в предыдущем параграфе особенности эффекта Комптона очень легко объяснить, если считать, что излучение имеет корпускулярно-волновую природу, т. е. представляет собою поток фотонов, и что в рассеянии принимают участие не все электроны, а только незначительная часть их, но каждый электрон рассеивает целый фотон. Для того чтобы провести это объяснение до конца, нужно допустить, что фотон обладает не только определенным запасом энергии 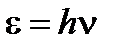, но и определенным количеством движения, т. е. ведет себя, грубо говоря, как движущийся шарик. В таком случае рассеяние фотонов электронами связано с обменом энергии и количества движения при соударениях.

Для того чтобы на основе этого представления произвести расчет смещения длины волны, мы должны прежде рассмотреть некоторые свойства фотона. Фотон как частица обладает, во всяком случае, особыми свойствами, так как он движется со скоростью света. Поэтому формулы классической механики, к движению фотона неприменимы, и нужно пользоваться релятивистскими соотношениями.

Согласно теории относительности масса частицы, движущейся со скоростью v, равна

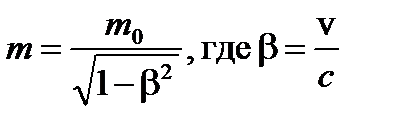
Но так как фотон движется со скоростью с, то (b= 1), и знаменатель предыдущей формулы обращается в нуль. Если бы масса покоя фотона имела конечную величину (т. е. была отлична от нуля), то мы бы получили 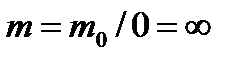. Отсюда следует, что масса покоя фотона обязательно должна быть равной нулю. Этим фотон самым существенным образом отличается от таких частиц, как, например, электроны, которые имеют конечную массу покоя. Вычислим теперь количество движения фотона. Очевидно, что для этой цели мы можем воспользоваться обычной формулой 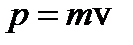. С точки зрения корпускулярно-волновой природы мы можем записать полную энергию фотона как:

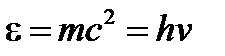(1)

Тогда для частицы, движущейся со скоростью света (v = с), получаем

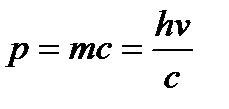(2)

Это и есть искомое выражение для импульса фотона.

Из того факта, что фотон обладает определенным импульсом, следует, что, встречая какое-нибудь препятствие, поток фотонов должен оказывать давление на это препятствие подобно тому, как бомбардировка стенки сосуда молекулами газа в среднем складывается в давление газа. Давление, создаваемое потоком фотонов, и есть световое давление, экспериментально установленное в количественном согласии с формулой (2) знаменитыми работами выдающегося русского физика П. Н. Лебедева.

При этом, как известно, Лебедев доказал не только существование давления света на макроскопические твердые тела, но и с полной несомненностью установил тончайший эффект давления света на газы. Заметим, однако, что, предпринимая свои опыты, Лебедев руководствовался не корпускулярной теорией света, но электромагнитной теорией Максвелла, которая также приводит к выводу о необходимости светового давления и дает для давления формулу, совпадающую с (2). Сам Максвелл, исходя из наглядных представлений Фарадея о силовых линиях электрического поля, рассматривал световое давление как следствие поперечного давления силовых трубок. Уже неоднократно отмечавшейся одним из проявлений двойственности природы света является то, что существование светового давления и его количественное выражение могут быть выведены и из корпускулярной и из волновой картин природы света.

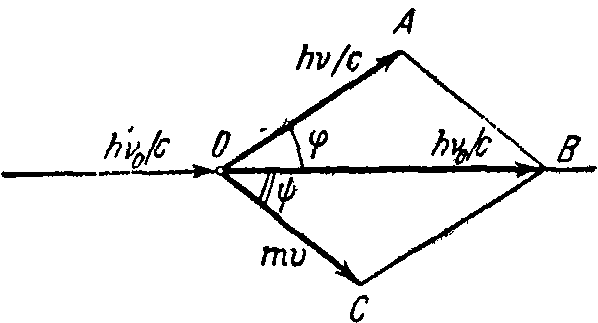Положим теперь, что электрон до соударения покоился, т. е. импульс его до соударения с фотоном был равен нулю; начальный импульс фотона равен 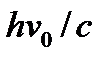. После соударения электрон приобретет импульс mv, где 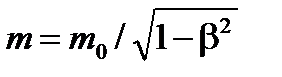, а импульс фотона станет равным .

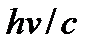Рис. 4.

Применяя законы сохранения энергии и количества движения, т. е. рассчитывая это соударение как удар упругих шаров, получим два уравнения. Из закона сохранения энергии имеем

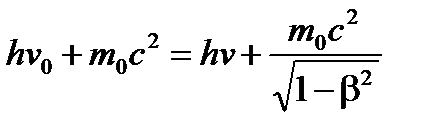(3)

где m₀c² — «энергия покоя» электрона. Обозначив для краткости массу движущегося электрона через m, перепишем (3) так:

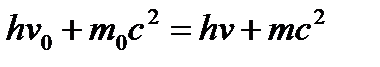(4)

Закон сохранения количества движения дает

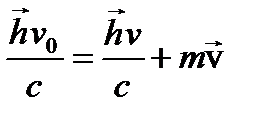(5)

Из уравнений (4) и (5) первое — скалярное, а второе — векторное. Для расчета следовало бы векторное уравнение (5) заменить двумя скалярными уравнениями в проекциях на оси координат. Но мы поступим следующим образом. Векторное уравнение (5) фиксирует треугольник ОАВ (рис. 4.). По формуле элементарной тригонометрии из этого треугольника определяем квадрат стороны АВ, равной по величине mv

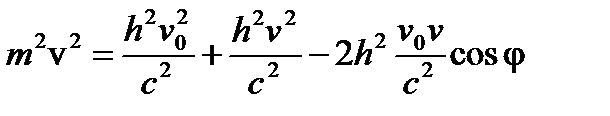
или

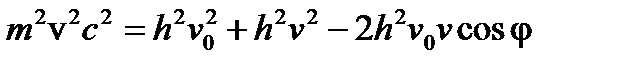(6)

Уравнение (4) перепишем в виде

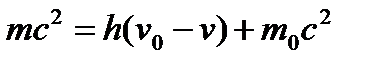
и возведем в квадрат:

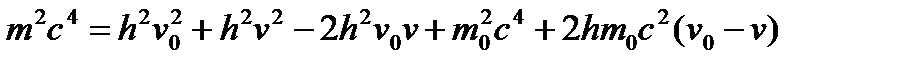(7)

Вычитая (6) из (7), получим

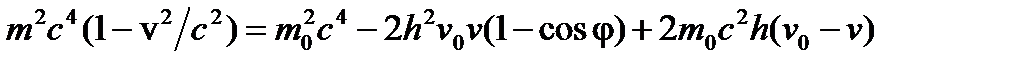(8)

Заметив, что 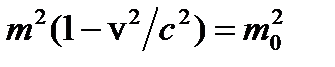и произведя простые преобразования в (8), найдем

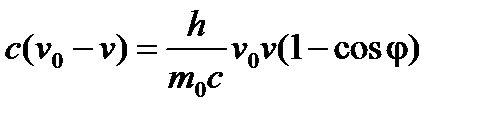(9)

или

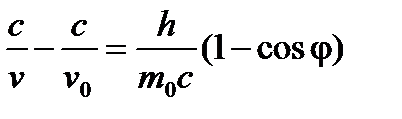(10)

Из (10) легко получим для изменения длины волны формулу, которой чаще: всего пользуются на практике. Принимая во внимание, что 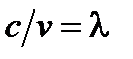и 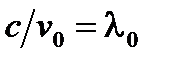, найдем

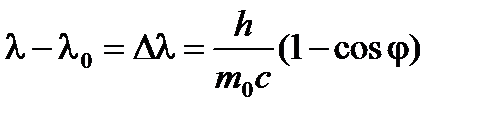(11)

или

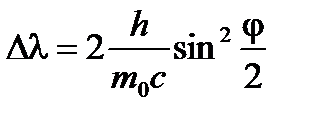(12)

Величина 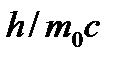, имеющая размерность длины, есть комбинация трех универсальных постоянных; она называется комптоновской длиной волны и обозначается через L:

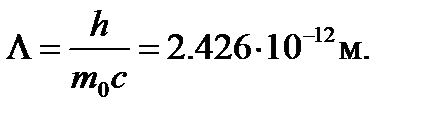(13)

Из формул (11, 12) видно, что для j = 0 Dl = 0, для j = 90° Dl = L и, наконец, для j = 180° Dl = 2L.

Для определения энергии рассеянного фотона представим формулу (10) в виде

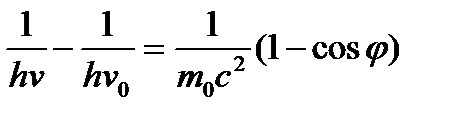(14)

Или

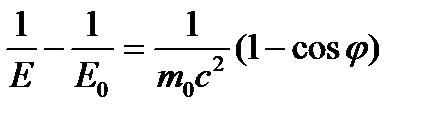
Из последнего равенства следует

(15)

На рис. 2 и 3 вычисленные положения смещенных линий отмечены вертикальными прямыми. Как видно, максимумы экспериментально - измеренных линий очень хорошо совпадают с предсказанными по формуле (11).

Формула (11) показывает, что комптоновское смещение не зависит от длины волны первичного излучения. Поэтому, если бы можно было наблюдать эффект Комптона в видимом спектре, то для крайней фиолетовой части (l=4000 Å) он составлял бы тысячные доли процента основной длины волны; для рентгеновских лучей средней жесткости (l ~ 0,5 Å) он составляет уже около 10%, а для g-лучей величина его порядка самой длины волны.

Нам осталось еще объяснять, почему в рассеянном излучении наряду со смещенной линией наблюдается и несмещенная: из теории, изложенной выше, это не вытекает. Однако при рассмотрении механизма рассеяния мы предполагали, что фотон «соударяется» со свободным электроном. Для легких атомов и для периферических, слабо связанных электронов такое предположение вполне оправдано, так как энергия связи электрона (несколько электрон-вольт) ничтожно мала по сравнению с энергией фотона рентгеновских лучей. Но внутренние электроны, особенно в тяжелых атомах, связаны настолько прочно, что их уже нельзя рассматривать как свободные. Поэтому при «соударении» фотон обменивается энергией и количеством движения с атомом в целом. Так как масса последнего очень велика, то, по закону сохранения количества движения, фотон не передает ему своей энергии и количества движения; следовательно, hv при рассеянии не изменяется.

На основании этих соображений можно качественно оценить соотношение интенсивностей смещенной и несмещенной линий в зависимости от массы атома. В легких атомах все электроны связаны слабо; наоборот, в тяжелых атомах только периферические электроны связаны слабо. Поэтому можно ожидать, что при увеличении атомного номера при одинаковых условиях наблюдения интенсивность смещенной линии будет падать, а интенсивность несмещенной — возрастать. Это и наблюдается на самом деле, как показывает рис. 2.

Из аналогичных соображений следует, что в видимой части спектра эффект Комптона вовсе не может наблюдаться.

Экспериментальная часть

Оборудование

1 XR 4.0 Базовая рентгеновская установка 35кВ 09057-99

1 XR 4.0 Гониометр для рентгеновского аппарата, 35 кВ 09057-10

1 XR 4.0 Сменный модуль с Мо рентгеновской трубкой 09057-60

1 Диафрагменная трубка d = 1 мм 09057-01

1 Диафрагменная трубка d = 2 мм 09057-02

1 Многоканальный анализатор 13727-99

1 Рентгеновский детектор энергии 09058-30

1 XR 4.0 XRED кабель 50 см 09058-32

1 Экранированный кабель, BNC, L = 750 мм 07542-11

1 Комптон-крепление для 35 кВ рентгеновского аппарата 09057-04

1 Программное обеспечение для многоканального анализатора 14452-61

ПК, Windows 98 или выше

Рис. 1:Установка P2546001

Задания

Рис. 2: Соединения в области экспериментов

1. Калибровка полупроводникового детектора энергии

2. Определение энергии фотонов W- L_α линии, рассеянных акриловым стеклом в зависимости от угла рассеяния.

3. Сравнение измеренных значений энергии линий рассеяния с расчетными значениями энергии.

4. Расчёт длины волны Комптона электронов и сравнение этого значения с соответствующим значением рассеяния на 90°.

Рис. 3: Подключение на внешней панели XR 4.0 экспертного рентгеновского аппарата к МКА

Установка и ход работы

Настройка (рис. 1)

- Привинтите переходное кольцо к входной трубе детектора энергии.

- Подключите сигнальный и питающий кабели к соответствующим портам детектора с помощью прямоугольных разъёмов.

- Подключите сигнальный и питающий кабели от МКА в соответствующие соединения в экспериментальной камере рентгеновского аппарата (сигнального кабеля: красное, кабеля питания: зеленое (рис 2).).

Рис. 4: Настройка гониометра

- Подключите внешние порты X RED рентгеновского аппарата (сигнальный кабель красный, зеленый сетевой кабель, рис. 3.) к многоканальному анализатору (МКА).

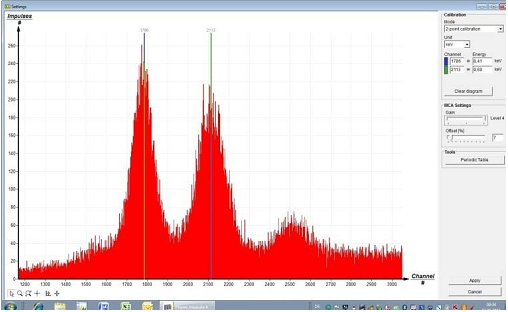
Рис. 5: калибровка многоканального анализатора

Подключите сигнальный кабель через экранированный BNC-кабель к "Input" порту МКА и кабель питания к "X-Ray Energy Det." порту МКА.

- Закрепите детектор энергии в держателе поворотного рычага гониометра. Уложите два кабеля достаточной длины так, чтобы гониометр мог поворачиваться свободно по всему поворотному диапазону.

- Подключите с помощью кабеля USB многоканальный анализатор и компьютер.

- Вставьте диафрагменную трубку с 2-мм-отверстием.

- Приведите блок гониометра и детектор на свои конечные положения на право.