Вопрос 31. Явление самоиндукции. Полный магнитный поток. Индуктивность контуров. ЭДС самоиндукции. Экстратоки замыкания и размыкания

Самоиндукция – явление возникновения ЭДС индукции в цепи в результате изменения тока в этой цепи. Магнитное поле тока создаёт магнитный поток Ф_m сквозь поверхность S, ограниченную самим контуром: Ф_m=ò_(S)B_ndS.

Индуктивность L – численно равна магнитному потоку, охватываемому контуром, когда сила тока в контуре равна единице. Ф_m=LI.

Соленоид – цилиндрическая катушка, состоящая из большого числа витков проволоки, образующая винтовую линию.

Расчёт индуктивности соленоида (l – длина, S – площадь поперечного сечения, N – число витков) – L=k*((m₀mN²S)/l)=km₀mn²V, где n=N/l – число витков на единицу длины, V=Sl – объём соленоида, k – коэффициент размагничивания (зависит от отношения длины l соленоида к диаметру d его витков \\k – таблица\\), m₀ – магнитная постоянная, m - относительная магнитная проницаемость среды.

ЭДС самоиндукции e_C – определяется по закону Фарадея: e_C=-d(Ф_m)/dt=- d(LI)/dt

Магнитный поток Ф_m – в магнитной цепи как сила тока в электрической цепи

При всяком изменении силы тока в проводящем контуре возникает э. д. с. самоиндукции, в результате чего в контуре появляются дополнительные токи, называемые экстратоками самоиндукции. Экстратоки самоиндукции, согласно правилу Ленца, всегда направлены так, чтобы препятствовать изменениям тока в цепи, т. е. направлены противоположно току, создаваемому источником. При выключении источника тока экстратоки имеют такое же направление, что и ослабевающий ток. Следовательно, наличие индуктивности в цепи приводит к замедлению исчезновения или установления тока в цепи.

Вопрос 32. Гармонические колебания, их характеристики. Пружинный, физический маятники. Сложение колебаний.

Затухающие колебания

Колебательная система взаимодействует с окружающей средой. На систему действует 2 силы.

1. 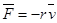(1) сила сопротивления

При незначительных отклонениях от равновесия, величину Fс можно считать пропорциональной скорости системы. 2.Помимо этого, на систему действует квазиупругая сила:

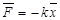
По второму закону Ньютона: ma=F+Fc

ma=-rV – kx-диф.ур-ние затух.кол-ний

mx"= - rx'-kx

mx"+ rx'+ kx=0

x"+(r/m)x'+(k/m)x=0 (2)

Уравнение (2) можно рассматривать, как закон движения системы, совершающий затухающие колебания.

k/m=ω²; r/m=2δ

ω0²- собственная циклическая частота кол-ний.

δ- коэффициент затухания [δ]=[cˉ¹]

x"+2δx'+ωо²х=0 (2') – дифференциальное уравнение второго порядка.

ω0-собственная цикл.частотакол-ний

решением данного ур-ния и будет закон затух.колебония:

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.

В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.

Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

и не зависит[1] от амплитуды и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.