Характеристики обнаружения при некогерентном накоплении сигнала

На выходе некогерентного накопителя формируется случайная величина

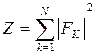
Ее закон распределения определяется:

- во-первых, законом распределения слагаемых 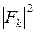, т.е. законом распределения смеси сигнала и шума на выходе детектора, который является экспоненциальным, как закон распределения квадрата модуля нормально распределенной случайной величины ;

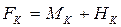- во-вторых, числом слагаемых N;

- в-третьих, степенью коррелированности слагаемых, которая зависит от относительной интенсивности m и междупериодной кор­релированности r_с сигнала.

В общем случае закон распределения суммы (экспоненциально распределенных случайных величин есть так называемое хи-квадрат распределение

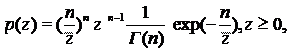
число степеней, свободы которого 2n зависит от числа и степени коррелированности слагаемых. Этот закон распределения является двухпараметрическим 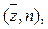причем параметр n определяет соотношение квадрата среднего значения и дисперсии случайной величины z:

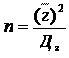
Значению n = 1 соответствует экспоненциальное распределение. При увеличении параметра n > 1 происходит нормализация закона распределения (рис. 8.6).

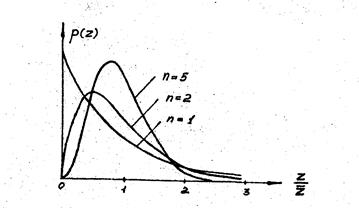
Рис. 8.6 Нормализация хи-квадрат распределения с ростом параметра n

Проследим на физическом уровне эволюцию закона распределе­ния случайной величины z, т.е. эволюцию параметра n при из­менении числа слагаемых N, относительной Интенсивности m и междупериодной коррелированности r_с сигнала. При независи­мых (некоррелированных) слагаемых, что характерно для случая отсутствия сигнала (m = 0) и наличия только некоррелированного от периода к периоду шума или для случая наличия смеси шума и быстро флуктуирующего сигнала (r_с = 0) произвольной интенсивности m параметр n (половина числа степеней свободы хи-квадрат распределения) определяется числом слагаемых:

n = N, m = 0, r_с = 0,

т.е. происходит нормализация закона распределения случайной величины z по мере увеличения числа слагаемых, что соответствует центральной предельной теореме Теории вероятностей (теореме Ляпунова). При сильно коррелированных слагаемых, что характерно для случая сильного (m >> N) медленно флуктуирующего (r_с ® 1) сигнала, закон распределения суммы определяется за­коном распределения слагаемых, т.е. сохраняется экспоненциальным:

n = 1, m >> N, r_с ® 1.

Рассмотренные частные случаи ''поглощаются" следующим соотношением, определяющим эволюцию параметра n при изменении числа слагаемых N, относительной интенсивности m и междупериодной коррели­рованности r_с сигнала:

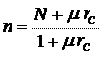
При этом вероятности ложной тревоги и правильного обнаружения оп­ределяются следующими выражениями,

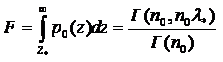
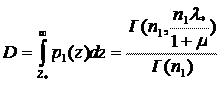
где

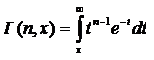– неполная гамма-функция,

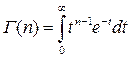– полная гамма-функция,

n₀ = N – половина числа степеней свободы хи-квадрат распределения в отсутствие сигнала,

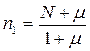– половина числа степеней свободы хи-квадрат распределения при наличии медленно флуктуирующего сигнала (r_с ® 1),

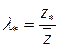– нормированный порог.

Нормированные неполные гамма-функции табулированы и ими необходимо пользоваться при расчете и анализе характеристик обнаружения. На рис. 8.7 и 8.8 показаны рассчитанные характеристики обнаружения при некогерентном накоплении медленно (r_с ® 1) и быстро (r_с = 0) флуктуирующего сигнала, на основании которых можно сделать следующие выводы.

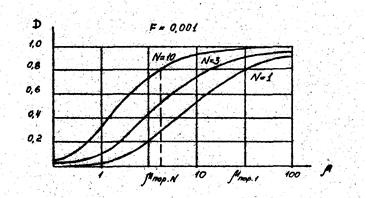
Рис. 8.7. Характеристики обнаружения при некогерентном накоплении медленно флуктуирующего сигнала.

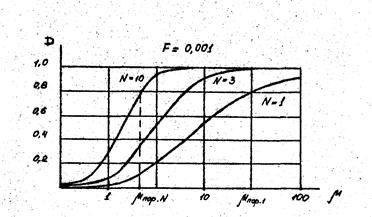
Рис. 8.8 Характеристики обнаружения при некогерентном накоплении быстро флуктуирующего сигнала (r_с=0).

Во-первых, некогерентное накопление является эффективной опе­рацией обработки сигнала, улучшающей характеристики обнаружения системы, как при медленно (r_с ® 1), так и при быстро (r_с = 0) флуктуирующем сигнале.

Во-вторых, эффективность некогерентного накопления медленно флуктуирующего сигнала, определяемая как выигрыш в пороговом сигнале

,

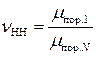уступает эффективности когерентного накопления такого же сигнала. Если эффективность когерентного накопления определяется числом сиг­налов

,

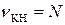то эффективность некогерентного накопления растет медленнее, чем увеличивается число слагаемых

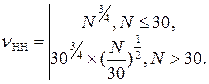
Эффективность, выраженная в децибелах, определяется следующим обра­зом:

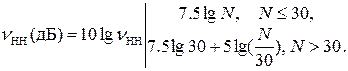
Это означает, что при некогерентном накоплении имеют место потери по с равнению с когерентным накоплением

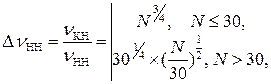
которые составляют в децибелах

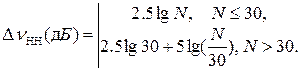
Например, при N=16 эффективность некогерентного накопления 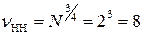, а потери при некогерентном накоплении 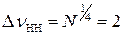, т.е. составляют 3 дБ.

В-третьих, в области надпороговых сильных сигналов ( 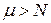) некогерентное накопление медленно флуктуирующего сигнала оказывает­ся эффективнее когерентного накопления (рис. 8.9). Основой этого феномена является диаметральное различие законов распределения когерентно и некогерентно накопленного шума ( 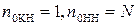) и одинаковость законов распределения когерентно и некогерентно накопленной смеси сильного сигнала и шума 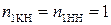. При этом вероятность правильного обнаружения при когерентном и некогерентном накоплении сильных сигналов оказываются одинаковыми ( 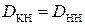), а вероятность ложной тревоги при когерентном накоплении оказывается больше, чем при некогерентном накоплении ( 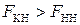), т.к. экспоненциальное распределение ( 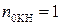) в области надпороговых сигналов убывает медленнее, чем хи-квадрат распределение с большим числом степеней свободы 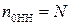(рис. 8.10).

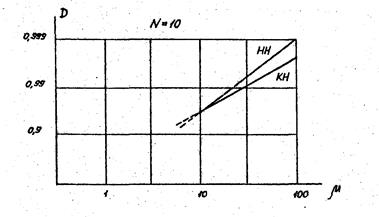
Рис. 8.9 Сравнение характеристик обнаруже­ния когерентного (КН) и некогерентного (НН) накопления в области надпороговых сильных (m>N) и медленно флуктуирующих сигналов.

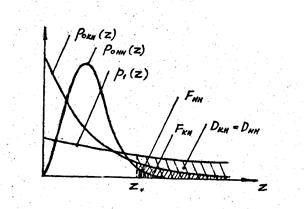
Рис. 8.10. Пояснение преимуществ некогерентного накопления по сравнению с когерентным в случае сильного медленно флуктуирующею сигнала.