Описание экспериментальной установки

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

НАЦИОНАЛЬНЫЙ МИНЕРАЛЬНО-СЫРЬЕВОЙ УНИВЕРСИТЕТ «ГОРНЫЙ»

Кафедра общей и технической физики

Общая физика

ВОЛНОВАЯ ОПТИКА

Поляризация четвертьволновыми пластинами

Методические указания к лабораторной работе

САНКТ-ПЕТЕРБУРГ

УДК 535.41/42 + 535.5 (075.80)

Физика. ПОЛЯРИЗАЦИЯ ЧЕТВЕРТЬВОЛНОВЫМИ ПЛАСТИНАМИ: Методические указания к лабораторной работе / Сост.: А.С. Мустафаев, А.Ю. Грабовский. Национальный минерально-сырьевой университет «Горный». СПб, 2016. 12 с.

В методических указаниях к лабораторной работе «ПОЛЯРИЗАЦИЯ ЧЕТВЕРТЬВОЛНОВЫМИ ПЛАСТИНАМИ» сформулированы: теория, методические указания и алгоритм выполнения работы.

Лабораторная работа дает возможность студентам исследовать различные виды поляризованного света, определить степень поляризации лазерного излучения и провести экспериментальную проверку закона Малюса. Основная задача - овладеть техникой и методикой проведения эксперимента, а также приемами обработки его результатов и оформления заключительного отчета.

В зачетной работе практикума студент должен продемонстрировать умение в устной и письменной форме, логически верно и аргументировано защищать результаты своих исследований.

Методические указания к лабораторной работе предназначены для студентов всех специальностей и направлений подготовки бакалавриата и магистратуры Национального минерально-сырьевого университета «Горный».

Научный редактор проф. А.С. Мустафаев

Ó Национальный минерально-сырьевой университет «Горный», 2016 г.

ПОЛЯРИЗАЦИЯ ЧЕТВЕРТЬВОЛНОВЫМИ ПЛАСТИНАМИ

Теоретические сведения

Видимый свет, как известно, представляет собой электромагнитные волны с длинами волн от 4×10^–7 м (фиолетовый) до 7×10^–7 м (красный). В электромагнитной волне векторы напряженности электрического поля 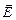и магнитного поля взаимно перпендикулярны и одновременно перпендикулярны направлению распространения волны (рис. 1). Плоскость, проведенную через направления 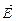и , называют плоскостью колебаний электрического вектора.

Для полной характеристики волны задают ее длину l, модули векторов 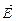и и ориентацию в пространстве плоскости колебаний электрического вектора. Если для некоторого пучка света плоскость колебаний электрического вектора не изменяет положение в пространстве, то такой свет называют линейно-поляризованным.

Естественный или неполяризованный свет можно рассматривать как наложение многих электромагнитных волн, распространяющихся в одном и том же направлении, но со всевозможными ориентациями плоскостей колебаний. Таким образом, для неполяризованного света нельзя указать даже плоскость преимущественного расположения вектора напряженности электрического поля 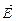. Все ориентации этого вектора равновероятны. Если же имеется какое-либо преимущественное направление ориентации вектора 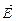, то световой пучок называют частично-поляризованным.

Если в световом пучке вектор 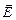имеет составляющие как по оси х, так и по оси у, причем и , где w – частота световой волны, то в каждый момент времени t эти составляющие складываются. Результирующий вектор, оставаясь постоянным по величине, вращается с частотой w, а его конец описывает окружность. В этом случае говорят, что свет имеет круговую поляризацию.

Если составляющие вектора 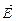по осям х и у колеблются с одинаковыми частотами, но имеют либо разные амплитуды, либо разность фаз колебаний отличается от 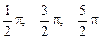и т.д., то конец электрического вектора будет описывать эллипс и в этом случае говорят об эллиптической поляризации светового пучка. Таким образом, имеется пять типов поляризованного света:

· естественный или неполяризованный свет;

· частично поляризованный свет;

· линейно или плоско поляризованный свет;

· свет, поляризованный по кругу;

· эллиптически поляризованный свет.

Пусть на поляризатор падает линейно-поляризованное излучение интенсивностью I₀ (рис. 2). Разложим вектор 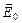на две составляющие, лежащие в главной плоскости поляризатора: Е_|| = Е₀cosj, и перпендикулярную составляющую E_^ = E₀sinj, где j – угол между плоскостью колебаний электрического вектора, падающего на поляризатор излучения, и главной плоскостью поляризатора. Поскольку поляризатор пропускает излучение только с составляющей вектора 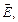лежащей в главной плоскости, то выходящее излучение имеет интенсивность

I ~ < E_||² > = < E₀² cos²j >,

здесь угловые скобки обозначают, усреднение по времени. Учитывая, что интенсивность падающего излучения I₀~ <E₀²>, получим

I = I₀cos²j. (1)

Последнее соотношение называют законом Малюса.

Если направить на поляризатор естественное (неполяризованное) излучение, в котором все ориентации вектора напряженности равновероятны (т.е. возможны любые значения j), то проводя усреднение по углу j в соотношении (1) получим I = 0,5 I_ест. Таким образом, при прохождении через поляризатор естественное излучение становится линейно-поляризованным, но убывает по интенсивности вдвое.

Для количественной оценки степени поляризацииизлучения применяется соотношение

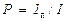. (2)

Частично поляризованное излучение понимается как смесь линейно-поляризованного и неполяризованного излучений. Тогда I – полная интенсивность, I_п – интенсивность линейно-поляризованного компонента. Очевидно, , где I_н – интенсивность неполяризованного компонента. Поскольку 0 < I_н< I, то степень поляризации может меняться в пределах 0 < Р< 1.

Если направить частично-поляризованное излучение на поляризатор и вращать устройство, меняя угол между главной плоскостью поляризатора и преимущественным направлением вектора 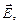то интенсивность прошедшего излучения будет меняться от максимального значения I_max до минимального I_min. В первом положении поляризованный компонент проходит полностью, а неполяризованный уменьшается по интенсивности вдвое:

I_max = I_п + I_н / 2. (3)

Во втором положении, которое отличается по углу от первого на 90°, поляризованный компонент, согласно закону Малюса, полностью задерживается, а неполяризованный по-прежнему умень­шается вдвое:

I_min = I_н/ 2. (4)

Складывая и вычитая уравнения (3) и (4), имеем 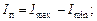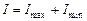. Подставляя последние соотношения в (2) получим формулу для расчета степени поляризации при обработке экспериментальных данных:

Р = (I_max – I_min) / (I_max + I_min). (5)

Способ получения эллиптически поляризованного излучения. Допустим, что из двоякопреломляющего кристалла вырезана пластинка таким образом, что оптическая ось лежит в плоскости среза. Допустим далее, что излучение падает на пластинку перпендикулярно плоскости среза. В этом случае колебания электрического вектора, как в обыкновенной волне ( ), так и в необыкновенной ( ) совершаются согласованно (когерентно). И в дальнейшем будем индексом о - обозначать обыкновенную волну; индексом е – необыкновенную.

Направления электрических векторов обыкновенного и необыкновенного лучей взаимноперпендикулярны. И эти лучи распространяются в одном направлении, но с разными скоростями. В связи с этим, при прохождении через пластинку между ними возникает разность хода:

DL = (n_o – n_e)d, (6)

где d – толщина кристаллической пластинки; n_o и n_e показатели преломления обыкновенного и необыкновенного лучей.

Как уже отмечалось, при наличии разности хода волны могут интерферировать только в том случае, если они когерентны. Если падающее на кристалл излучение не поляризовано, о - и е-волны испускаются разными группами атомов (не согласованно), поэтому волны не когерентны. Если же на кристалл падает линейно-поляризованный свет, то волна разделяется между о- и е-волнами в пропорции, которая зависит от ориентации плоскости колебаний. Поэтому возникающие о- и е-компоненты когерентны и способны интерферировать.

Из теории сложения колебаний известно, что при сложении взаимно перпендикулярных колебаний одинаковой частоты конец результирующего вектора движется по эллипсу (рис. 3):

x²/E_о² – (2xy/E_оE_е) cos (dj) + y²/ E_е² = sin²(dj),

где dj – сдвиг фаз колебаний на выходе из пластинки кристалла; x и y – координаты конца результирующего вектора 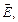x º E_x, y º E_y.

Нас интересует случай, когда эллипс ориентирован своими полуосями по осям Оx и Оy (Оу лежит в главной плоскости кристалла), при этом E_oи E_eявляются полуосями эллипса. Это наблюдается, если выполнено условие для разности фаз: , k = 0, 1, 2, … Уравнение эллипса преобразуется при этом к виду

E_x²/E_о² + E_y²/E_e² = 1.

Разность фаз колебаний связана с разностью хода лучей: dj = 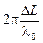. Используя (6), получим

d(n_o – n_e) = ±(λ₀/4 + kλ). (7)

Здесь знак плюс соответствует отрицательным кристаллам (n_o> n_e), знак минус – положительным кристаллам (n_o < n_e). Таким образом, если толщина пластины, вырезанной вдоль оптической оси, удовлетворяет условию (7), результатом будет эллиптическая поляризация выходящего излучения. Такая пластина носит название четвертьволновой или пластины λ/4.

Способ полученияциркулярной (круговой) поляризации излучения. Эллипс превращается в окружность при равенстве полуосей эллипса, т.е. E_o = E_e º E. Этого достигают, ориентируя четвертьволновую пластину оптической осью под углом a = 45° к плоскости колебаний падающего излучения. При этом компоненты результирующего вектора 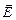удовлетворяют уравнению окружности: E_x² + E_y² = E². Заметим, что при a = 0° и a = 90° из четвертьволновой пластины выходит плоскополяризованное излучение (электрический вектор 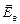в первом случаеи во втором).

Описание экспериментальной установки

Общий вид и схема установки представлены на рис. 4 и 5 соответственно.

Рис. 4

Рис. 5

В состав установки входят: He-Ne лазер 1 мощностью 1,0 мВт (используется как источник света), оптическая скамья 2; поляризатор 3, четвертьволновая (λ/4) пластина 4, анализатор 5, фотоэлемент 6; цифровой мультиметр 7, используемый для измерения силы фототока. Для отсчета углов поворота элементы 3, 4 и 5 установлены во вращающемся держателе с радиально нанесенными делениями.

Излучение лазера частично-поляризовано. Для получения различных видов поляризации количество элементов (3, 4, 5) на оптической скамье может варьироваться. На рис. 5 представлена схема эксперимента по изучению эллиптической и круговой поляризации. Лазерное излучение проходит через поляризатор 3, четвертьволновую пластину 4, направляется на анализатор 5 и затем попадает на фотодетектор 6. Фототок, пропорциональный интенсивности света, прошедшего через анализатор, измеряется цифровым мультиметром 7, работающим в режиме амперметра.

Порядок выполнения работы

Задание 1. Исследование степени поляризации лазерного излучения

1. Проверить установку в соответствии со схемой. На оптической скамье установить лазер 1, анализатор 5 и фотодетектор 6, сняв с оптической скамьи поляризатор 3 и четвертьволновую пластинку 4.

2. Поворачивая анализатор вокруг горизонтальной оси в диапазоне углов ±90^о с шагом 10^о, наблюдать за показаниями мультиметра. Если фототок, регистрируемый прибором, при вращении анализатора изменяется от некоторого минимального до максимального значения, то это, означает, что излучение частично-поляризовано. Результаты измерений фототока в зависимости от угла поворота анализатора записать в таблицу 1.

Таблица 1

φ, град.	-90	…	-10		+10	…	+90
I, мА

3. Рассчитать степень поляризации частично-поляризованного света Р по формуле (5), используя максимальное и минимальное значение силы фототока.

4. По полученным экспериментальным данным построить лепестковую диаграмму .

Задание 2. Изучение линейно-поляризованного света. Проверка закона Малюса

1. Получить линейно-поляризованное излучение. Для этого ввести в оптический канал поляризатор 3. «Ноль» на шкале поворотных элементов, в которых закреплены поляризатор и анализатор, совмещен с положением их максимального пропускания. Поэтому, согласно закону Малюса, на круговой шкале поляризатора 3 должен быть установлен угол 0^о.

2. Поворачивая анализатор вокруг горизонтальной оси от 0^о до ±90^о, фиксировать через каждые 10^о угол поворота φ и силу фототока I (табл. 2). Если фототок изменяется от нуля до максимального значения, то это, означает, что излучение линейно-поляризовано.

Таблица 2

φ, град.	-90	…	-10		+10	…	+90
I, мА
I/I0
cos2 φ

3. Проделать необходимые вычисления I/I₀ и cos² φ, занося результаты в табл. 2.

4. Построить лепестковую диаграмму с отображением двух графиков на одной диаграмме: экспериментальные данные и функцию I₀cos²φв зависимости от угла поворота.

5. Построить график I/I₀=f (cos² φ). Проанализировать график и сделать вывод относительно выполнения закона Малюса.

Задание 3. Изучение эллиптической поляризации

1. Ввести в оптический канал четвертьволновую пластину 4, согласно рис. 5.

2. Измерить силу фототока в зависимости от угла φположения анализатора, через каждые 10^о в диапазоне ±90^о (табл. 3)

Таблица 3

φ, град.	-90	…	-10		+10	…	+90
I, мА

3. По полученным экспериментальным данным построить лепестковую диаграмму . Убедиться в том, что сила тока меняется в пределах от I _max до I _min, сделать вывод о характере поляризации.

4. Рассчитать отношение полуосей эллипса поляризации:

.

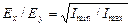Задание 4. Исследование круговой поляризации

1. Получить излучение круговой поляризации. Для этого поворачивать пластину «λ/4» на небольшие углы (порядка 10°) и в каждом положении вращать анализатор, наблюдая изменение интенсивности от I _max до I _min. То положение, при котором это изменение будет наименьшим, соответствует углу 45° между плоскостью поляризации излучения и оптической осью четвертьволновой пластины.

2. Записать значения фототока в зависимости от угла поворота анализатора в таблицу 4.

Таблица 4

φ, град.	-90	…	-10		+10	…	+90
I, мА

3. По полученным экспериментальным данным построить лепестковую диаграмму . Убедиться в том, что полученная поляризация действительно соответствует круговой.

Контрольные вопросы

1. Что такое естественный свет?

2. Что называется плоскостью пропускания (или главной плоскостью поляризатора)?

3. Что такое поляризованный свет?

4. Что такое линейно-поляризованный свет?

5. Что такое частично-поляризованный свет?

6. По какой формуле следует записать интенсивность света после прохождения поляризатора, если на поляризатор падал линейно-поляризованный свет?

7. Как определить характер поляризации света, падающего на поляризатор?

8. По какой формуле определяется интенсивность частично-поляризованного света?

9. Чему равна степень поляризации частично-поляризованного света?

10. Чему равна интенсивность линейно-поляризованного света, прошедшего через поляризатор, если на поляризатор падал частично-поляризованный свет.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Савельев И.В. Курс общей физики. СПб, М.: Лань, 2009. Т.2-3. 10-е изд.

2. Фриш С.Э. Курс общей физики. / Фриш С.Э., Тиморева А.В. СПб, М.: Лань, 2009. Т.2-3. 10-е изд.

3. Яворский Б.М. Справочник по физике / Б.М.Яворский, А.А.Детлаф. М.: ОНИКС, Мир и Образование,2008, 8-е изд.

СОДЕРЖАНИЕ

Теоретические сведения. 3

Описание экспериментальной установки. 8

Порядок выполнения работы.. 9

Контрольные вопросы.. 12

БИБЛИОГРАФИЧЕСКИЙ СПИСОК.. 13